Добавил:

Justeeeek100500 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный университет Львовская политехника

Предмет:

Вища геодезія

Файл:

Лаби методичка.pdf

Скачиваний:

Добавлен:

28.06.2022

Размер:

1.51 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

B. Порядок розв’язування великого сфероїдного трикутника за відомими сторонами

При розв΄язуванні великих трикутників, отриманих в результаті вимірювання сторін радіогеодезичними або супутниковими навігаційними системами (GPS), потрібно визначити азимути виміряних сторін. Для цього необхідно знати кути між сторонами, тобто розв΄язати сфероїдний трикутник за відомими сторонами.

Постановка задачі. Задано (рис.) сторони а, в, с сфероїдного трикутника, геодезичні широти BA, BB, BC його вершин і середню широту розміщення трикутника Bm. Необхідно визначити кути A, B, C цього трикутника.

Розв΄язок задачі виконують у такій послідовності:

1.Обчислення за формулою (23) сферичного надлишку ε та за формулами (17) поправок δ в кути за сфероїдність.

2.Обчислення сферичних кутів за формулами (26).

3.Обчислення сфероїдних кутів за формулами (16).

Приклад розв’язування великого сфероїдного трикутника

за відомими сторонами

Вихідні дані

425340.808м

49050’11”

752860.142м

50033’01”

635221.881м

54021’10”

51000’25”

1.Обчислення поправок в кути за сфероїдність трикутника

6378245м

6390748м

2.45534·10-14

a(1-e2)

6335553

6391011

2.45494·10-14

6.69342·10-3

6392388

2.45283·10-14

6372884м

6391179

2.45534·10-14

6373671

6382670

δA

0.015”

6377791

2.53·10-3

δB

0.006

6374173

684.437

δC

-0.043

2.Обчислення сферичних кутів трикутника

3.818187867

sin(po-ao)

0.075346901

tg2(Aсф/2)

0.096074028

6.758254571

sin(po-bo)

0.024102198

tg2(Bсф/2)

0.938908976

5.702242609

sin(po-co)

0.042522593

tg2(Cсф/2)

0.301645813

8.139342524

sin(po)

0.141581005

Елементи

Значення

Назва

Сферичні кути

формул

вершини

Aoсф/2

17.22124630

34026’32.973”

Boсф/2

44.09721465

88011’39.946”

Coсф/2

28.77659937

57033’11.515”

3. Перехід від сферичних кутів до сфероїдних

Назва

Сферичні кути

δі

Сфероїдні кути

верш.

34026’32.973”

0.015”

34026’32.988”

88011’39.946”

0.006”

88011’39.952”

57033’11.515”

-0.043”

57033’11.475”

Розв’язування головних геодезичних задач на поверхні земного еліпсоїда за методами Гаусса (із середніми аргументами) та методом Рунге-Кутта

Загальні положення

До головних геодезичних задач відносять пряму та обернену геодезичні задачі, які в залежності від вибору поверхні відносності розв’язують на сфері, еліпсоїді чи в просторі. Розглянемо порядок розв’язування названих задач на поверхні еліпсоїда Красовського.

Параметри еліпсоїда Красовського: a = 6378245 м ; e2 = 0.006693421623.

1.Розв'язування прямої і оберненої геодезичних задач на поверхні еліпсоїда на основі методу із середніми аргументами

(формул Гаусса)

1.1. Пряма геодезична задача

Алгоритм розв’язку

i = 0,

bi = 0, ai = 0,

li = 0.

= B +

= A +

;

bi+1

= scos Am

i 2

+ l

i 2

ï1 + a

ï,

ssin A

i 2

li+1 =

í1 +

ý,

i cos B i

i 2

i 2 ü

i+i

i+1

= l

sin Bm

.í1 +

ý.

i+1

B +

bi+1

i+1

= A +

ai+1

i = i + 1,

якщо

Bmi +1 - Bmi

Ami +1 - Ami

< 0.001",

то тоді остаточно знаходять

< 0.0001"

B = B + bi

L = L + li ,

A = A + ai .

У випадку невиконання поставлених умов повторюють обчислення за формулами, які виділені у прямокутнику.

Вхідні дані:

B1 = 50o , L1 = 24o , A1 = 45o , s = 60000 м.

Позначен	Числові значення
ня
Bmo	50o
Amo	45o
b1	6.657144 10-3
a1	7.911677 10-3
l1	1.032793 10-2
Bm1	50o11’26.56”
Am1	45o13’35.95”
b2	6.6306144 10-3
a2	7.9967807 10-3
l2	1.0409943 10-2
Bm2	50o11’23.831”
Am2	45o13’44.727”
b3	6.63033218 10-3
a3	7.99690367 10-3
l3	1.04102177 10-2
Bm3	50o11’23.8021”
Am3	45o13’44.740”
b4	6.63033178 10-3
a4	7.99690187 10-3
l4	1.04102165 10-2
Bm4	50o11’23.8020”
Am4	45o13’44.740”
B2	50o22’47.6041”
L2	24o35’47.2613”
A2	225o27’29.479”

1.2. Обернена геодезична задача

Алгоритм розв’язку

B2 - B1 = b, L2 - L1 = l,

(B1 + B2 ) = Bm .

Mm =

a(1 - e2 )

Nm =

(1 - e2 sin2 Bm )

s cos A

= Q = bM

ì1 -

l2 sin 2

ü,

m í

ssin A

= P = lN

cos B

ì1 -

2 sin 2 Bm

ü.

m í

tgAm ' = QP .

В залежності від знаків P і Q знаходимо азимут Am .

a = l sin B	ì1 +	l 2	sin2	Bm	+	b2	+	l2	ü,

	m í		24	12			12		ý
	î								þ

A1 = Am - a2 , A2 = Am + a2 ± 180o .

s = Qcos A	+ P sin A = Q2	+ P2 .
m	m

Вхідні дані

B1 = 50o , B2 = 50o 22'47.6041"

L1 = 24o , L2 = 24o 35'47.2613".

Позначен	Числові значення
ня
b	6.63033178 10-3
l	1.04102166 10-2
Bm	50o11’23.80205”
Mm	6373274.198
Nm	6390878.516
P	42595.70715
Q	42256.42824
Am’	45o13’44.7397”
Am	45o13’44.7397”
a	7.99690851 10-3
A1	44o59’59.999”
A2	225o27’29.480”
s	60000.000

2.Розв'язування прямої геодезичної задачі чисельним методом (формули Рунге-Кутта)

Алгоритм розв’язку Алгоритм розв'язування приведений для випадку, коли можна

виконати інтегрування зразу по всій довжині геодезичної лінії (до 100 км) без поділу її на частини, тобто h=s.

M (B) =

a(1 - e2 )

;

N(B) =

;

R =

M (B)N (B).

(1 - e2 sin 2 B)3/ 2

(1 - e2 sin 2 B)1/ 2

k 1

= h cos( A1 ) ,

= h

sin( A1 )

, k 1

= k

1 sin B .

M (B1 )

N(B1 ) cos B1

cos( A + 0.5k

1 )

sin( A + 0.5k 1 )

= h

k2 = h

= k2

sin( B1 + 0.5k1 ).

M (B + 0.5k

1 )

N(B + 0.5k 1 ) cos(B + 0.5k 1 )

	3		cos( A				+ 0.5k 2 )						3							sin( A			+ 0.5k			2 )							3	3		2
k1		= h		1					3			,	k2 = h									1			3						,		k3	= k2 sin( B1 + 0.5k1		).
k1		= h	M	(B			+ 0.5k 2 )					,	k2 = h			N (B				+	0.5k	2 ) cos(B					+ 0.5k 2 )				,		k3	= k2 sin( B1 + 0.5k1		).
				1					1									1			1				1					1
	4		cos( A + k 3 )									4					sin( A + k						3 )						4			4			3
k1		= h		1					3	, k2			= h								1	3						, k3		= k2			sin( B1 + k1 ).
k1		= h	M (B + k						3 )	, k2			= h	N(B + k						3 ) cos(B + 0k 3 )								, k3		= k2			sin( B1 + k1 ).
				1				1									1		1				1	1
B		= B +		1		(k		(1)	+ 2k			(1)	+ 2k		(1)		+ k		(1) ),
B	2	= B +				(k		(1)	+ 2k		2	(1)	+ 2k		(1)		+ k		(1) ),
	2	1		6			1				2			3				4
				6
L		= L +		1	(k			(2)	+ 2k			(2)	+ 2k		(2)		+ k			(2)	),
L	2	= L +			(k				+ 2k		2		+ 2k				+ k		4		),
	2	1		6			1				2			3					4
				6
A = A +				1 (k				(3)	+ 2k			(3)	+ 2k		(3)		+ k		4	(3)	),
	2	1		6				1			2				3				4
				6
Вхідні дані:
B		= 50o , L = 24o , A = 45o , s = 60000 м.
1				1					1
				Позначен									Числові значення
				ня
				k11									0.00665714
				k21									0.01032792
				k31									0.00791165
				k12									0.00663054
				k22									0.01040993
				k32									0.00799670
				k13									0.00663025
				k23									0.01041021
				k33									0.00799682
				k14									0.00660326
				k24									0.01049310
				k34									0.00808272
				B2									50o22’47.60412”
				L2									24o35’47.26145”
				A2									225o27’29.480”

Розв’язування головних геодезичних задач в просторі за формулами перетворення координат

При опрацюванні просторових геодезичних мереж (без проектування їх на поверхню еліпсоїда) може виникнути потреба в розв’язуванні головної геодезичної задачі між точками в просторі, особливо часто такі задачі розв’язуються при застосуванні супутникових методів визначення координат пунктів.

3. Розв’язування головних геодезичних задач в просторі

3.1 Пряма геодезична задача.

Для розв’язування головних геодезичних задач в просторі використовують системи просторових декартових X, Y, Z, геодезичних B, L, H та топоцентричних горизонтальних (декартових x`, y`, z` та полярних A, z, D) координат і зв’язки між ними.

Постановка задачі: задані геодезичні координати B1, L1, H1 початкової

точки та топоцентричні полярні координати A1,2, z1,2, D на точку визначень, необхідно визначити її геодезичні координати B2, L2, H2.

Пряму геодезичну задачу у даному випадку розв’язують в такій послідовності:

1) Обчислення просторових декартових координат X1, Y1, Z1 початкової

точки за формулами

= (N1 + H1 ) cos B1 cos L1 ,

= (N1 + H1 ) cos B1 sin L1 ,

= (N

(1 - e2 ) + H

)sin B ,

(3.1)

- e2 sin

2 B

2) Обчислення елементів матриці перетворення Р1 координат за формулою

- sin B1 cos L1

- sin L1

cos B1 cos L1

P1 =

- sin B1 sin L1

cos L1

cos B1 sin L1

(3.2)

cos B1

sin B1

3) Обчислення топоцентричних декартових координат x2`, y2`, z2` за

формулами

x`2 = D sin z1,2 cos A1,2 ,

y`2 = D sin z1,2 sin A1,2 ,

(3.3)

z`2 = D cos z1,2 .

4) Обчислення просторових декартових координат X2, Y2, Z2 точки визначень за формулами

X 2		X1		x`2
Y2	=	Y1	+ P1	y`2	.	(3.4)
Z2		Z1		z`2

5) Обчислення геодезичних координат B2, L2, H2 за формулами

tgL

2 ,

tgBi+1

btgBi

, i = 1,2...,n,

X 2

c + tg 2 B2i

R =

ae2

c =

X 2

+ Y2 ,

- e2

R 1 - e2

H 2

- (1 - e2 )N2 .

sin B2

3.2. Обернена геодезична задача.

Постановка задачі:: задані геодезичні координати B, L, H двох

необхідно знайти топоцентричні полярні координати A1,2, z1,2, D

точки відносно першої. Задачу розв’язують у наступній послідовності:

(3.5)

точок, другої

1)За формулами (3.1) від геодезичних координат B, L, H двох точок переходять до їх просторових декартових координат X, Y, Z.

2)Обчислюють елементи транспонованої матриці перетворень координат Р2 за формулою

	- sin B2 cos L2	- sin B2 sin L2	cos B2
	- sin B2 cos L2	- sin B2 sin L2	cos B2
P2 =	- sin L2	cos L2	0	.	(3.6)
	cos B2 cos L2	cos B2 sin L2	sin B2

3) Обчислюють топоцентричні декартові координати x`, y`, z` першої точки відносно другої і навпаки за формулою

x`		X 2	- X1
x`		X 2	- X1
y`	= P2	Y2	-Y1	.	(3.7)
z`		Z2	- Z1

4) Обчислення топоцентричних полярних координат A, z, D першої точки відносно другої і навпаки за формулами

y`		x`2 + y`2		2	2	2
tgA = x`	, tgz =	z`	, D =	x`	+ y`	+z` .	(3.8)

Приклад розв’язування прямої геодезичної задачі.

1. Вхідні дані: а =6378245,0 м, е2 = 0,006693421623,

В1 = 49°50'11,4596", L1 = 24°00'17,1502", H1 = 385,471 м, А1,2 = 191°49'06,17", D = 22488,17 м, Z1,2 = 89°18'16,2". 2. Схема обчислень.

Елементи	Числові	Елементи	Числові
формул	значення	формул	значення
X1	3765581,097	B21	49°26'55,23035"
Y1	1676919,895	B22	49°38'21,75402"
Z1	4851460,864	B23	49°38'19,07969"
N1	6390748,087	B24	49°38'19,09012"
x`2	-22009,837	B25	49°38'19,09011"
y`2	-4605,464	B2	49°38'19,0901"
Z`2	272,972	L2	23°56'27,6445"
X2	3782980,826	H2	698,106 м
Y2	1679626,992
Z2	4837473,770

Приклад розв’язування оберненої геодезичної задачі.

1. Вхідні дані:

В1 = 49°50'11,4596", L1 = 24°00'17,1502", H1 = 385,471 м, В2 = 49°38'19,0901", L1 = 23°56'27,6445", H1 = 698,106 м. 2. Схема обчислень.

Елементи	Числові	Елементи	Числові
формул	значення	формул	значення
N1	6390748,087	x`2	-22009,837
X1	3765581,097	y`2	-4605,464
Y1	1676919,895	z`2	272,972
Z1	4851460,864	D	22488,17
N2	6390674,943	z1,2	89°18'16,2"
X2	3782980,826	z2,1	90°53'51,4"
Y2	1679626,992	А1,2	191°49'06,17"
Z2	4837473,770	А2,1	11°46'11,04"
x`1	22012,660
y`1	4586,550
Z`1	-352,296

Редукування елементів геодезичної мережі з еліпсоїда на площину (в проекції Гаусса-Крюгера)

Загальні відомості

Для інженерно-геодезичних робіт не є доцільним застосування системи геодезичних координат, не зважаючи на те, що вона є єдиною для всієї поверхні земного еліпсоїда, поскільки її координати отримуються шляхом досить складних обчислень і до того в дуговій мірі, а лінійні значення дугових одиниць змінюються зі зміною широти місця.

Найбільш простою є прямокутна система координат на площині, яка, однак, з поверхнею земного еліпсоїда безпосередньо не зв’язана. Як відомо, тільки досить незначні ділянки земної поверхні можна приймати за площину, а для більших територій застосування плоских прямокутних координат можливе лише через проектування частин поверхні земного еліпсоїда на площину. Тому вибір проекції для перенесення геодезичних побудов з еліпсоїда на площину становить теоретично і практично важливу задачу для геодезії. Проекції земного еліпсоїда на площині, що приймаються для перенесення і опрацювання результатів геодезичних вимірювань, називаються геодезичними проекціями.

Геодезичні проекції дають методи точного перенесення елементів поверхні еліпсоїда (ліній, кутів) на площину, тобто між поверхнею еліпсоїда та площиною встановлюється такого роду відповідність, коли кожній точці поверхні еліпсоїда відповідає одна і тільки одна точка площини, причому при неперервному русі точки по поверхні еліпсоїда відповідна їй точка на площині переміщується теж неперервно.

Загальні формули цього роду відповідності між поверхнею еліпсоїда та площиною або загальні формули геодезичних проекцій можуть бути написані в наступному виді

x = f1 (B, L),

y = f2 (B, L),

(1)

де B і L - геодезичні координати, широта і довгота, що визначають положення точки на поверхні еліпсоїда, x та y - декартові (прямокутні) координати точки на площині, а f1 і f2 - довільні функції, неперервні в області l ( l = L - Lo - довгота, яка відрахована від деякого меридіана ( Lo ), прийнятого за початковий).

В теорії геодезичних проекцій основним є встановлення взаємнооднозначної точкової відповідності між поверхнями земного еліпсоїда і площини таким чином, щоб відповідні кути геометричних фігур еліпсоїда і площини були рівними, а сторони пропорційними. Вказана відповідність визначається законом перетворення заданих геодезичних координат B,L в координати x,y на площині, чи навпаки. Загальні рівняння точкової відповідності можуть бути виражені функціональними залежностями (1).

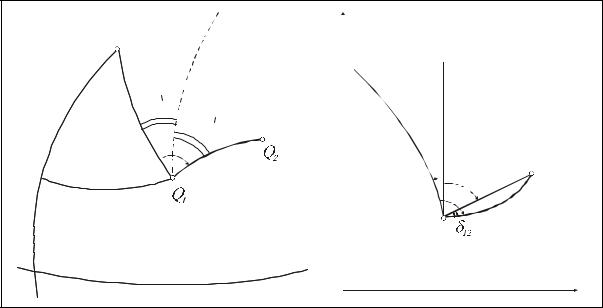
Нехай Q1 P - меридіан, що проходить через т. Q1 (рис.1 а)); Q1T - дотична до еліпсоїда і паралельна площині осьового меридіана. Кут g¢ між напрямом

меридіана	Q1 P			і дотичною	Q1T називається геодезичним зближенням
меридіанів в т. Q1 . Кут в т.					Q1 між напрямом меридіана Q1 P і геодезичною
лінією Q1Q2 є геодезичний					азимут А12 цієї лінії; кут в т. Q1 між напрямом
дотичної Q1T і напрямом					геодезичної лінії Q1Q2 є геодезичний
дирекційний				кут a12. Для поверхні еліпсоїда має місце очевидна рівність
¢	+ g	¢	.
А12 = a12

На рис. 1 б) : точки q1 і q2 - зображення точок Q1 і Q2 поверхні еліпсоїда; ор - вісь абсцис, зображення осьового меридіана ОР; q1n - зображення меридіана Q1P; крива q1q2 - зображення геодезичної лінії Q1Q2, d - хорда, що стягує цю криву між точками q1 і q2. Кут g між координатною лінією y = const і зображенням меридіана q1n називається зближенням меридіанів на площині; відраховується він від лінії y = const, тобто лінії, паралельної осі абсцис, в напрямі проти ходу годинникової стрілки. Напрямний кут a12, відрахований від координатної лінії у = const за годинниковою стрілкою до заданого напряму - до хорди q1q2 - називається дирекційним кутом на площині.

y=const

BQ1=const

ек

ватор

Рис. 1

Кут d12 між дотичною до кривої q1q2 в т. q1 і хордою d називається

поправкою за кривину зображення геодезичної лінії на площині

або редукцією напряму;

відраховується він від дотичної до кривої за ходом

годинникової стрілки до хорди. На площині має місце рівність:

α12 = А12 - γ1 - δ12 .

(2)

Границя відношення довжини відрізка S на площині до довжини відповідного йому відрізка s на еліпсоїді, коли довжина останнього стрімко наближається до нуля, називається масштабом зображення та позначається символом m .

Для визначення довжини кривої S (зображення геодезичної лінії на площині) необхідно знайти інтеграл

Q2	(3)
S = ò mds.	(3)
Q1
Якщо позначити різницю довжин кривої S та її хорди d через
δS = S - d ,	(4)
то довжина хорди d буде визначатися із рівняння
d = S - δS ,	(5)
де S обчислюється за формулою (3). З похибкою на величину 3× 10-9	можна
прийняти, що d = S.

Поправки d 12 і dS залежать від довжини кривої S та її кривини і є поправками за кривину зображення геодезичної лінії, причому перша з них вводиться в напрям лінії S, а друга - в її довжину. В загальному випадку ці залежності складні, але для редукційних задач геодезії, що виникають при переході з еліпсоїда на площину, можна вивести наближені формули, які цілком задовільняють практичні вимоги.

В проекції Гаусса осьовий меридіан зображується прямою лінією, що приймається за вісь x з масштабом m=1, тобто для точок осьового меридіана

абсциси рівні дугам меридіана від екватора, а ординати - нулю. Якщо позначити дуги меридіана від екватора до точки заданої широти через X, то для точок осьового меридіана при l=0 отримаємо:

x = X ü		(6)
y = 0	ý.
	þ

Крім того, додатнім значенням l повинні відповідати додатні значення y і від’ємним l - від’ємні y; додатнім і від’ємним l відповідають тільки додатні значення x (для північної півкулі Землі).

Областю зображення або областю розповсюдження системи плоских прямокутних координат є координатна зона, обмежена двома меридіанами, з різницею довгот в 2l 0 , переважно в 6о - шестиградусна зона. Номерація зон, а відповідно і довгота осьового меридіана, пов’язана з прийнятою номенклатурою карт. Кожна шестиградусна зона відповідає одній колоні листів

карти масштабу 1:1 000 000 і, якщо N є номером колони, то номер шестиградусної зони n визначається за формулою n = N - 30 .

Осьовий меридіан шестиградусної зони проекції Гаусса-Крюгера збігається із середнім меридіаном відповідної колони карти масштабу 1:1 000 000. Звідси виходить, що довгота осьового меридіана може бути знайдена за формулою Lo = 6n - 3o . Довгота межового меридіана шестиградусної зони відносно осьового рівна l = ±3o .

В топографічних роботах крупного масштабу застосовуються триградусні зони, а в спеціальних роботах можуть і ще вужчі, але при цьому координати опорних пунктів даються і в шестиградусній зоні.

Прямолінійне зображення осьового меридіана і екватора, які приймаються за осі декартових координат, дозволяють створити в кожній координатній зоні самостійну систему плоских координат, яка використовується у всіх видах геодезичних і топографічних робіт, що виконуються в межах однієї зони.

Системи координат в кожній зоні проекції Гаусса-Крюгера абсолютно ідентичні: плоскі координати x і y, обчислені за геодезичними координатами B, l в будь-якій координатній зоні, мають одні і ті ж значення.

Основні формули проекції Гаусса-Крюгера

При малій величині різниці довгот l = L - L0 залежність між плоскими

прямокутними координатами і геодезичними координатами для симетричних проекцій, якою є проекція Гаусса-Крюгера можна представити у вигляді наступних степеневих рядів:

X + a2l

+ a4l

+ ...

ïx

= b1l + b3l

+ b5l

...

îy

b1 = N cos B,

a2 =

N cos Bsin B,

N cos3 B(1 - tg 2 B + e'2 cos2 B),

N cos3 Bsin B(5 - tg 2 B + 9e'2 cos2 B),

N cos5 B(5 - 18tg 2 B + tg 4 B) .

120

(7)

(8)

Довжину дуги меридіана X від екватора до даної точки з широтою B можна обчислити за формулою:

X = A0 B - A2 sin 2B + A4 sin 4B - A6 sin 6B + ...

(9)

де коефіцієнти A0,A2,A4,A6, що визначаються через параметри прийнятого еліпсоїда, для еліпсоїда Красовського мають наступні значення:

A0	= 6367558.4883,
A2	=	16036.4734,
A4	=	16.8263,
A6	=	0.0216.

Формули для обчислення геодезичних координат за плоскими прямокутними координатами представляють у вигляді рядів за степенями ординати y , вважаючи її малою величиною:

B = Bx +

y2 +

y4 + ...,

(10)

l =

y +

+ ....

Широту Bx можна знайти як функцію довжини дуги меридіана на основі формули:

Bx =

x +

sin(2

x) +

sin(4

x) +

sin(6

x),

(11)

де коефіцієнти A0 , A2 , A4 , A6 для еліпсоїда Красовського будуть мати наступні значення:

A0 =1.5704606433×10-7 ,

A2 = 2.5184637×10-3 ,

A4 = 3.7002 ×10-6 ,

A6 = 7.4 ×10-9 ,

Коефіцієнти рядів () будуть визначатись за наступними формулами:


					1
b1 =					1				,
b1 =				N x cos Bx					,
		2	= -		1	tgBx		(1 + e'2 cos2		Bx ),
	a				1	tgBx
	a
					2 Nx		2

= -

(1 + 2tg 2 Bx

+ e'2 cos2 Bx ),

(12)

6 N x

3 cos Bx

tgBx

(5 + 3tg 2 Bx + 6e'2 cos2 Bx - 6tg 2 Bxe'2 cos2 Bx ),

24 Nx

(5 + 28tg 2 Bx + 24tg 4 Bx ),

120 Nx

5 cos Bx

Зближення меридіанів

2a2l + 4a4l3

tgγ =

(13)

b + 3b l 2

+ 5b l 4

В тріангуляції 2-го класу для обчислення поправок за кривину

зображення геодезичних ліній застосовують більш формули

(2y + y

);

6Rm2

(14)

= -

(2y

+ y ),

6Rm2

де Rm - середній радіус кривини, обчислений за широтою середньої точки

заданої геодезичної лінії.

Поправки за редукцію d алгебраїчно віднімаються від виміряних напрямів. Значення редукованих плоских кутів A’,B’ і C’ за виміряними на фізичній

поверхні і приведеними на еліпсоїд кутами A,B і C трикутника ABC отримують наступним чином

A'= A - (d AC - d AB ) = A - d A;
B'= B - (d BA - d BC ) = B - d B ;	(15)
C' = C - (dCB - dCA ) = C - dC .

Сума поправок за редукцію кутів трикутника рівна його сферичному надлишку з оберненим знаком, що служить контролем обчислення e та d . Справді,

A'+B'+C'= A + B + C - (d A + d B + dC ),
A + B + C = A'+B'+C'+e ,									(16)
(d A + d B + dC ) = -e.
Редуковану сторону обчислюють за формулою:
é	2		(Dy)	2	4			ù
d = sê1 +	ym	+	(Dy)		+	ym		ú.	(17)
d = sê1 +	2	+		2	+		4	ú.	(17)
ê	2			2		24Rm	4	ú
ë	2Rm		24Rm			24Rm		û

Послідовність редукування

Викладені положення дозволяють встановити наступний порядок дій при опрацюванні геодезичної мережі 2 класу в проекції Гаусса-Крюгера, якщо вихідними даними є геодезичні координати B і L одного або обох пунктів вихідної сторони, її довжина s та азимут A і горизонтальні напрями на інші сторони мережі:

·виміряні напрями приводять до поверхні еліпсоїда шляхом їх редукування з фізичної поверхні Землі;

·від геодезичних координат ( B, L ) початкового пункта (пунктів) початкової (вихідної) сторони переходять до плоских прямокутних координат ( x, y ) цього пункта (пунктів), обчисливши також при цьому значення зближення меридіанів ( γ );

·знаючи геодезичний азимут ( A ) вихідної сторони (геодезичної лінії) та зближення меридіанів ( γ ) в початковому пункті, обчислюють наближено (без

врахування поправки за кривину зображення геодезичної лінії d ) дирекційний кут зображення геодезичної лінії на площині

α'	= A	- γ .	(18)
12	12	1

Коли дані про геодезичний азимут відсутні, тоді, при відомих геодезичних координатах другого пункту початкової сторони, шляхом розв’язування оберненої геодезичної задачі на еліпсоїді, знаходять його значення або переходять від геодезичних координат цього пункта до його плоских прямокутних координат, а значення дирекційного кута на площині в цьому випадку знаходять за відомою формулою

tgα =	y2	- y1	.	(19)

12	x2	- x1

·проводять попереднє (наближене) розв’язування трикутників (для тріангуляційної мережі) та обчислення сферичних надлишків трикутників;

·за відомими координатами x та y початкового пункту, наближеним

значенням дирекційного кута α'	вихідної сторони, наближеними
12

значеннями довжин сторін мережі розв’язують послідовно прямі геодезичні задачі на площині, в результаті чого знаходять наближені координати x та y

всіх пунктів мережі. Для геодезичних мереж нижчих класів (3 і 4) наближені координати можуть бути знайдені графічно з топографічної карти;

·за наближеними координатами обчислюють довжину хорди d вихідної сторони та поправки δ за кривину зображення геодезичних ліній всіх напрямів. Сума (поправок δ в кути) і (сферичний надлишок e в кожному трикутнику) повинна дорівнювати нулю;

·поправки d вводять у виміряні напрями і отримують приведені на площину напрями хорд, після чого обчислюють приведені плоскі кути;

·проводять врівноваження мережі і отримують врівноважені значення кутів;

·за врівноваженими кутами та довжиною вихідної сторони (хорди) проводять остаточне обчислення довжин всіх сторін мережі;

·знаходять точне значення дирекційного кута вихідної сторони

α12 = A12 - γ1 - δ12

(20)

і дирекційні кути всіх сторін мережі за формулою:

α	= α	n	+ β	лів	m180o ;	(21)
n+1		n		лів

·за координатами початкового пункта, довжинами d і дирекційними кутами

αвсіх сторін обчислюють остаточні плоскі прямокутні координати x та y

всіх пунктів мережі.

ЧИСЛОВИЙ ПРИКЛАД ОПРАЦЮВАННЯ ФРАГМЕНТУ ГЕОДЕЗИЧНОЇ МЕРЕЖІ НА ПЛОЩИНІ В ПРОЕКЦІЇ ГАУССАКРЮГЕРА

Нехай фрагмент геодезичної мережі (тріангуляції) 2-го класу складається з двох трикутників (рис.2), сторона одного з них AB є вихідною стороною даної мережі, тобто відомо її довжина і геодезичний азимут; відомо також геодезичні координати вихідного пункта A :

B	B1	=51о	58’08.3168”
D	L1	=21о	50’11.3692”
	A12=177о 15’41.494”
	S12 =24796.232 м

Рис. 2

Виміряні горизонтальні кути на пунктах даної мережі (рис.2), приведені на поверхню еліпсоїда Красовського, наведені в табл. 1.

Таблиця 1

Назва	Виміряні та
Назва	приведені до
вершин	приведені до
вершин	еліпсоїда кути
	еліпсоїда кути
С	55о54’45.56”
B	55 46	30.66
A	68 18	46.67
D	60o 52’14.52”
C	56 19	23.45
B	62 48	23.90

Всі обчислення для триградусної зони виконують в послідовності наступним чином:

1)Обчислення плоских прямокутних координат пункта A за його геодезичними координатами; виконується за формулами (7). Перед обчисленнями координат встановлюють номер триградусної зони, в якій розташований пункт A , та довготу осьового меридіана L0 :

n = 7;	L = 21o ,
	0

а потім обчислюють самі координати та зближення меридіанів:

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете Вища геодезія

#
28.06.2022372.82 Кб1mtg_theme 6.pdf
#
28.06.2022240.33 Кб1mtg_theme 7.pdf
#
28.06.2022164.8 Кб1mtg_theme 8.pdf
#
28.06.2022206.31 Кб3mtg_theme 9.pdf
#
28.06.202223.3 Mб9Закатов Вища геодезія 1.pdf
#
28.06.20221.51 Mб5Лаби методичка.pdf
#
28.06.20222.93 Mб7лекції.pdf
#
28.06.20229.28 Mб15Савчук підручник.pdf
#
28.06.2022110.46 Кб6Тестові питання ОВГ_1-1.pdf
#
28.06.202289.77 Кб4Тестові питання ОВГ_2.pdf
#
28.06.2022158.89 Кб3Тестові питання ОВГ_3-2.pdf