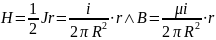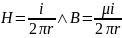- •1. Electrostatic field. Coulomb’s law. Gauss law (Электростатическое поле. Закон Кулона. Закон Гаусса)
- •Variables and units
- •Coulomb’s Law. (ЗаконКулона)
- •Electric Field Strength e and Displacement Field d. (Напряжённостьисмещениеэлектрическогополя)
- •Gauss’ Law. (ЗаконГаусса)
- •2. Poisson’s and Laplace’s equations for the potential of electric field (Уравнения Пуассона и Лапласа для потенциала электрического поля) Electric Potential. (Электрический потенциал)
- •Poisson’s and Laplace’ s equations. (Уравнения Пуассона и Лапласа)
- •3. Electrostatic Energy (Электростатическая энергия) Electrostatic Energy (Электростатическаяэнергия)
- •Virtual experiment. (Эксперимент по нахождению энергии системы)
- •Consequences (Следствия)
- •4. Power and Joule’s Law (Энергия и закон Джоуля-Ленца)
- •5. Continuity Equation (Уравнения непрерывности) ContinuityEquation (Уравнение непрерывности)
- •Image method for the flat boundary between magnetic media (Метод изображений для плоской границы между магнитными носителями)
- •8. Static magnetic field. Biot–Savart’s Law. Ampere’s Law (Статическое магнитное поле. Закон Био–Савара. Закон Ампера)
- •Variables and units (Переменные и единицы измерения)
- •Main Relations (Основные соотношения)
- •Magnetic flux density (Индукция магнитного поля)
- •Biot-Savart’s law (Закон Био-Савара)
- •Ampere’s law (Закон полного тока)
- •The cut in the space (Разрез в пространстве)
- •Laplace equation for the scalar magnetic potential (Уравнение Лапласа для скалярного магнитного потенциала)
- •10. Vector magnetic potential. Inductance (Векторный магнитный потенциал. Индуктивность)
- •Vector magnetic potential (Векторный магнитный потенциал)
- •Magnetic flux (Магнитный поток)
- •Differential equation for the vector magnetic potential (Дифференциальное уравнение для векторного магнитного потенциала)
- •Gauging of the vector magnetic potential (Калибровка векторного магнитного потенциала)
- •Integral presentation of the vector magnetic potential (Интегральное представление векторного потенциала)
- •Inductance (Индуктивность)
- •Mutual inductance (Взаимная индуктивность)
- •Inductance of thin contours (Индуктивность тонких контуров)
- •12. Internal inductance of a thin conductor (Внутренняя индуктивность тонкого проводника) Flux linkage of a thin current layer (Потокосцепление тонкого слоя с током)
- •Internal inductance of a thin conductor (Внутренняя индуктивность тонкого проводника)
- •13. Inductance of a two wire transmission line (Индуктивность двухпроводной линии).
- •14. Variable separation method in a cylindrical coordinate system (Метод разделения переменных в цилиндрической системе координат). Application of Laplace’s equation (Применение уравнения Лапласа).
- •Angular function (Угловая функция)
- •Radial function (Радиальная функция)
- •General solution of the Laplace’s equation in a cylindrical coordinate system (Общее решение уравнения Лапласа в цилиндрической системе координат)
- •15. The Faraday’s law (Закон электромагнитной индукции).
- •Lenz’s Law (правило Ленца)
- •Induction by a temporal change of b (Индукция за счёт временного изменения b)
- •16. Induction through the motion of a conductor (Индукция за счет движения проводника).
- •17. Induction by simultaneous temporal change of b and motion of the conductor (Индукция одновременным изменением b во времени и движением проводника).
- •18. Unipolar generator (Униполярный генератор).
- •19. Hering’s paradox (Парадокс Геринга)
- •20. Diffusion of magnetic fields into conductors (Распространение электромагнитного поля в проводнике)
- •21. Periodic electromagnetic fields in conductors. (Периодическое электромагнитное поле в проводниках)
- •Penetration of the electromagnetic field into a conductor. (Проникновение электромагнитного поля в проводник)
- •The skin effect. (Скин-эффект)
- •22. Poynting theorem. (Теорема Пойнтинга) Electromagnetic Field Energy. (Энергия электромагнитного поля)
- •The rate of decrease of the electromagnetic field energy in a closed volume. (Скорость уменьшения энергии электромагнитного поля в замкнутом объёме)
- •Transmission of energy in a dc line (Передача энергии в линиях постоянного тока)
- •The field picture near the wires with current (Картина поля вблизи провода с током)
- •25. Energy flows in static electric and magnetic fields (Поток энергии в статических электрических и магнитных полях).
- •26. The reduced magnetic potential (Редуцированный магнитный потенциал). Reduced scalar magnetic potential (Редуцированный скалярный магнитный потенциал)
- •Combination of scalar magnetic potential and reduced magnetic potential (Комбинация скалярного магнитного потенциала и редуцированного магнитного потенциала)
- •27. Classification of numerical methods of the electromagnetic field modeling (Классификация численных методов моделирования электромагнитного поля).
- •Classification of the problems (Классификация проблем)
- •Classification of the methods (Классификация методов)
- •28. Method of moments
- •Discretization of the problem domain (Дискретизация проблемной области)
- •29. Basic principles of the finite element method.
- •30. Finite functions (Ограниченная функция – отлична от нуля только в пределах треугольника)
- •Simplex coordinates
- •Approximation of functions inside triangles (Аппроксимация функций внутри треугольника)
- •Approximation of the equation (Аппроксимация уравнения)
- •31. Weighted residual method (метод взвешенных невязок)
- •32. Weak formulation of the electromagnetic field modeling problem
- •33. Boundary conditions in electric and magnetic fields
- •1) First type boundary conditions
- •34. Main equations of electromagnetic field in integral form.
- •35. Main equations of electromagnetic field in differential form.
- •36. Electric field of a point charge (Электрическое поле точечного заряда)
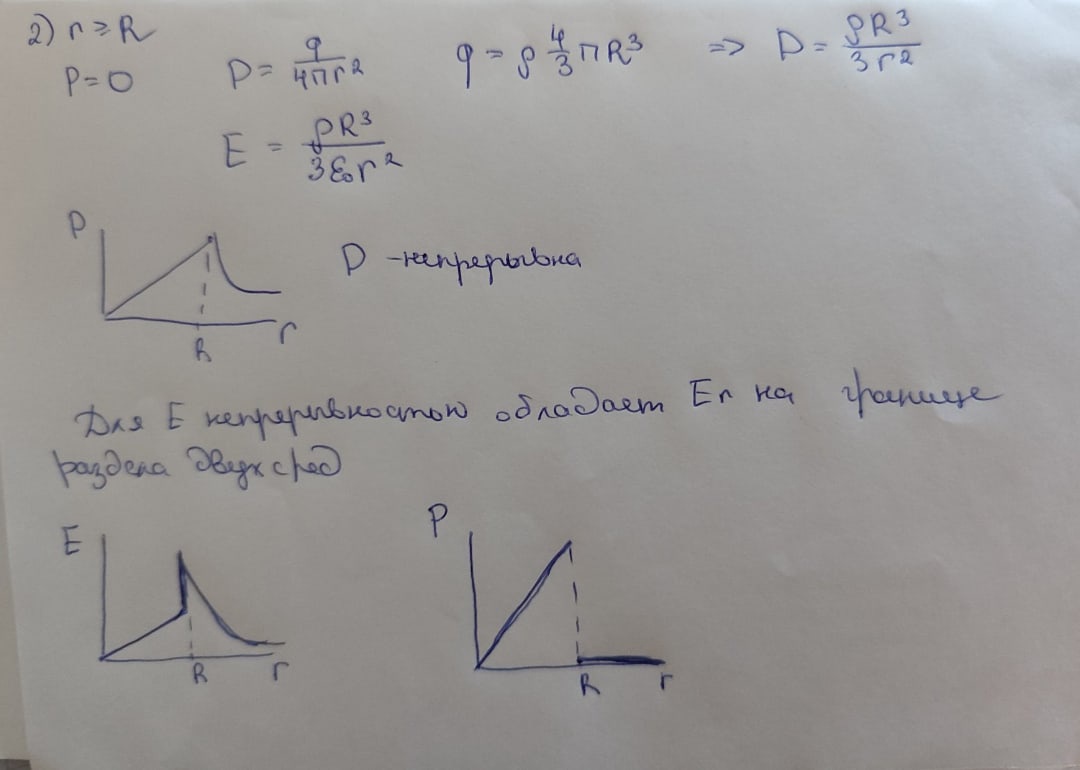
- •37. Electric field of a uniformly charged sphere (Электрическое поле равномерно заряженной сферы)
- •38. Flat capacitor. Field. Surface charge. Capacity. (Плоский конденсатор. Поле. Поверхностный заряд. Вместимость.)
- •39.2 Inductance of a cylindrical coil with the rectangular cross section(Индуктивность цилиндрической катушки прямоугольного сечения).
- •4 0.1 Electric field induced by charged line placed above conducting surface (Электрическое поле, создаваемое заряженной линией, помещенной над проводящей поверхностью).
- •4 0.2. Magnetic field induced by the line with a current placed above a ferromagnetic surface with infinitely high magnetic permeability
36. Electric field of a point charge (Электрическое поле точечного заряда)

37. Electric field of a uniformly charged sphere (Электрическое поле равномерно заряженной сферы)

38. Flat capacitor. Field. Surface charge. Capacity. (Плоский конденсатор. Поле. Поверхностный заряд. Вместимость.)
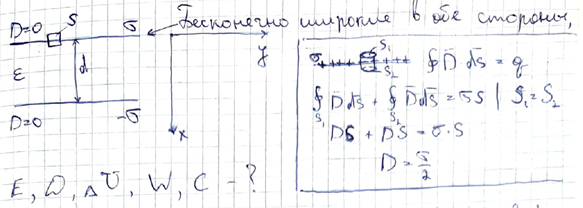
Assuming the plates are large enough so that the E field between them is uniform and directed perpendicular, then applying Gauss’s Law over surface S we find:
![]() ,
,
where S is the area of surface perpendicular to the E field and σ is the surface charge density on the plate, Therefore,
![]() Everywhere between the plates
Everywhere between the plates
![]()
Potential difference between the plates can be found from:
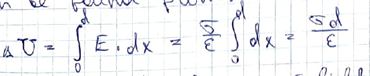
We integrate along an E field line, d is the plate separation.
The capacity can be defined as:
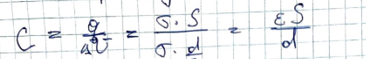
Energy can be found as:
![]()
W’ volume energy density – объемная плотность энергии
V volume between plates – объем между обкладками
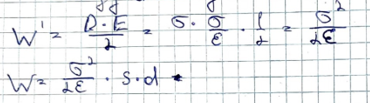
39.1 Mutual inductance between a cylindrical coil with rectangular cross section and a wire passing along the axis of the coil (Взаимная индуктивность между цилиндрической катушкой прямоугольного поперечного сечения и проводом, проходящим вдоль оси катушки)
L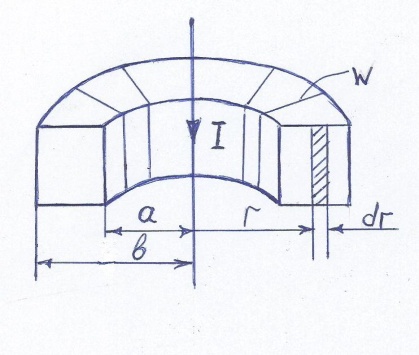 et’s
define flux of the magnetic flux density B into the fields of a
conductor through the surface S bounded by one coil winding. We know
that the B lines in this case have the shape of concentric circles
and pass the surface of each winding along the normal to it. B
depends only on the distance r. Let’s divide the surface of the
coil into small elements, within each of which the B does not change.
These are narrow strips, parallel to the conductor, with an area dS =
h ∙ dr. The desired flux Ф21
is getting by integrating over a surface S bounded by a contour:
et’s
define flux of the magnetic flux density B into the fields of a
conductor through the surface S bounded by one coil winding. We know
that the B lines in this case have the shape of concentric circles
and pass the surface of each winding along the normal to it. B
depends only on the distance r. Let’s divide the surface of the
coil into small elements, within each of which the B does not change.
These are narrow strips, parallel to the conductor, with an area dS =
h ∙ dr. The desired flux Ф21
is getting by integrating over a surface S bounded by a contour:
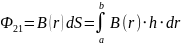
Let's find the magnetic flux density B created by an infinite conductor of radius R.
From Ampere's law, if r ≤ R then: |
From Ampere's law, if r ≥ R then |
|
|
So, magnetic flux density B created by an infinite conductor equal:
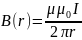
Then,
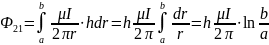
The total flux Ф21 through all windings of the coil is w times greater, so the desired mutual inductance is equal to:
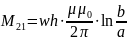
39.2 Inductance of a cylindrical coil with the rectangular cross section(Индуктивность цилиндрической катушки прямоугольного сечения).

4 0.1 Electric field induced by charged line placed above conducting surface (Электрическое поле, создаваемое заряженной линией, помещенной над проводящей поверхностью).
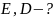
На картинке длины векторов D1 и D2 должны быть равны (обязательно) потому что у нас симметричны заряженные провода в методе изображений, одинаковые расстояния до точки от проводов, значит одинаковые модули напряжённости и электрического смещения.
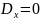 because of the symmetry. So
because of the symmetry. So
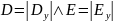 .
.
The electric displacement of a charged wire has the formula:
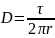
All displacement vectors are directed downwards, so the sign of the projections is negative.
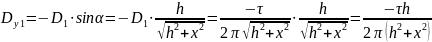
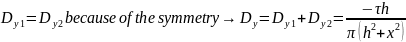
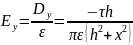
So, the modules of electric field intensity and electric displacement are simply calculated according to the following formulas:
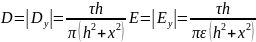
4 0.2. Magnetic field induced by the line with a current placed above a ferromagnetic surface with infinitely high magnetic permeability
In short: here the inductance of a two-wire line is calculated using the images method.
We can represent the inductance as the sum of the internal inductance (of the wire itself) and the inductance from the other wire and the images (of these wires).
The
internal inductance of one wire is
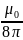 ,
but since we are looking for the inductance of the system of two
wires, so we multiply by 2. And we get
,
but since we are looking for the inductance of the system of two
wires, so we multiply by 2. And we get
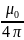 .
.
Now we consider the external inductance. The formula is as follows: the flux linkage by current. We find the flux linkage of each wire and images.
First Ф1 and Ф2. The formula for the flux is the integral of BdS. And B = µ0H, where .Substituting the value of B and finding of the integration limits (from the edge of the wire, to the middle of the other wire), we get the value for Ф1.
And Ф2 = Ф 1, because we integrate in the opposite direction, but similarly (this is one "-" sign) and then the current itself is negative; it turns out minus by minus +.
Futher, we find the images flux by integrating from the point of the first wire to the point of the second.
And we substitute everything into the formulas above