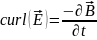- •1. Electrostatic field. Coulomb’s law. Gauss law (Электростатическое поле. Закон Кулона. Закон Гаусса)
- •Variables and units
- •Coulomb’s Law. (ЗаконКулона)
- •Electric Field Strength e and Displacement Field d. (Напряжённостьисмещениеэлектрическогополя)
- •Gauss’ Law. (ЗаконГаусса)
- •2. Poisson’s and Laplace’s equations for the potential of electric field (Уравнения Пуассона и Лапласа для потенциала электрического поля) Electric Potential. (Электрический потенциал)
- •Poisson’s and Laplace’ s equations. (Уравнения Пуассона и Лапласа)
- •3. Electrostatic Energy (Электростатическая энергия) Electrostatic Energy (Электростатическаяэнергия)
- •Virtual experiment. (Эксперимент по нахождению энергии системы)
- •Consequences (Следствия)
- •4. Power and Joule’s Law (Энергия и закон Джоуля-Ленца)
- •5. Continuity Equation (Уравнения непрерывности) ContinuityEquation (Уравнение непрерывности)
- •Image method for the flat boundary between magnetic media (Метод изображений для плоской границы между магнитными носителями)
- •8. Static magnetic field. Biot–Savart’s Law. Ampere’s Law (Статическое магнитное поле. Закон Био–Савара. Закон Ампера)
- •Variables and units (Переменные и единицы измерения)
- •Main Relations (Основные соотношения)
- •Magnetic flux density (Индукция магнитного поля)
- •Biot-Savart’s law (Закон Био-Савара)
- •Ampere’s law (Закон полного тока)
- •The cut in the space (Разрез в пространстве)
- •Laplace equation for the scalar magnetic potential (Уравнение Лапласа для скалярного магнитного потенциала)
- •10. Vector magnetic potential. Inductance (Векторный магнитный потенциал. Индуктивность)
- •Vector magnetic potential (Векторный магнитный потенциал)
- •Magnetic flux (Магнитный поток)
- •Differential equation for the vector magnetic potential (Дифференциальное уравнение для векторного магнитного потенциала)
- •Gauging of the vector magnetic potential (Калибровка векторного магнитного потенциала)
- •Integral presentation of the vector magnetic potential (Интегральное представление векторного потенциала)
- •Inductance (Индуктивность)
- •Mutual inductance (Взаимная индуктивность)
- •Inductance of thin contours (Индуктивность тонких контуров)
- •12. Internal inductance of a thin conductor (Внутренняя индуктивность тонкого проводника) Flux linkage of a thin current layer (Потокосцепление тонкого слоя с током)
- •Internal inductance of a thin conductor (Внутренняя индуктивность тонкого проводника)
- •13. Inductance of a two wire transmission line (Индуктивность двухпроводной линии).
- •14. Variable separation method in a cylindrical coordinate system (Метод разделения переменных в цилиндрической системе координат). Application of Laplace’s equation (Применение уравнения Лапласа).
- •Angular function (Угловая функция)
- •Radial function (Радиальная функция)
- •General solution of the Laplace’s equation in a cylindrical coordinate system (Общее решение уравнения Лапласа в цилиндрической системе координат)
- •15. The Faraday’s law (Закон электромагнитной индукции).
- •Lenz’s Law (правило Ленца)
- •Induction by a temporal change of b (Индукция за счёт временного изменения b)
- •16. Induction through the motion of a conductor (Индукция за счет движения проводника).
- •17. Induction by simultaneous temporal change of b and motion of the conductor (Индукция одновременным изменением b во времени и движением проводника).
- •18. Unipolar generator (Униполярный генератор).
- •19. Hering’s paradox (Парадокс Геринга)
- •20. Diffusion of magnetic fields into conductors (Распространение электромагнитного поля в проводнике)
- •21. Periodic electromagnetic fields in conductors. (Периодическое электромагнитное поле в проводниках)
- •Penetration of the electromagnetic field into a conductor. (Проникновение электромагнитного поля в проводник)
- •The skin effect. (Скин-эффект)
- •22. Poynting theorem. (Теорема Пойнтинга) Electromagnetic Field Energy. (Энергия электромагнитного поля)
- •The rate of decrease of the electromagnetic field energy in a closed volume. (Скорость уменьшения энергии электромагнитного поля в замкнутом объёме)
- •Transmission of energy in a dc line (Передача энергии в линиях постоянного тока)
- •The field picture near the wires with current (Картина поля вблизи провода с током)
- •25. Energy flows in static electric and magnetic fields (Поток энергии в статических электрических и магнитных полях).
- •26. The reduced magnetic potential (Редуцированный магнитный потенциал). Reduced scalar magnetic potential (Редуцированный скалярный магнитный потенциал)
- •Combination of scalar magnetic potential and reduced magnetic potential (Комбинация скалярного магнитного потенциала и редуцированного магнитного потенциала)
- •27. Classification of numerical methods of the electromagnetic field modeling (Классификация численных методов моделирования электромагнитного поля).
- •Classification of the problems (Классификация проблем)
- •Classification of the methods (Классификация методов)
- •28. Method of moments
- •Discretization of the problem domain (Дискретизация проблемной области)
- •29. Basic principles of the finite element method.
- •30. Finite functions (Ограниченная функция – отлична от нуля только в пределах треугольника)
- •Simplex coordinates
- •Approximation of functions inside triangles (Аппроксимация функций внутри треугольника)
- •Approximation of the equation (Аппроксимация уравнения)
- •31. Weighted residual method (метод взвешенных невязок)
- •32. Weak formulation of the electromagnetic field modeling problem
- •33. Boundary conditions in electric and magnetic fields
- •1) First type boundary conditions
- •34. Main equations of electromagnetic field in integral form.
- •35. Main equations of electromagnetic field in differential form.
- •36. Electric field of a point charge (Электрическое поле точечного заряда)
- •37. Electric field of a uniformly charged sphere (Электрическое поле равномерно заряженной сферы)
- •38. Flat capacitor. Field. Surface charge. Capacity. (Плоский конденсатор. Поле. Поверхностный заряд. Вместимость.)
- •39.2 Inductance of a cylindrical coil with the rectangular cross section(Индуктивность цилиндрической катушки прямоугольного сечения).
- •4 0.1 Electric field induced by charged line placed above conducting surface (Электрическое поле, создаваемое заряженной линией, помещенной над проводящей поверхностью).
- •4 0.2. Magnetic field induced by the line with a current placed above a ferromagnetic surface with infinitely high magnetic permeability
33. Boundary conditions in electric and magnetic fields
1) First type boundary conditions
L![]() et’s
assume we know 1-st type boundary conditions.
et’s
assume we know 1-st type boundary conditions.
W![]() hat
does that mean? We know potential distribution over the boundary, so
we simply do not need to solve this equation in the boundary nodes,
because we already know the solution, that’s why this second term,
which includes the integral over the whole boundary is not used at
all.
hat
does that mean? We know potential distribution over the boundary, so
we simply do not need to solve this equation in the boundary nodes,
because we already know the solution, that’s why this second term,
which includes the integral over the whole boundary is not used at
all.
It is not necessary for the nodes which are placed inside the problem domain, and we already know the solution for all external nodes. That’s a lucky situation and so we completely got view of this second term. In principle, sometimes when we work with the second type boundary conditions the situation is more complicated. The 1-st type boundary conditions keep a symmetry of the main problem matrix.
2) 2-nd type boundary conditions (Второй тип граничных условий)
2-nd type boundary conditions assume the normal derivative of the potential is equal to some function.
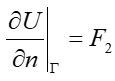
And we have here an integral along the boundary and we can substitute the boundary conditions of the second type inside this relation and we shall get a final result.
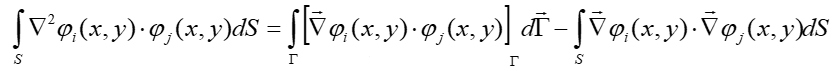
T he equation for the external nodes, which are placed at the boundary, are more complex. The exception corresponds to the case when this function F2 is equal to zero, in such a case the form of the coefficients will be identical because this derivative is equal to zero the first integral in the right part also will be equal to zero. The 2-nd type boundary conditions of the dU/dn = 0 is most often used boundary condition, so in such a case if we have such a situation than we can say the expression for the coefficients within the finite element method is always the same and it is described by these simple relations.
34. Main equations of electromagnetic field in integral form.
1) Gauss’s Law
Definition of the electric flux:
T otal electric flux passing any closed surface is equal to the total charge enclosed by that surface.
Gauss law for the field displacement Gauss law for the field intensity
2) Electric potential
The
integral
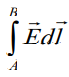 solely (только)
depends on the points A and B but not on the particular path taken
from A to B.
solely (только)
depends on the points A and B but not on the particular path taken
from A to B.
Definition of the potential:
3) Ohm’s Law
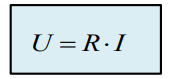
4) Joule’s law
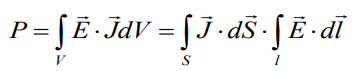
P – power
5) Gauss’s Law for for the magnetic field:
There are no magnetic charges in the nature:
6) Amphere’s Law
I – is the current crossing the surface limited by this contour
7) Faraday’s Law
The electromotive force induced in a closed contour is equal to rate of changing magnetic flux in time with opposite signs
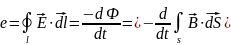
35. Main equations of electromagnetic field in differential form.
1) Gauss’s Law
Definition of the electric flux:
T otal electric flux passing any closed surface is equal to the total charge enclosed by that surface.
Gauss law for the field displacement Gauss law for the field intensity
2) Electric potential
![]()
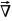 – nabla
– nabla
3) Laplace’s equation
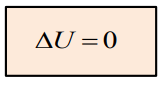
(When )
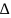 – delta (Laplace operator)
– delta (Laplace operator)
4) Poisson’s equation
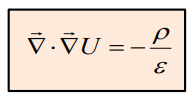 – nabla
– nabla
5) Ohm’s Law
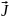 – current density
– current density
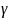 – conductivity
– conductivity
6) Joule’s law
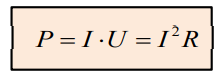
P – power
7) continuity equation
for steady currents (charge is constant):
![]() 8)
Gauss’s law for magnetism
8)
Gauss’s law for magnetism
(i.e., magnetic field has no sources)
9) Ampere’s law
10) Scalar magnetic potential
Um – magnetic potential. The unit is – A (Ampere)
11)
12) Differential equation for the vector magnetic potential
13) Faraday’s Law of induction
The curl of electric field E is equal to the negative rate of change of the magnetic field B