The skin effect. (Скин-эффект)

The maximum value of the amplitude of the electromagnetic field corresponds to the left and right side of the conducting plate. When we move into the center of the conducting plate, the magnetic field decreases, and the amplitude become smaller and smaller. In the center the disappearing is almost completes.

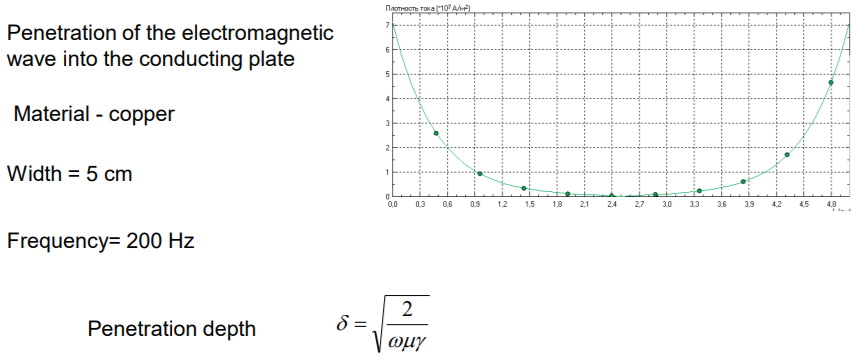
Penetration depth:

Penetration length – it’s the position where the amplitude decreases by the e = 2.73

22. Poynting theorem. (Теорема Пойнтинга) Electromagnetic Field Energy. (Энергия электромагнитного поля)

The energy of the electromagnetic field enclosed inside a certain volume V, bounded by a closed surface S, is determined by the volume energy density of the electric and magnetic fields.

To determine the rate of the energy variation in time dependent electromagnetic field, it is necessary to differentiate the corresponding expression by time:

The rate of decrease of the electromagnetic field energy in a closed volume. (Скорость уменьшения энергии электромагнитного поля в замкнутом объёме)

The main relations between the characteristics of the electromagnetic field:

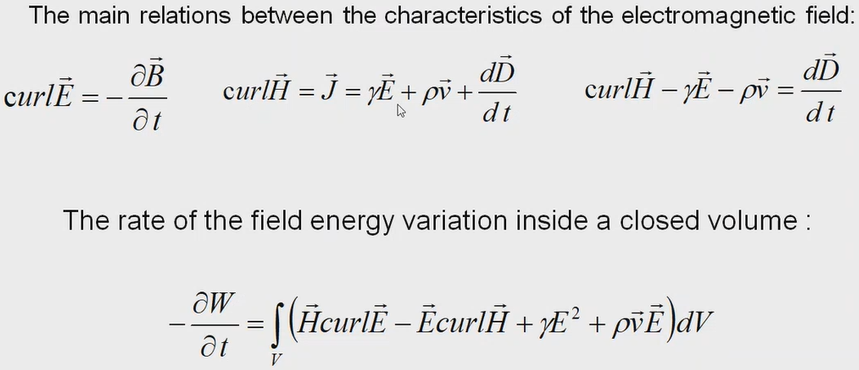
The rate of the field energy variation inside a closed volume:

T he volume of divergence of any vector may be replaced by the integral of the closed surface of this volume.

Using the algebra formula , we get:

After applying the Gauss theorem:

The resulting expression is called the Poynting’s theorem:

The first term of this expression corresponds to energy losses for heating the conductor.

The second term is equal to the energy of the electric field spent on the acceleration of charged particles in the volume V.

The third term characterizes the energy of the electromagnetic fields carries across the boundaries of the area.

The power of radiated electromagnetic energy is numerically equal to the flow of energy through the surface per unit of time.

The Poynting vector:

The energy of the electromagnetic field is transmitted if the electric and magnetic intensity vectors are nor parallel.

23. Transmission of energy in 2-wire line loaded on a resistor (передача энергии по 2-проводной линии, нагруженной резистором)

Energy flows in the electromagnetic field

(Поток энергии в электромагнитном поле)

The energy flows take place in the time dependent electromagnetic fields. We just have seen that Poynting’s theorem claims. If the electromagnetic field depends on time it may cross the surface and so the total energy that was concentrated inside the volume may decrease or may increase as well. But also, we shall see that in static field nevertheless energy flow exists. The energy transmitted along the wires of the line is propagated in the dielectric, as well as the energy emitted by the antenna. Wires and cables only serve as guide for this energy.

Now, let’s consider two wire transmission lines which is loaded and the load is a resistor.

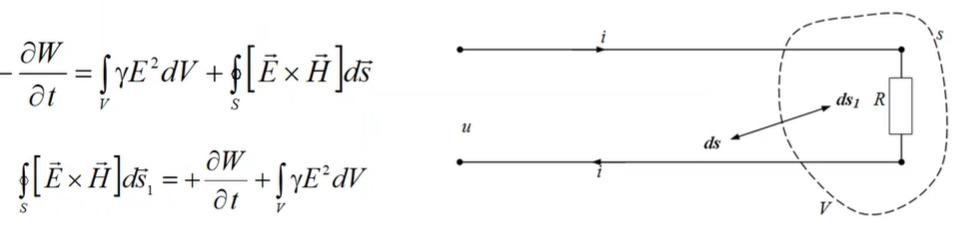
We should consider an electromagnetic field which is induced by all these wires. ∂W over ∂t (∂W/∂t). By the way in this case, in principle does not matter the time dependence of this current, it may be static current which does not depend on time but may be current that changes in time. According to the Poynting’s theorem ∂W/∂t may be expressed in this form.

What is V and S? We shall surround the space with the resistor in the load by the surface S and everything which is inside will be volume V. So, what we shall have inside the volume? The first term corresponds to the power losses inside the conducting material and that will be the resistor. Also, we should take in account that energy of the electromagnetic field may cross the surface which is described by this area S and this first term with V. We can find or we can express this integral from the Poynting vector as the sum of these two components:

So, we can conclude that increase in the electromagnetic field energy stored inside the volume and release of the thermal energy in the line wires and the load can occur only due to the influx of electromagnetic energy which enters this volume, which crosses this area S. If the current is static then the field distribution inside that volume will be constant. So ∂W/∂t will be equal to zero as well. In this case all energy which is dissipated (рассеянный) in this resistor will cross this surface and may be calculated as a vector product of E and H. The dissipated energy of this element can be very small, let’s neglect the energy, which is dissipated inside the wires, but the energy comes not through the wires, but through the space which surrounds these wires, lines here is only "subguides" (вспомогательные направляющие), guides along which the energy of the electromagnetic fields propagates (распространяется) and change their position.