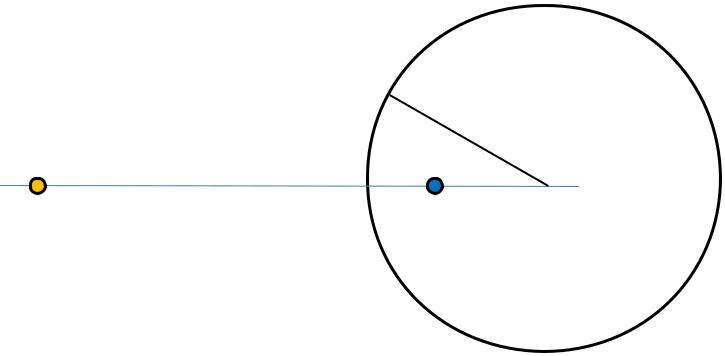
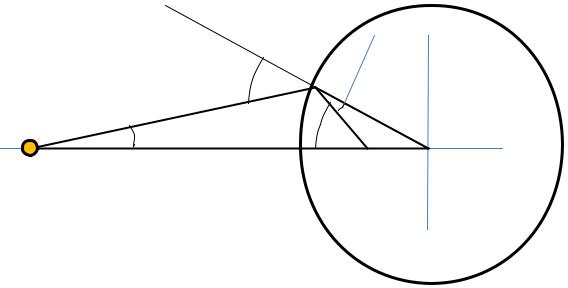
The inverse point
The inverse point is located inside a circle
r
A B C
A position of inverse point is defined by a relation
AC BC r2
11
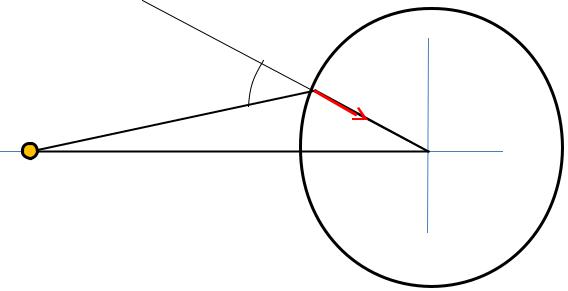
Normal component of the field intensity
The normal component of |
|
|
P |
|||
the external field intensity |
b |
En |
||||
|
||||||
|
|
cos( ) |
|
|
|
|
En(ext) |
|
|
|
|||
2 0 |
b |
A |
|
|
||
|
|
|
||||
|
|
surface charges: |
|
|
||
|
|
(x) 1 |
2 2D(ext) |
|
|
|
|
|
1 |
n |
|
|
|
|
|
2 |
|
|
||
C
2
1 0
Field displacement induced by surface charges:
|
(x) |
1 |
2 |
(ext ) |
|
|
|
|
|
Dn |
|
Dn |
2 |
2 |
|||
|
|
1 |
|
||
12
Normal component of the field intensity
Field intensity induced by |
|
|
|
the surface charges: |
A |
|
|
|
|
|
2 |
1 |
|
|
|
|
|
cos( ) |
|||||
En |
|
|
|
|
|
|
|
b |
|
|
2 |
|
|||||
|
|
2 0 |
1 |
|||||
Normal component of the field intensity outside the cylinders:
|
|
P |
|
b |
Bn |
||
|
C
(ext ) |
( ) |
En En |
|
En |
To find a proper solution of the problem outside the cylinder it is |
|
enough to ensure the right values of the normal component of the |
|
field intensity along the interface! |
13 |
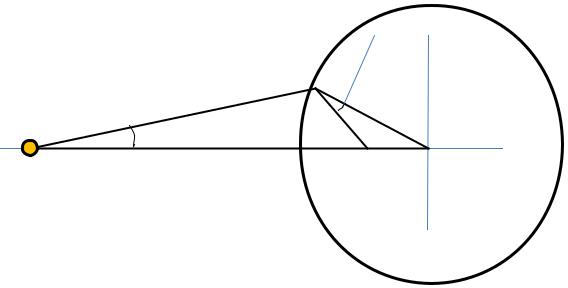
Geometrical relations
Wire with the linear charge
density of τ is located in the point A
P is an arbitrary point at the circle
B is the inverse point
|
|
P |
|
|
|
|
|
|
|
|
C |
|
|
||
A |
|
|
B |
Consider triangles APC and PCB
|
AC |
PC |
PC r |
1. |
PC |
BC |
2.Angle C is common
The triangles are similar !
14
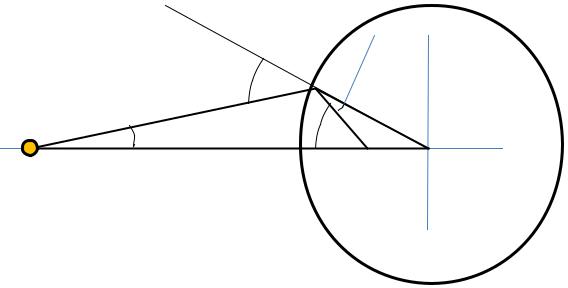
Angles
APQ 180 APB |
|
Q |
|
|
|
|
P |
|
|
|
|
|
||
ABP 180 APB |
|
|
|
|
|
|
|
C |
|
|
|
|
||
|
|
|||
|
A |
|
|
B |
APQ ABP
15
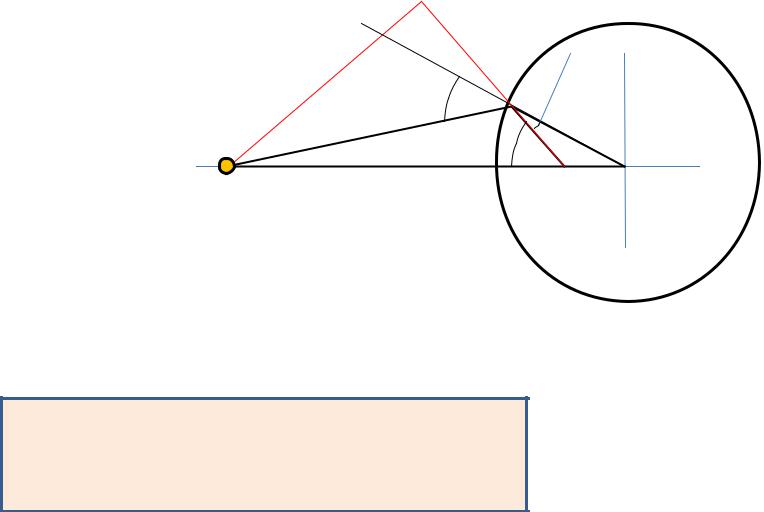
Geometrical relations
Wire with the linear charge
density of τ is located in the point A
P is an arbitrary point at the circle
B is the inverse point
b
A
Evidently |
AB b cos( ) a cos( ) |
|
From the red triangle: |
AB sin( ) AO |
|
OO 90
a
C
B
b sin( ) AO
So we get |
b cos( ) a cos( ) b sin( ) |
|
sin( ) |
16
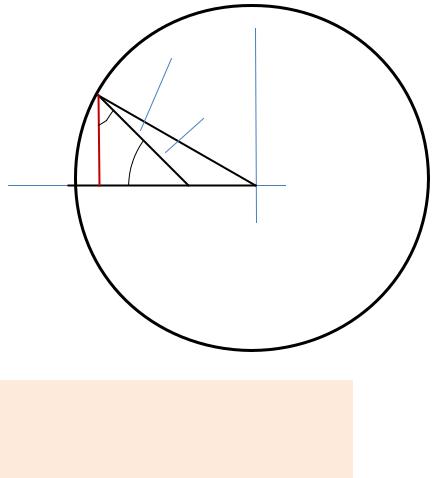
Geometrical relations
PQ a sin( )
PQ r sin( )
Inside a triangle a sum of angles is 180º:
90 180
90 180
So we have:
P
ra
C
QB
Combining all these relations: |
a sin( ) r sin( ) |
|
|
17
Trigonometric relations
We just have got two relations: |
b cos( ) a cos( ) b sin( ) |
a sin( ) r sin( ) |
|
|
sin( ) |
Let us combine them: |
|
b cos( ) a cos( ) a b sin( ) r sin( )
Taking into account: sin( ) sin( ) sin( ) sin( )
2
sin( ) ar sin( )
sin( ) sin( ) 2 sin( ) cos( ) sin( ) 2ar sin( ) cos( )
18
Trigonometric relations
b cos( ) a cos( ) a b sin( ) r sin( )
sin( ) sin( ) 2 sin( ) cos( ) sin( ) 2ar sin( ) cos( )
b cos( ) a cos( ) |
a b sin( ) |
|
r sin( ) |
a b 2r cos( ) sin( ) r a sin( )
b cos( ) a cos( ) |
a b |
b 2 cos( ) |
: ab |
|
r |
|
|
We shall get: |
cos( ) |
|
cos( ) |
1 |
|
b |
|
a |
r |
||
|
19
Geometrical relations
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
cos( ) |
|
cos( ) |
|
1 |
|
|
|
|
|||||||
|
|
|
|
a |
C |
||||||||||
|
b |
|
|
a |
|
r |
|
|
|||||||
|
|
|
|
|
|
A |
|
|
B |
|
|||||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
cos( ) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
En |
|
|
|
2 |
|
|
|
|
b |
|
|
|
|
||
|
|
2 0 |
1 |
|
|
|
|
||||||||
The normal component of the field intensity induced by the surface charges may be expressed as
|
|
|
|
2 |
1 |
|
|
|
|
|
2 |
1 |
|
1 |
|
|
|
|
cos( ) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
En |
|
|
2 |
|
|
a |
|
|
2 |
|
|
|
|||
|
|
2 0 |
1 |
|
2 0 |
1 r |
|||||||||
20