Экспериментальные методы исследований. Калинин Ю.Е

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Если р зависит от температуры как

exp H p / RT ,

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

9.39 Mб

Скачать

☆

<<< < Предыдущая 16 17 18 19 20 21 22 23 24 25 26 2728 / 5428 29 30 31 32 33 34 35 36 37 38 39 40 > Следующая >>>

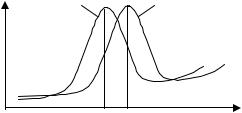
-1	1	2
Q

Т1 Т2

Рис. 5.23. Максимумы внутреннего трения, полученные на частотах 1 и 2

Для вычисления энергии активации Н по (5.45) с достаточной точностью необходимо изменять частоту на несколько порядков. Поскольку измерения проводятся на одной установке, то изменить частоту более чем на порядок бывает затруднительно. Поэтому величина T оказывается довольно малой (~ 20-30 К). Вследствие неопределенности определения температуры максимума величина ошибки при определении Н может достигать 20 и более %. Повысить точность измерения Н можно при ее определении по тангенсу угла наклона зависимости частоты от обратной температуры положения максимума в координатах ln =f(1/T) (полученных на различных частотах) или определяя T как сдвиг максимума. Этому, однако, мешают два обстоятельства. Изменение частоты приводит к расширению реального максимума на кривой Q-1. Кроме того, часто уменьшается высота максимума, что связано с зависимостью степени релаксации от температуры, а также с наличием спектра времен релаксации. Для более точного определения температуры максимума их строят за вычетом фона внутреннего трения (см. рис. 5.24).

Если имеется спектр времен релаксации, вычисление Н по выражению (5.45) дает усредненную энергию активации.

271

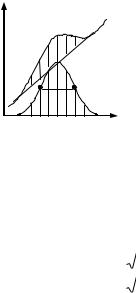
Построение максимумов внутреннего трения за вычетом фона дает возможность установить, имеется ли спектр энергий активаций или нет. Если изменение частоты не приводит к изменению формы максимума на кривой Q-1(Т), то процесс характеризуется одной энергией активации. В противном случае имеется спектр энергий Нi.

Если релаксационный процесс определяется одним временем релаксации, то полуширина максимума п 1/ T определяется по выражению

Q-1

Тл Тп Т

Рис. 5.24. Построение максимума за вычетом фона из кривой температурной зависимости Q-1

	1		R		2	3
п				ln			.	(5.47)
п				ln			.	(5.47)
T		теор	H		2	3

Сравнивая экспериментальную полуширину максимума Q-1 с теоретической, определяемой по выражению (5.47), оценивают уширение пика внутреннего трения. Экспериментальная полуширина максимума определяется по выражению

	1		1		1
п							,	(5.48)
п							,	(5.48)
T		экс	Т	л	Т	п

272

где Тл

и Тп – температуры, соответствующие точкам на полуширине максимума внутреннего трения с левой и правой стороны.

5.4.2.2. Определение энергии активации по форме максимума внутреннего трения

Этот способ определения Н заключается в использовании низкотемпературной или высокотемпературной ветви (за вычетом фона) пика Q-1(Т). Действительно, из

формул Q 1		1	и Q 1		можно записать

max	2			1 2 2

1 2Q 1

Q max . (5.49) 1 2 2

Тогда из формул (5.43) и (5.49) следует для низкотемпературной ветви пика (>>1)

Q 1		H
	~ exp		,	(5.50)

		RT
для высокотемпературной ветви пика ( <<1)
Q 1		H
	~ exp		.	(5.51)

		RT

Из формул (5.50) и (5.51) следует, что Н можно определить по углу наклона низкотемпературной или высокотемпературной ветви пика Q-1(Т) в координатах lnQ-1 – 1/Т. Этот способ определения Н следует применять только для хорошо выраженных узких пиков.

273

5.4.2.3. Определение энергии активации по полувысоте релаксационного максимума

Этот способ вычисления Н основан на определении полувысоты пика 12 Qmax1 4 . Тогда, учитывая (5.43), можно записать


			0 ехр Н / RT1/ 2			, или
4		1 2 2		ехр 2Н / RT		, или
		0		1/ 2
	1		0 ехр Н / RT1/ 2		.		(5.52)
	4	1 0 ехр Н / RT1/ 2 2			.		(5.52)

Здесь T1/ 2 - температура на половине высоты максимума со

стороны низких температур (рис. 5.25). С другой стороны, из выражения

0 ехр(Н/RTмакс) =1

имеем

0 = ехр(-Н/RTмакс).

(5.53)

Подставим (5.53) в (5.52), получим

274

ехр

Т1/ 2

Т макс

2Н

1 ехр

Т1/ 2

макс

Решим это уравнение относительно

ехр

Т1/ 2

Т макс

или у2 – 4у + 1 = 0; у1,2= 2

Имеем

3 .

1 у2

2Н

ехр

= 2

3 ,

R Т1/ 2

Тмакс

или

Н Тмакс

Т1/ 2

ln(2 ±

3) .

Т1/ 2 Тмакс

Отсюда

RТ1/ 2Т макс

1,31 .

Т макс

Т1/ 2

=у.

(5.54)

Если брать температуры Т1 и Т2 на полувысоте максимума, то выражение для определения энергии активации приобретает вид

Н	2,62RТ1Т 2	.	(5.55)

	Т 2 Т1

275

Q-1	Q	-1
	Q	макс
		Т
			Qмакс/2
Т1	Тмакс Т2		Т

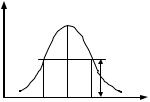
Рис. 5.25. К определению энергии активации по полувысоте максимума внутреннего трения

Вычисленная по выражениям (5.54) и (5.55) энергия активации дает правильный результат, если процесс характеризуется одним временем релаксации.

5.4.2.4.Определение энергии активации по температурному положению максимума внутреннего трения

Если имеются трудности, не позволяющие изменить частоту колебаний на 1,5-2 порядка, экспериментаторы очень часто для определения энергии активации используют способ, предложенный Марксом и Вертом в 1953 году.

Рассматривая энергию активации, связанную с диффузионными процессами в различных системах, Верт и Маркс пришли к выводу о том, что в координатах Н и Т все экспериментальные точки, полученные на одной частоте, ложатся на одну прямую. В качестве основы для получения выражения, по которому можно было определять энергию активации, использовались закономерности диффузии внедренных атомов в ОЦК решетке. Среднее время жизни внедренного атома в данном положении определяется выражением

276

1n exp S / R

exp H / RT ,

exp H / RT
n exp S / R .	(5.56)

Здесь число n – число элементарных диффузионных путей в выбранном случае. Для ОЦК решетки n = 4; - частота колебаний внедренного атома; S – энтропия активации и Н – энергия активации диффузионного процесса. Частота может различаться в разных системах, но не более чем в два раза. Обычно берется средняя величина 1,2 1013 Гц.

Среднее время жизни атомов в данном положении связано с временем релаксации р по следующему выражению:

(5.57)

4 f

где f m - частота колебаний образца. Тогда

exp H / RT n exp S / R ,

или

H / RT ln

S .

Поскольку n = 4, H RT ln / fm T / S .

4 f m

Считая, что = кТ/h, получаем окончательное выражение для определения энергии активации методом Верта-Маркса

H RT		ln	кТmax	T S ,	(5.58)
H RT	max	ln	hfmax	T S ,	(5.58)
	max

где Тmax – температура максимума Q-1.

Выражение (5.58) очень часто применяют для нахождения Н вследствие его простоты. Однако при использовании этой формулы следует иметь в виду её ограниченность некоторыми специальными видами релаксации. Применяя эту формулу, мы заранее предполагаем,

277

что предэкспоненциальный множитель 0 практически одинаков для всех релаксационных процессов и по порядку величины равен 10-13 сек. В то же время имеется ряд механизмов внутреннего трения, когда 0 на несколько порядков отличается от указанной величины (термически активированное преодоление дислокациями барьеров Пайерлса, взаимодействие дислокаций и границ доменов с подвижными точечными дефектами, диффузионное перераспределение точечных дефектов в неоднородном поле напряжений и др.). Следовательно, формулу (5.58) можно использовать лишь в случае, если процесс релаксации связан с термически активированным перемещением атомов на расстояние порядка межатомного.

5.4.3. Исследование коэффициента диффузии методом внутреннего трения

Диффузия определяется движением атомов в твердом теле, причем атомы проходят макроскопические расстояния (около 1 мкм и более). Движение атомов состоит из большого числа скачков каждого атома, преодолевающего некоторое расстояние. Для установления связи между расстоянием, пройденным диффундирующим атомом, и затраченным на это временем в основном используется уравнение Эйнштейна или какая-либо его модификация

	2 2Dt .	(5.59)
х

Здесь х 2 - средняя величина квадрата расстояния, пройденного диффундирующим атомом в данном направлении; D – коэффициент диффузии; а t – время.

Если рассматривать диффузию как задачу о беспорядочном движении, то её можно определить с помощью микроскопических данных, которые описывают скачки

278

отдельных атомов. Пусть f – частота, с которой атом движется от одного узла кристалла к другому узлу, а d – расстояние, которое он проходит при каждом скачке. Если скачки случайны по направлению, то средняя величина квадрата расстояния, на которое продвигается атом в направлении х за время t, равна

		2	fd 2		t .	(5.60)
	х		fd 2
	х		3
			3
Сравнивая (5.59) и (5.60), имеем
	D		fd 2	.		(5.61)
	D		6	.		(5.61)
			6

Выражение (5.61) применимо для ОЦК, ГЦК и простой кубической решетки.

Величина f часто заменяется в этом выражении на среднее время «оседлой жизни» атома в данном узле, определяемое как = 1/f.

Тогда
D	d 2	.	(5.62)

	6

При измерении коэффициента диффузии D химическим или радиоактивным методом не определяется. Если же для измерения D пользоваться методами внутреннего трения, то возникает возможность непосредственного определения времени .

Проявление релаксационного процесса, связанного с диффузией, выражается в том, что при определенной частоте колебаний образца на кривой Q-1(T) или Q-1(f) возникает максимум при выполнении условия р = 1. Здесь р – время релаксации. Для тех релаксационных процессов, которые

279

обусловлены движением атомов, время неупругой релаксациир и среднее время скачка считаются пропорциональными друг другу, т.е.

	= р .		(5.63)
Коэффициент пропорциональности в общем случае
определяется выражением
	N n n
		.	(5.64)
	N N n
Здесь N – число эквивалентных положений диффундирующего
атома в решетке в отсутствие напряжения ;			N - число

предпочтительных положений, возникающих в связи с приложением к образцу напряжения ; n – число эквивалентных ближайших позиций в отсутствие напряжения; n - число выгодных ближайших позиций при наличии напряжения.

Выражение (5.64) применимо только в тех случаях, когда напряжение вызывает различную заселенность двух конфигураций.

Формулу (5.62) с учетом (5.63) можно записать в виде

280

<<< < Предыдущая 16 17 18 19 20 21 22 23 24 25 26 2728 / 5428 29 30 31 32 33 34 35 36 37 38 39 40 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]