Учебники 80163

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Воронежский государственный архитектурно-строительный университет

Е.И. Ханкин

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Курс лекций

Рекомендовано в качестве учебного пособия редакционно-издательским советом Воронежского государственного архитектурно-строительного университета для студентов, обучающихся по направлениям 270200 «Транспортное строительство» и 190200 «Транспортные машины

и транспортно-технологические комплексы»

Воронеж 2009

1

Лекция 1

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

1.ЗАДАЧИ, ПРИВОДЯЩИЕ

КДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

При решении многих геометрических и физических задач приходится отыскивать неизвестную функцию по данному соотношению между этой не-

известной функцией, ее производными и независимыми переменными. Такое со-

отношение называется дифференциальным уравнением, а отыскание функции,

удовлетворяющей уравнению, называется решением или интегрированием

данного уравнения.

Рассмотрим несколько задач, приводящих к дифференциальным уравне-

ниям.

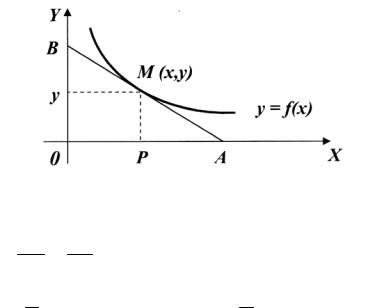
ЗАДАЧА 1. Найти кривую, обладающую тем свойством, что отрезок любой ее касательной, заключенный между осями координат, делится пополам в точке касания.

Пусть y = f (x) - уравнение искомой кривой, M (x, y) - произвольная точка кривой(рис. 1).

Рис. 1. Геометрическая интерпретация задачи

Угловой коэффициент касательной в этой точке равен y′. По условию AM = MB, т.е OP = PA = x, а значит, в любой точке М кривой

tg MAP = −y′ = xy ; следовательно, y′ = − xy .

Мы получили соотношение, связывающее неизвестную функцию y , независимую переменную x и производную от y по x , т. е. получили диффе-

4

ренциальное уравнение относительно y . Этому уравнению удовлетворяет функция y = cx , где С - любое число.

Действительно, если y = cx , то y' = − xc2 и − xy = − xc2 .

Таким образом, указанным выше свойством обладает бесчисленное множество кривых ("семейство" кривых), различающихся значениями постоянной С. Это - семейство равносторонних гипербол, асимптотами которых являются оси координат.

Для того чтобы из этого семейства кривых выделить одну определенную кривую, достаточно задать точку (x0 , y0 ) , через которую проходит эта кривая,

и определить соответствующее значение постоянной С.

Например, через точку (2,4) будет проходить та кривая семейства, для ко-

торой 4 = 2c , т.е. C = 8. Уравнение этой кривой y = 8x .

Дадим определения основных понятий.

Обыкновенным дифференциальным уравнением п-го порядка назы-

вается уравнение, связывающее независимую переменную, искомую функцию и ее производные:

F(x, y, y′, ... , y(n) ) = 0,

где F - функция, определенная в некоторой области, x - независимая переменная,

y - искомая функция переменной x, а y′, y′′, ... , y(n) - ее производные. При этом функция F может явно не зависеть от x, y, y′, ... , y(n−1) , но обязательно должна зависеть от y(n) .

Порядком дифференциального уравнения называется порядок старшей входящей в него производной.

Так, например,

5

Решением дифференциального уравнения называется всякая функция y = ϕ ( x ), подстановка которой в это уравнение обращает его в тожде-

Решение дифференциального уравнения, заданное неявно соотношением

Ф(x, y) = 0 , называют интегралом этого уравнения.

График решения дифференциального уравнения называется его инте-

гральной кривой.

2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА, РАЗРЕШЕННЫЕ ОТНОСИТЕЛЬНО ПРОИЗВОДНОЙ,

И ИХ ГЕОМЕТРИЧЕСКИЙ СМЫСЛ

ОСНОВНЫЕ ПОНЯТИЯ

Как уже было сказано, дифференциальным уравнением первого порядка

называется соотношение между независимым переменным, неизвестной функцией и ее производной.

Общий вид дифференциального уравнения первого порядка:

если соотношение (2.1) разрешить относительно y , то получится уравнение вида

если соотношение (2.1) разрешить относительно y′, то получится уравнение вида

Оно называется дифференциальным уравнением первого порядка, раз-

решенным относительно производной.

Дифференциальное уравнение первого порядка, разрешенное относительно производной, всегда можно записать в так называемой дифференциаль-

ной форме:

f (x, y)dx −dy = 0.

6

Наоборот, всякое уравнение вида (2.3), если Q(x, y) ≠ 0, можно разре-

Выясним геометрический смысл уравнения (2.2).

Пусть x и y - декартовы прямоугольные координаты точек плоскости, а y =ϕ(x) - решение данного уравнения. График этого решения – интегральная

кривая уравнения (2.2) есть непрерывная кривая, в каждой точке которой имеется касательная. Угловой коэффициент касательной к интегральной кривой в ее точке (x, y) равен y′, т.е. равен f (x, y). Таким образом, уравнение

y′ = f (x, y) дает связь между координатами точки и угловым коэффициентом касательной к интегральной кривой в этой точке. В каждой точке (x, y) области D, в которой определена функция f (x, y), мы можем вычислить у', т.е.

указать направление касательной к той интегральной кривой, которая проходит через эту точку. Построив в каждой точке области черточку ("стрелку"), наклоненную к оси ОХ под углом, тангенс которого равен получим

так называемое "поле направлений" (рис. 2).

Задать уравнение y′ = f (x, y) - значит задать в области D поле направ-

лений.

Решить это уравнение - значит найти кривую, касательная к которой в каждой ее точке совпадала бы с направлением поля в этой точке.

Рис. 2. Поле направлений

Таких кривых будет не одна, а целое семейство (построение можно начинать с любой точки данной области). Чтобы выделить определенную инте-

гральную кривую, нужно задать точку (x0 , y0 ) , через которую должна прохо-

7

дить кривая. При некоторых ограничениях на правую часть уравнения (2.2) через каждую точку области D будет проходить одна интегральная кривая.

Дифференциальное уравнение первого порядка вида y′ = f (x, y) имеет,

вообще говоря, не одно, а бесчисленное множество решений. Для того чтобы из этого бесчисленного множества решений выделить определенное решение,

обычно приходится задавать значение искомой функции y0 при некотором значении аргумента x0 . Пару чисел x0, y0 называют начальными условиями, или начальными данными, решения. Геометрически задание начальных условий равносильно заданию точки (x0 , y0 ) - "начальной точки" плоскости ХОУ. Будем говорить, что решение y =ϕ(x) уравнения y′ = f (x, y) удовлетворяет начальным условиям x0, y0 , если ϕ(x0 ) = y0 , т.е. если график этого решения проходит через точку(x0 , y0 ) .

Отыскание решения дифференциального уравнения y′ = f (x, y) , удовлетворяющего заданным начальным условиям x0, y0 , является одной из важней-

ших задач теории дифференциальных уравнений. Эта задача называется зада-

чей Коши.

Естественно, возникает вопрос: всегда ли существует решение задачи Коши и, если существует, будет ли оно единственным?

Ответы на эти вопросы дает теорема Коши - теорема существования и единственности решения дифференциального уравнения первого порядка, разрешенного относительно производной. Приведем ее формулировку.

Теорема Коши. Если функция f (xy) непрерывна в некоторой области D плоскости ХОУ и имеет в этой области непрерывную частную производную по f y′(x, y) , то, какова бы ни была точка (x0 , y0 ) области D , существует, и при-

том единственное, решение y =ϕ(x) уравнения y′ = f (x, y) , определенное в некотором интервале, содержащем точку x0 , принимающее при x = x0 значе-

ние ϕ(x0 ) = y0.

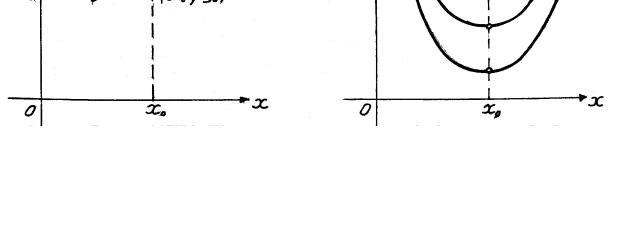
Геометрически это утверждение означает, что через каждую внутреннюю точку (x0 , y0 ) области D проходит, и притом только одна, интегральная кривая уравнения (рис. 3).

Из теоремы Коши следует, что в области D уравнение f y′(x, y) имеет бесчисленное множество решений. Действительно, считая x0 постоянным и изменяя значение y0 в некоторых пределах, получим для каждого значения y0 свое решение: y =ϕ(x, y0 ) (рис. 4).

Введем теперь следующие основные определения.

8

Функция y =ϕ(x, С) , зависящая от одной произвольной постоянной С, называется общим решением уравнения y′ = f (x, y) в некоторой области σ, ес-

ли она является решением этого уравнения для любого значения постоянной С (или для любого значения С из некоторого множества) и если любое решение уравнения, лежащее в области σ , может быть записано в виде при

конкретном значении С.

интегралом уравнения (2.1) в области σ.

Решения, получающиеся из общего при определенных значениях постоянной С, называются частными решениями данного уравнения. Аналогично определяются частные интегралы.

Геометрически общее решение (общий интеграл) уравнения (2.1) в об-

ласти σ представляет собой семейство интегральных кривых уравнения, обла-

дающее тем свойством, что каждая интегральная кривая, лежащая в области σ , принадлежит этому семейству кривых.

Если при этом функция f (x, y) , стоящая в правой части уравнения (2.2) области σ удовлетворяет условиям теоремы Коши, то через каждую точку (x0 , y0 ) области σ проходит одна определенная кривая семейства y =ϕ(x, C), (Φ(x, y, C) = 0). Соответствующее ей значение постоянной С можно определить, подставив координаты начальной точки (x0 , y0 ) в уравне-

ние y =ϕ(x, C), (Φ(x, y,C) = 0). Если y0 =ϕ(x0 , C0 ), (Φ(x0 , y0, C0 ) = 0) , то

интегральная кривая, проходящая через точку (x0 , y0 ) , будет иметь уравнение y =ϕ(x, C0 ), (Φ(x, y, C0 ) = 0).Эта кривая будет изображать частное решение уравнения (2.1), соответствующее значению С0. Таким образом, для выделения

9

из общего решения (интеграла) частного решения (интеграла) уравнения (2.2) достаточно задать его начальные условия.

ПРИМЕР: Уравнение y′ = 2 y разрешено относительно производной.

нены в верхней полуплоскости y 0. Через каждую ее точку проходит одно оп-

ределенное решение уравнения.

Основной задачей теории дифференциальных уравнений является отыскание всех решений данного дифференциального уравнения (в явной или неявной форме) и изучение свойств этих решений. Нахождение решений дифференциальных уравнений называют интегрированием этих уравнений.

Лекция 2

3. НЕКОТОРЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА, ИНТЕГРИРУЕМЫЕ В КВАДРАТУРАХ

Рассмотрим некоторые, наиболее важные типы дифференциальных уравнений первого порядка, интегрирование которых сводится к вычислению одного или нескольких неопределенных интегралов. Действие вычисления неопределенного интеграла, чтобы не было путаницы с термином "интегрирование уравнения", будем называть квадратурой

3.1. Уравнение вида y′ = f (x)

Уравнение вида y′ = f (x), где f (x) - функция, определенная и непрерывная на некотором интервале a x b оси ОХ .

Как известно из курса интегрального исчисления, все решения этого простейшего дифференциального уравнения исчерпываются соотношением

y′ = f (x) в полосе {a x b, −∞ y +∞}получаются из одной из них, например

y = ∫ f (x)dx , сдвигом, параллельным оси OY. Задавая в этой полосе любую точку M0 (x0 , y0 ), можно единственным образом определить постоянную

10