Учебники 80163

В зависимости от формы, в которой они представляют решения, эти методы делятся в основном на три группы:

1. Аналитические методы, дающие приближенные решения дифференциальных уравнений в виде аналитических выражений;

2.Графические методы, дающие приближенные решения уравнений в виде графиков;

3.Численные методы, дающие приближенные численные значения решений для указанных значений аргумента.

Эта классификация является в известной степени условной Так, например, приведенные ниже графические методы дают одновременно способы численного решения и т.д.

Рассмотрим некоторые из наиболее употребительных методов приближенного решения задачи Коши для дифференциальных уравнений первого порядка.

рывна и имеет непрерывную частную производную по y . Требуется найти решение уравнения (6.1), удовлетворяющее начальным условиям x0 , y0. По теореме Коши в некоторой окрестности точки (x0 , y0 ) такое решение существует и является единственным. Рассмотрим вспомогательное уравнение

с неизвестной функцией y = y(x) . Такое уравнение называется интегральным

(неизвестная функция входит под знак интеграла). Всякое непрерывное решение уравнения(6.2) (т. е. всякаянепрерывная функция, обращающая этоуравнение в тождество) является вместе с тем решением уравнения (6.1) с начальными условиями x0 , y0.

Действительно, если y = y(x) - непрерывнаяфункция, длякоторой

x

y(x) = y0 + ∫ f (x, y(x))dx,

x0

тоонадифференцируема:

21

т.е. функция y = y(x) . удовлетворяет уравнению (6.1) и начальным условиям

x0 , y0.

Таким образом, для решения поставленной выше задачи Коши достаточно найти непрерывное решение интегрального уравнения (6.2). С этой целью применим так называемый метод последовательных приближений. А именно, построим бесконечную последовательность непрерывных функций:

y0 ( x) = y0 ,

x

y1( x) = y0 + ∫ f (x, y0 )dx,

x0

x

y2 ( x) = y0 + ∫ f ( x, y1(x))dx,

x0

.......... .......... ....

x

yn −1(x) = y0 + ∫ f (x, yn −1(x))dx,

x0

.......... .......... ....

называемых соответственно нулевым, первым, вторым, ... п приближениями ре-

шения.

чальными условиями x0 , y0 в некоторой окрестности точки x0 может быть найдено с любой степенью точности, если положить y(x) ≈ yn (x), где n - достаточнобольшоечисло.

22

Метод последовательных приближений позволяет найти аналитическое выражение приближенного решения поставленной задачи Коши, т. е. является аналитическим методом. Оценка погрешности, получающейся от замены реше-

23

допущенная при этом погрешность удовлетворяет неравенству

Интегрируя уравнение y′ = y методом разделения переменных и опреде-

ляя по начальным условиям (0; 1) постоянную С, получим точное решение поставленной задачи Коши: y = ex.

Лекция 4

6.2. Метод Эйлера

Будем рассматривать задачу отыскания решения дифференциального уравнения

удовлетворяющего начальному условию y(x0 ) = y0 .

Известно, что при определенных условиях, например, если в некоторой окрестности точки (x0 , y0 ) плоскости ХОУ функция f (x, y) имеет непрерывную производную по y , эта задача имеет единственное решение.

Геометрически это означает, что при выполнении этих условий через точку (x0 , y0 ) проходит единственная кривая, являющаяся графиком решения

уравнения (6.3). Эта кривая называется интегральной кривой этого дифференциального уравнения.

Ввиду того, что решение уравнения (6.3) в явном виде удается найти не всегда, во многих практических задачах приходится искать приближенное решение. При этом часто достаточно знать приближенные значения искомой функции y(x) в отдельных точках. Составление таблицы приближенных зна-

чений решения задачи (6.3) для отдельных значений аргумента называют численным интегрированием дифференциального уравнения.

Существует много различных методов численного интегрирования дифференциального уравнения (6.3). Рассмотрим наиболее простые из них. Везде ниже предполагается, что для задачи (6.3) выполнены условия существования и единственности решения.

24

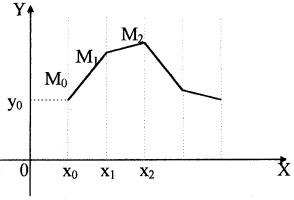
Метод Эйлера. Пусть требуется составить таблицу приближенных значений решения задачи (6.3) для равноотстоящих значений аргумента

x0 , x0 + h = x1, x0 + 2h = x2 и т.д.

Суть метода Эйлера заключается в том, что при достаточно малом значении шага h уравнение (6.3) на интервале [x0 , x0 + h]заменяется конечноразностным уравнением

Геометрически это означает, что интегральную кривую уравнения (6.3), проходящую через точку M0 (x0 , y0 ), заменяют отрезком касательной, проходящей через ту же точку (рис. 7). Из уравнения (6.4) мы находим приближенное значе-

x2 = x1 + h : y2 = y1 + f (x1, y1)h и т.д.

Погрешность метода Эйлера на каж-

дом шаге порядка h2 , но так как, вообще говоря, погрешности накапливаются, то при большом числе шагов приближенное значение может весьма значительно отличаться от точного. В связи с этим метод Эйлера, несмотря на всю его простоту, редко применяется в вычислительной практике.

Если большая точность не нужна, то можно рекомендовать следующее видоизменение метода Эйлера, при доста-

точно малом h делают один шаг по формуле (6.5). После того, как значение y1 в точке x1 = x0 + h найдено, остальные значения находят по формуле

точность которой несколько выше (порядка h3 ).

ПРИМЕР. Пользуясь формулой (6.6), составить таблицу приближенных

Вычисление будем вести по формуле (6.6), записанной в виде

yk +1 = yk −1 + 2∆yk ,

25

В силу сказанного выше погрешность будет порядка h3 = 0,001. Поэтому мы можем ручаться только за 2-3 знака в начале таблицы и за 1-2 знака в

где 0 θ 1. Отбрасывая в этой формуле остаточный член, мы можем написать приближенное равенство:

Значения y′(x0 ), y′′(x0 ), ... мы находим из уравнения (6.3), последовательно дифференцируя это уравнение.

Вычислив y1, мы по той же формуле (6.9) (заменив x0 , y0 соответственно на

x1 = x0 + h и y1) находим y2 и т.д.

Очевидно, метод Эйлера является частным случаем рассматриваемого метода при n =1. Погрешность этого метода на каждом шаге есть величина порядка hk +1.

26

y5 = y4 + ∆y4 и т.д. Таким образом диагональная табл. 4 может быть продолжена донужногозначения y(x). Дляконтролявычисленийнужноодновременносвычислением ∆yk поформуле(6.11) вычислить ∆yk по формуле

Так как эта формула, как и формула (6.11), приближенная, то ∆yk , вычисленные по этой формуле, могут отличаться в последних знаках от ∆yk , вычисленных

поформуле (6.11).

Для применения метода Адамса, как мы видим, кроме данных значений x0 , y0 нужно знать еще три значения y1, y2 , y3 функции y(x) . Эти значения могутбытьнайдены, например, при помощи формулы Тейлора (метод II).

28

Формулы (6.11) метода Адамса, как уже отмечалось, дают на каждом шаге погрешность вычисления порядка h4. Поэтому если необходимо получить значения y сточностьюдо10−n , тошаг h выбираютизнеравенства h 10−n .

Ведя вычисления с одним - двумя запасными знаками, следят за ходом

третьих конечных разностей ∆3q , добиваясь того, чтобы они оставались практически постоянными, т.е. отличались не более чем на одну - две единицы заданного

разряда. Наоборот, если задан шаг таблицы h , то неравенство h 10−n позволяет оценить погрешность результата. При этом вычисления надо вести с одним - двумя лишнимизнаками, округляя полученные значения до нужного разряда.

ПРИМЕР. Пользуясь методом Адамса, продолжим таблицу значений y для задачи (6.7), используя полученные в примере 2 значения y1, y2 , y3 .

Составляем табл. 5 конечных разностей q .

29