3.3. Вычисление длин дуг плоских кривых

Если линия – это график функции где 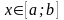, то длина дуги этой линии, вычисляется по формуле 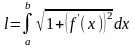, где функция на рассматриваемом отрезке – непрерывно-дифференцируема.

Пример 19. Вычислить длину дуги линии 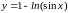, где .

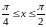Используем формулу длины дуги , тогда получим:

.

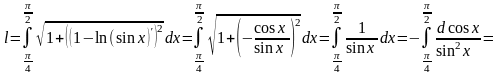
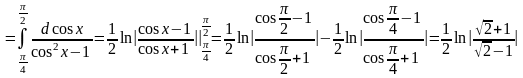4. Дифференциальные уравнения

4.1. Понятие дифференциального уравнения

Уравнение, содержащее неизвестную функцию, ее аргументы, производные или дифференциалы искомой функции, называется дифференциальным уравнением. Если искомая функция зависит от одного аргумента, то уравнение называется обыкновенным дифференциальным уравнением:

.

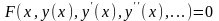Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение. Например, 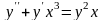– обыкновенное дифференциальное уравнение второго порядка.

Дифференциальным уравнением первого порядка называется уравнение (или для упрощения записи 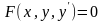). Уравнение может быть записано через дифференциалы .

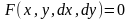Некоторые уравнения первого порядка разрешимы относительно производной и могут быть записаны в виде

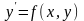. (4.1)

4.2. Понятие общего решения дифференциального уравнения

Общим решением дифференциального уравнения (4.1) называется функция вида

, (4.2)

которая зависит от переменной и от произвольной постоянной 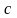и при подстановке в уравнение (4.1) обращает его в тождество.

4.3. Понятие частного решения дифференциального уравнения

Частным решением дифференциального уравнения (4.1) называется решение, которое получается из общего (4.2) при каком-либо определенном значении произвольной постоянной .

Задачей Коши называют задачу нахождения такого частного решения 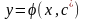уравнения (4.1), которое удовлетворяет заданному начальному условию 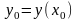, т.е. значение произвольной постоянной 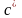определяется условием 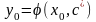. График частного решения называется интегральной кривой.

Общее решение (4.2) дифференциального уравнения (4.1) на плоскости 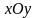это множество интегральных кривых, а каждому частному решению уравнения (4.1) соответствует одна из них. Если частное решение определяется начальным условием , то интегральная кривая проходит через точку .

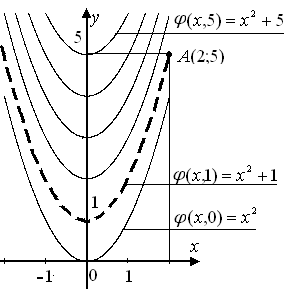Решениями дифференциального уравнения 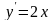, очевидно, являются функции 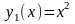, , 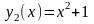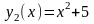и т.д., которые можно коротко записать в виде 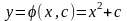– это и есть общее решение, а интегральные кривые на плоскости – параболы (см. слева).

Для определения интегральной кривой, проходящей через точку 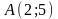, найдем значение произвольной постоянной из условия: , в нашем случа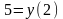е: , т.е. 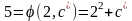, следовательно, . Соответствующее частное решение имеет вид 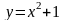, его график обозначен на рисунке штриховой линией.

4.4. Дифференциальные уравнения первого порядка с разделяющимися переменными

Если дифференциальное уравнение может быть представлено в виде (4.1), где правая его часть допускает представление в виде произведения: 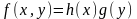, то такое уравнение называется уравнением c разделяющимися переменных. Такое уравнение можно привести к виду, где разные переменные сгруппированы в разных частях равенства

,

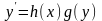
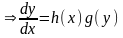
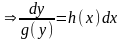последнее уравнение называется уравнением в разделенных переменных.

Замечание. В процессе деления на 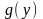необходимо чтобы 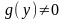, т.к. имеется возможность потерять решени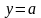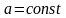е ( ), где 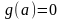– тогда необходимо отдельно проверить является ли функция решением исходного уравнения.

Пример 20. Найти общее решение дифференциального уравнения .

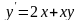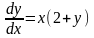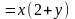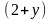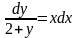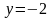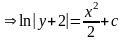
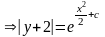
Представим уравнение в виде , где правая часть представлена в виде произведения , т.е. исходное уравнение, при делении его допускает разделение переменных (далее проверить, что есть решение уравнения). Проинтегрируем последнее уравнение: 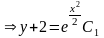, т.е.

. Если 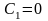, то получим потерянное решение .

Дифференциальное уравнение с разделяющимися переменными может быть задано в виде

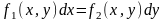, (4.3)

где функци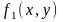и и 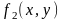тоже могут быть представлены в виде произведения функций , :

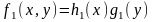. (4.4)

Чтобы решить уравнение (4.4) необходимо выполнить разделение переменных, для этого выполним деление обеих его частей на произведение . Получим уравнение в разделенных переменных:

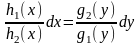. (4.5)

Интегрируя обе части уравнения (4.5), получим общее решение

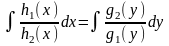. (4.6)

Пример 21. Найти общее решение дифференциального уравнения .

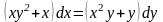Представим уравнение в виде 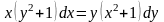, очевидно, это уравнение вида (4.4). Разделим обе его части на произведение 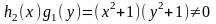: 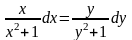, отсюда 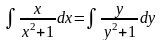. Вычислим каждый из интегралов:

,

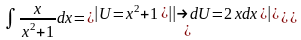аналогично, .

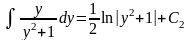Общее решение (4.6) имеет вид: 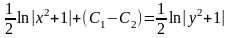, умножим обе части на 2 и представив 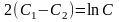, получим 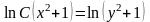, откуда .

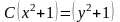
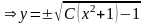Пример 22. Найти частное решение дифференциального уравнения удовлетворяющее начальному условию .

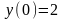Решение состоит из двух этапов.

1 этап. Определяется общее решение дифференциального уравнения. См. пример 21, в котором оно было найдено: .

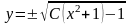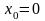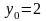2 этап. Из общего решения определяется то единственное, которое соответствует начальному условию , т.е. при и >0 определяется значение постоянной : .

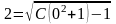
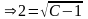
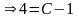
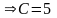Итак, частное решение имеет вид .