2.5. Интегрирование по частям в определенном интеграле

Если для вычисления интеграла требуется применить формулу интегрирования по частям , где функции и непрерывно-дифференцируемы на , то используя формулу Ньютона-Лейбница, получим

. (2.5)

Пример 13.

=

Пример 14.

= = .

3. Приложения определенного интеграла

3.1. Вычисление площадей в декартовых координатах

1 ) Если плоская фигура ограничена сверху графиком функции , снизу осью , слева и справа прямыми и , то ее площадь вычисляется по формуле

. (3.1)

2) Если плоская фигура ограничена справа графиком функции , слева осью , сверху и снизу прямыми и , то ее площадь вычисляется по формуле

. (3.2)

3 ) Если плоская фигура ограничена сверху графи-ком функции , снизу графиком функции , слева и справа прямыми и , то ее площадь вычисляется по формуле

. (3.3)

Если фигура ограничена прямыми , ( ) и графиками функций и ( на ), то для вычисления площади получаем формулу, аналогичную (3.3):

. (3.4)

Пример 15. Вычислить площадь фигуры, ограниченной линиями и .

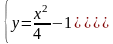
Р ешение. Укажем на рисунке фигуру, площадь которой нужно вычислить, определив для этого точки пересечения линий:

и .

Из указанных выше формул вычисления площади выберем формулу (3.3), т.к. фигура ограничена сверху и снизу кривыми и , а слева и справа прямыми , , проходящими через точки пересечения этих кривых:

(кв. ед.).

Пример 16. Вычислить площадь фигуры, ограниченной параболами

и , где .

Чтобы построить параболы, приведем их к каноническому виду

Изобразим фигуру (см. рис. слева) – искомая площадь между параболами и осью заштрихована. Вычислять площадь в данном случае проще, если переменной интегрирования считать , иначе фигуру придется разбивать на несколько частей.

Заметим, что искомая площадь может быть определена как разность площадей, образуемых с осью параболой (2) – и параболой (1) – . Определив точки пересечения парабол с осью , применим формулу (3.4): =

3 .2. Вычисление объемов тел вращения

Если плоская фигура сверху ограничена графиком функции , снизу осью , слева и справа прямыми и , то объем тела, полученного вращением этой фигуры вокруг оси , находится по формуле

. (3.5)

Если плоская фигура справа ограничена графиком функции , слева осью , сверху и снизу прямыми и , то объем тела, полученного вращением этой фигуры вокруг оси , находится по формуле

. (3.6)

Пример 17. Найти объем тела, полученного вращением вокруг оси плоской фигуры, ограниченной линиями и .

Первая линия является прямой, вторая параболой, найдем точки, в которых линии пересекаются. Для этого решим систему уравнений:

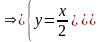
Изобразим тело вращения, заштриховав вращаемую фигуру.

Объем всего тела вращения вокруг оси равен разности объемов – , полученного от вращения треугольника, и , полученного от вращения криволинейного треугольника, ограниченного сверху дугой параболы: .

Пример 18. Найти объем тела, полученного вращением вокруг оси плоской фигуры, ограниченной линиями и , где .

Первая линия является эллипсом, вторая параболой. Найдем точки, в которых линии пересекаются. Для этого решим систему уравнений:

Изобразим тело вращения, заштриховав вращаемую фигуру.

Объем всего тела вращения вокруг оси равен сумме объемов верхней части – и нижней части – . Для вычисления объемов и , применим формулу (3.6):

.