
- •Неопределенные и определенные интегралы
- •Введение
- •1.2. Основные свойства неопределенного интеграла.
- •1.3. Таблица основных интегралов.
- •1.4. Интегрирование заменой переменной.
- •1.5. Интегрирование по частям.
- •2. Определенный интеграл
- •2.1. Понятие определенного интеграла
- •2.2. Основные свойства определенного интеграла
- •2.3. Вычисление определенного интеграла
- •2.4. Замена переменной в определенном интеграле
- •2.5. Интегрирование по частям в определенном интеграле
- •3. Приложения определенного интеграла
- •3.1. Вычисление площадей в декартовых координатах
- •3 .2. Вычисление объемов тел вращения
- •3.3. Вычисление длин дуг плоских кривых
- •4. Дифференциальные уравнения
- •4.1. Понятие дифференциального уравнения
- •4.2. Понятие общего решения дифференциального уравнения
- •4.3. Понятие частного решения дифференциального уравнения
- •4.4. Дифференциальные уравнения первого порядка с разделяющимися переменными
- •Варианты контрольных заданий Задания для самостоятельной работы.
- •Оглавление
- •Неопределенный и определенный интегралы
- •394006 Воронеж, ул. 20-летия Октября, 84
1.5. Интегрирование по частям.
Пусть
 и
и
 две дифференцируемые функции.
Найдём дифференциал от их произведения:
две дифференцируемые функции.
Найдём дифференциал от их произведения:
 ,
или, что тоже самое,
,
или, что тоже самое,
 .
Проинтегрируем полученное равенство:
.
Проинтегрируем полученное равенство:
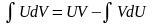 . (1.2)
. (1.2)
Формула
(1.2) называется формулой интегрирования
по частям, она применяется, в основном,
если под знаком интеграла находится
произведение многочлена
 на одну из функций
на одну из функций
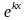 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
Причем, для получения положительного
результата нужно руководствоваться
следующим правилом выбора функции
.
Причем, для получения положительного
результата нужно руководствоваться
следующим правилом выбора функции
 и дифференциала
и дифференциала
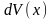 :
:
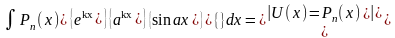 ;
;
 .
(1.3)
.
(1.3)
Пример
6. Вычислить интеграл
 .
.
Согласно
правилу (1.3)
 :
:
 =
=


Пример 7.




Иногда применение формулы (1.2) позволяет выразить искомый интеграл через самого себя, тогда в процессе решения имеем уравнение относительно этого интеграла, решая которое, получаем ответ к примеру.
Пример 8.

 =
=
 ,
то есть:
,
то есть:



 ,
,
откуда находим
 +С.
+С.
2. Определенный интеграл
2.1. Понятие определенного интеграла
Предположим,
что на отрезке
 задана непрерывная функция
задана непрерывная функция
 .
Разобьем отрезок
на n частей точками
деления
.
Разобьем отрезок
на n частей точками
деления
 ,
при условии
,
при условии .
В каждом из отрезков
.
В каждом из отрезков
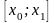 ,
,
 …
…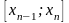 возьмем по точке, которые обозначим
возьмем по точке, которые обозначим
 ,
,
 ,...,
,...,
 ,
и вычислим в них значения функции
,
и вычислим в них значения функции
 ,
,
 ,…,
,…,
 .
Составим сумму, которая называется
интегральной суммой для функции
на отрезке
:
.
Составим сумму, которая называется
интегральной суммой для функции
на отрезке
:
 ,
,
где
 ,
,
 .
.
Определение.
Если при любых разбиениях отрезка
точками
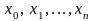 ,
такими что
,
такими что
 ,
и при любом выборе точек
,
и при любом выборе точек
 на отрезках
на отрезках
 ,
,
интегральная сумма
,
,
интегральная сумма
 стремиться к одному и тому же пределу
(числу), то этот предел и называется
определенным интегралом от функции
на отрезке
и обозначается
стремиться к одному и тому же пределу
(числу), то этот предел и называется
определенным интегралом от функции
на отрезке
и обозначается
 ,
т.е.
,
т.е.
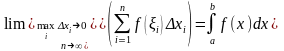 .
(2.1)
.
(2.1)
Число
 называется нижним пределом интегрирования,
называется нижним пределом интегрирования,
 – верхним пределом.
– верхним пределом.
Замечание. Доказано, что в наших предположениях о непрерывности функции на отрезке предел в левой части формулы (2.1) существует, т.е. определенный интеграл от непрерывной функции на отрезке существует.
2.2. Основные свойства определенного интеграла
1)
Определенный интеграл не зависит от
переменной:
 ;
;
2)
 ; 3)
; 3)
 ; 4)
; 4)
 ;
;
5)
Интеграл от суммы (разности) функций
равен сумме (разности) интегралов от
этих функций:
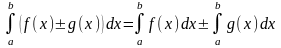 ;
;
6)
Для любого
 :
:
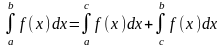 ;
;
7)
Для четных (нечетных) функций

2.3. Вычисление определенного интеграла
Для вычисления определенного интеграла пользуются формулой Ньютона-Лейбница:
 , (2.2)
, (2.2)
где – непрерывная на функция, – любая из первообразных .
Пример 9.

 .
.
Пример
10.
 .
.
2.4. Замена переменной в определенном интеграле
При
вычислении определенного интеграла
требуется вычислять первообразную
функции
,
а если интеграл не указан среди табличных,
то, как и в неопределенном интеграле,
применяется замена переменной. Следует
обратить внимание на то, что замена
затрагивает пределы интегрирования,
т.е. если
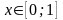 ,
то при замене
,
то при замене
 новая переменная
новая переменная
 .
.
Если замена имеет вид , то
 , (2.3)
, (2.3)
где
 и
и
 находятся из условий
находятся из условий
 ,
,
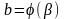 .
После замены переменной и изменения
пределов интегрирования возвращаться
к исходной переменной не нужно.
.
После замены переменной и изменения
пределов интегрирования возвращаться
к исходной переменной не нужно.
Замечание.
Замена
только тогда выполняется корректно,
если функция
является непрерывно-дифференцируемой
на отрезке
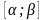 .
.
Пример 11.
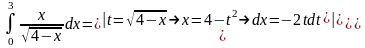 =
=
 .
.
Пример 12.
 =
=
 .
.
