1.2. Основные свойства неопределенного интеграла.

1. Неопределённый интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций:

.

2. Постоянный множитель можно выносить за знак неопределённого интеграла, т.е. ( – const).

3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого: .

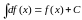4. Производная неопределённого интеграла равна подынтегральной функции: .

5. Дифференциал неопределённого интеграла равен подынтегральному выражению: .

1.3. Таблица основных интегралов.

1.	8.
2.	9.
3.	10.
4.	11.
5.	12.
6.	13.
7.

Замечание. Табличные формулы инвариантны относительно замены переменной, т.е. остаются справедливыми, если переменную заменить любой другой переменной или дифференцируемой функцией .

Пример 1. Вычислить интеграл .

Применяя свойства интеграла 1, 2 и формулы 2 и 3 таблицы интегралов, получим

Пример 2. Вычислить интеграл .

.

При нахождении интеграла использовалась формула 4 таблицы интегралов.

1.4. Интегрирование заменой переменной.

Если нельзя найти непосредственно, используя свойства и таблицу интегралов, то преобразуют подынтегральное выражение, заменяя переменную интегрирования. Это можно сделать двумя способами – либо переменную заменяют функцией, зависящей от другой переменной ( ), либо какое-нибудь выражение, зависящее от , считают новой переменной :

(1.1)

Оба пути решения ведут, как правило, к упрощению подынтегрального выражения, чтобы полученный интеграл стал табличным или раскладывался на сумму табличных. После вычисления полученного интеграла возвращаются к старой переменной. Основан метод на свойстве инвариантности формул интегрирования.

Пример 3. Вычислить интеграл .

Заметим, . Подынтегральное выражение выражается через функцию 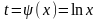, тогда получим интеграл , который имеется среди табличных интегралов: . Далее выполним обратную замену переменных: .

Итак, коротко, получим = .

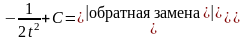
Пример 4. Вычислить интеграл .

Здесь можно обозначить через новую переменную подкоренное выражение, т.к. его производная , с точностью до множителя, является множителем подынтегрального выражения, т.е.

= = =

.

Пример 5. Вычислить интеграл .

Подынтегральное выражение является неправильной дробью, интегрирование которой следует начать с выделения целой части в дроби:

.

Проинтегрируем .

Последний интеграл есть среди табличных: .

А в интеграле введем замену переменной 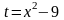, заметив, что производная содержится в числителе, с точностью до коэффициента:

.

Получим: = .