
Учебное пособие 800347
.pdf
Обозначая выражения при неизвестных в виде соответствующих коэффициентов:
|
|
a |
1cth( Lz1 ) ; |
|
|
||
|
|
b |
|
1 / sh( Lz1 ) ; |
|
|
|
|
|
c |
|
1 / sh( Lz1 ); |
|
|
|
d |
i cth |
Lzi |
Lz i |
1 |
i 1cth Lz i 1 Lzi |
; |
|
|
|
e |
i 1cth |
Lz i 1 Lzi |
; |
(3.28) |
|
|
|
f |
N / sh |
|
LzN Lz(n 1) |
; |
|
|
g |
N cth LzN |
Lz N 1 |
экв ; |
|
||
v 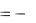 ,
,
перепишем систему (3.26) в более кратком виде
|
a 1 Lz0 |
b 1 Lz1 |
v 0 ; |
|
||
c i Lz i |
1 d |
i Lzi |
e i |
1 Lz i 1 |
0 ; |
(3.29) |
f |
N 1 Lz N 1 |
g N LzN |
0. |
|
||
Матрица коэффициентов этой системы трехдиагональная, поэтому для решения воспользуемся методом прогонки /22,113,140/

|
N LzN |
frN 1 g fh N 1 , i N ; |
||
|
|
|
|
|
|
i Lzi |
hi i 1 Lz i 1 ri , i (N 1),0 , |
||
где 0 Lz0 |
1 Lz0 , а ri и hi определяются следующим образом: |
|||
b h1 a ;
r |
|
|
v |
; |
|
|
|
|
|
|
|
||||
1 |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
h i |
|
|
|
e |
; |
||
|
|
|
|
|
|
||
|
d |
chi 1 |
|||||
|
|
|
|||||
r |
|
|
|
cri 1 . |
|
||
i |
d |
chi 1 |
|
|
|||
|
|
||||||
(3.30)
(3.31)
(3.32)
(3.33)
(3.34)
(3.35)
Рассчитав необходимые значения i Lzi , по (3.22) и (3.24) ана-
лизируем температурные поля всех КТС, входящих в данную конструкцию. Для КТС, состоящих из одной ТМ1, подставляя (3.22) в соот-
ветствующие граничные условия, находим аналитические выражения для
1 Lz 0 и 1 Lz1 |
, используя которые, получим более простое выражение |
|
|||||||||||||||
|
cos |
n x |
cos |
m y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.(3.36) |
||
x, y, z |
|
Lx |
Ly |
|
1 |
|
экв sh Lz |
|
ch z |
1 |
|
|
sh z |
||||
|
Lx Ly Kn Km |
|
|
|
|
sh Lz |
|
|
|
|
|
|
|||||
|
|
1 sh2 L |
|
|
1 sh2 Lz |
|
/ / |
|
|||||||||
n 0 m 0 |
|
|
|
|
|
экв |
|
|
|||||||||
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
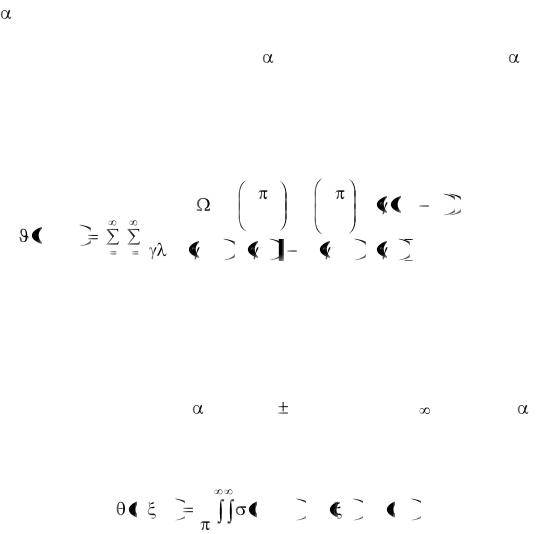
Моделирование температурных полей микроплаты (подложки), кристалла ИС или дискретного АК, а также МЭУ в целом (когда нет информации о конкретной системе охлаждения для данного устройства, т.е. не определено экв), рассматриваемых в этом случае относительно внешней температуры (корпуса, теплоотвода, окружающей среды), приводит к краевой задаче,
содержащей уравнения (3.1), (3.4) при u = 0, (3.6) при q = q(x,y) и z = 0,
(3.8). Полученную систему уравнений решаем методом конечного косинуспреобразования Фурье с собственными функциями, аналогичными предыдущей задаче. Выражение для температурного поля микроплаты (кристалла) имеет следующий вид /91/:
|
cos |
n x |
cos |
n |
|
sh Lz z |
|
|
|
L y |
|||||
x, y, z |
|
L x |
|
. (3.37) |
|||
|
|
|
|
|
|
||
n 0m 0 |
ch Bz ch z 1 th Bz |
th z L x L y K n K m |
|||||
В случае, когда размерами подложки или кристалла можно пренебречь (интегральные или бескорпусные навесные АК, пленочные элементы, которые удалены от краев на определенное расстояние, обусловленное принципом местного влияния /23/) или они неизвестны (оценка ТР на этапах функционального проектирования), переходим к ТМ2. Тогда для подобной краевой задачи ((3.1), (3.4) при u = 0, u = 0,5Lu.кт и Lu.п 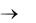 , (3.6) при z = 0 и (3.8)) решение требует использования метода интегрального преобразования Фурье в бесконечных пределах /111,112/
, (3.6) при z = 0 и (3.8)) решение требует использования метода интегрального преобразования Фурье в бесконечных пределах /111,112/
z, , x |
2 |
x, y, z cos x cos xy dxdy ; |
(3.38) |
|
|||
|
|||
|
|
0 0 |
|
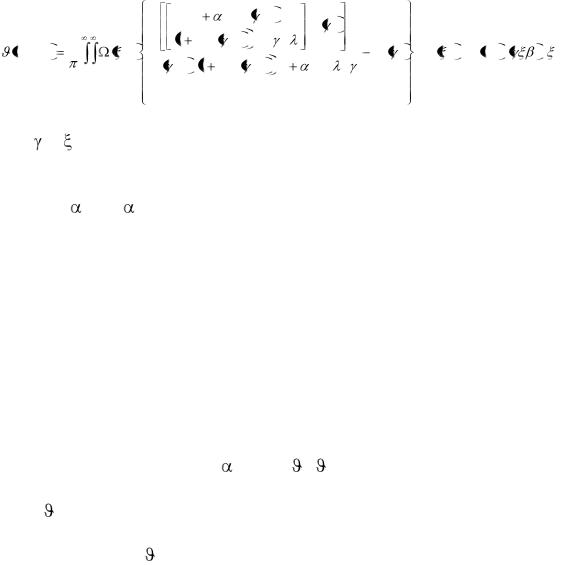
После преобразований по формуле обращения /111,112/ получаем выражение, описывающее температурное поле компонента или элемента на подложке:
|
|
|
1 |
эквsh Lz |
ch |
z |
|
|||||
|
2 |
|
|
|
1 sh2 |
Lz |
1/ 2 |
: / |
d dx ,(3.39) |
|||
x, y, z |
|
, x |
|
|
|
sh z cos x cos xy / |
||||||
|
|
|
|
|
|
|
|
|||||
|
|
sh Lz / 1 |
sh2 |
Lz |
1/ 2 |
|
/ / |
|||||
|
|
|
|
|
|
|
||||||
|
0 0 |
|
|
экв |
|
|
||||||
где = [ 2 + x2]1/2.
Для определения входящих в уравнения краевых задач коэффициентов или экв рассматриваются три случая теплообмена: конвективный (поверхности конструкции МЭУ, соприкасающиеся с газовой или жидкой средой), излучением, кондуктивный ( поверхности, контактирующие с другими частями конструкции).
Конвективный коэффициент теплоотдачи определяется с помощью критериального уравнения подобия /16,23,29,138/
Коэффициент теплоотдачи излучением рассчитывается на основании соотношений, базирующихся на использовании закона Стефана-Больцмана
/23,29/.
При наличии теплоотводящих устройств (например, радиаторов) определяется эквивалентный коэффициент теплоотдачи /53/
|
|
экв = P/[ 3( т (x,y,z))Sт], |
(3.40) |
где |
3 - заданное значение перегрева (среднее, максимальное, в термокри- |
||
тичной области |
и т.д.), вычисляемое по выражению для температурного |
||
поля теплоотвода |
т(x,y,z); |
|
|

Sт - площадь его основания;
P - рассеиваемая мощность.
Величина экв зависит от конструкции теплоотвода, применяемых материалов, вида охлаждения. Ее определение основано на анализе температурных полей конструктивных элементов теплоотвода, отводящих тепло (ребер, штырей, пластин, каналов с теплоносителем и т.д.) /23,138/.
Процесс кондуктивного теплообмена приходится рассматривать в следующих случаях:
микроплата приклеена к корпусу; кристалл припаян или приклеен к корпусу ИС или подложке;
устройство (корпусированные и бескорпусные ГИС, МСБ, МКМ и др.) приклеено или прижато к плате или теплоотводящей поверхности;
зазоры между соответствующими КТС, корпусом и платой меньше 5 мм (конвекция отсутствует или пренебрежимо мала /23,138/).
Здесь необходимо переходить к краевой задаче с граничными условиями первого рода (3.8), для которой получено решение (3.34), или исполь-
зовать следующее значение /6/: |
|
|
|
= с / с , |
(3.41) |
где |
с , с - коэффициент теплопроводности материала и толщина соедини- |
|
тельного слоя или зазора. |
|
|
При необходимости учета теплоотвода через выводы и крышку корпуса в экв входят дополнительные слагаемые, которые определяются из
(3.17)-(3.18):
в |
в m |
|
B |
th mLв |
, |
(3.42) |
экв |
1 |
Bth mL в |
||||
|
|
|
|
|||

кк |
|
m |
|
B |
th mL kk.z |
. |
(3.43) |
|
экв |
кк |
1 |
Bth mL kk.z |
|||||
|
|
|
||||||
|
|
|
|
|
||||
Полученные соотношения (3.25), (3.35) и (3.36) могут быть использованы и для устройств и приборов в корпусах круглой формы (тип 3 для ИС и МСБ), при этом они заменяются эквивалентным квадратом со стороной L = R 1/2, где R - радиус корпуса.
Для более детального и строгого анализа температурных полей в этих конструкциях целесообразно рассматривать такую задачу в цилиндрической системе координат (r, ,z), тогда при условии симметрии температурного поля уравнение (3.1) примет вид
2 |
1 |
|
2 |
|
|
||||
|
|
|
|
|
0 . |
(3.44) |
|||
|
|
|
|
|
|
|
|
||
|
r 2 r r |
|
z2 |
||||||
|
|
|
|
||||||
Граничные условия включают (3.5) при Lu = R, (3.6) при |
z = 0 и (3.8). |
||||||||
Решение осуществляется с помощью интегрального преобразования Ханкеля по координате r /112/, использующего в качестве собственной функцию Бесселя первого рода нулевого порядка J0 /112/. Применяя для вычислений, входящих в формулу обращения функций Бесселя нулевого J0 и первого порядка J1, интегральные представления /126/, запишем решение в окончательном виде
|
|
|
|
|
|
|
|
|
|
|
|
/ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
r n |
|
sin |
sin 3 d |
||
|
6q |
|
|
|
Lz |
z |
/ 2 |
r n |
|
|
|
R |
||||||
|
|
|
|
|
|
|
|
|
|
,(3.45) |
||||||||
r, z |
r |
sh |
n |
cos |
sin |
d |
|
0 |
|
|
||||||||
2 |
|
R |
|
R |
|
n Lz |
|
/ 2 |
|
|
2 |
|
||||||
|
|
n 1 |
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 ch |
|
sin |
|
sin sin 3t d |
|||
|
|
|
|
|
|
|
|
|
|
|
|
n |
||||||
|
|
|
|
|
|
|
|
|
|
|
n |
R |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

где r - радиус или эквивалентный радиус ИТ; n - решение уравнения J0( n) = 0 /173/.
3.2.2.2. Нестационарные задачи
Моделирование температурных полей ИС, интегральных и дискретных АК требует учета реальных временных и частотных режимов работы, т.е. вида конкретных сигналов, что приводит к нестационарным задачам с зависимыми от времени тепловыми потоками q(x,y,t). В случае комбинации различных граничных условий, содержащих разные координатные и временные зависимости перегревов и тепловых потоков, решения таких задач для объемных температурных полей записываются в виде тройных рядов Фурье /111,112/, что может затруднять вычисления и увеличивать затраты времени.
Учитывая высокую теплопроводность кремния и материалов корпусов
/5,16,23,26,28,29,32,48,58,65,66,72,84,138/ и расположение областей макси-
мальных перегревов на поверхности кристаллов, упростим задачу для случая ИТ с произвольными зависимостями q(x,y,t) путем перехода к двумерной постановке, которая включает уравнение (3.1) для координат x и y, дополненное в правой части слагаемым q(x,y,t)/Lz, а также практически важные случаи граничных условий: (3.4) при u = 0 (адиабатические) или (3.5) при u.3 = 0 (нулевые) и начальное условие (3.9).
С помощью преобразования (3.20) уравнение (3.1) сводится к обыкновенному дифференциальному уравнению для изображения (t), решение которого, выраженное через экспоненциальные функции /112,126/ и подставленное в соответствующую формулу обращения /112/, позволяет получить искомое выражение для температурного поля в общем виде (любые функции q(x,y,t)) при условиях (3.4) - собственные функции cos(n u/Lu), и (3.6) - sin(n u/Lu):
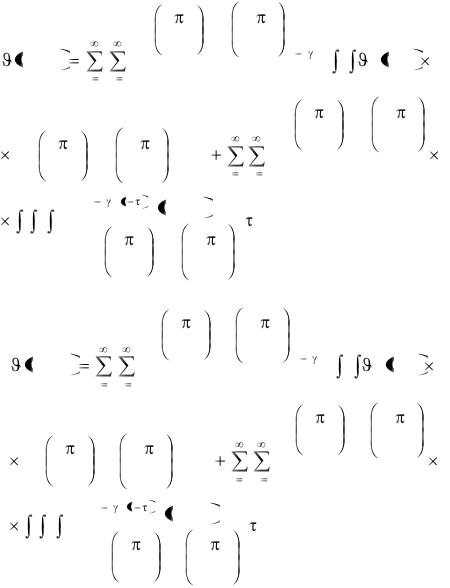
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
n x |
|
cos |
m y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L x |
|
|
|
L y |
|
|
|
a |
2 |
t |
Lx Ly |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x, y, t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
x, y |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L x L y K nm |
|
|
|
|
|
|
|
|
н |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
n 0 m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
n x |
|
cos |
m y |
|
|
|
|||||||||||
cos |
|
n x |
cos |
|
|
m y |
|
dxdy |
|
|
|
|
|
|
L x |
L y |
; |
(3.46) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
L x |
|
|
|
L y |
|
|
|
n 0 m 1 |
|
|
|
|
|
L x L y K nm |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
t Lx Ly |
e |
|
a 2 |
|
t |
|
|
q x, y, t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 0 |
0 Lz cos |
n x |
|
|
cos |
m y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
L y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
L x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
n |
x |
sin |
m y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L x |
L y |
|
|
|
|
|
|
2 |
Lx Ly |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x, y, t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e a |
t |
|
|
x, y |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L x L y K nm |
|
|
|
|
|
|
н |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
n 0 m 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
n |
|
|
x |
sin |
|
m y |
|
|
|
||||||
sin |
|
|
n x |
|
sin |
|
|
m y |
|
|
dxdy |
|
|
|
|
|
|
|
|
L x |
|
L y |
; |
(3.47) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
L x |
|
|
|
L y |
|
|
|
|
n 0 m 1 |
|
|
|
|
|
L x L y K nm |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
t Lx Ly |
e |
a |
2 t |
q x, y, t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0 0 |
|
|
0 Lz |
sin |
|
n x |
|
|
sin |
|
m y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
L x |
|
|
|
|
L y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
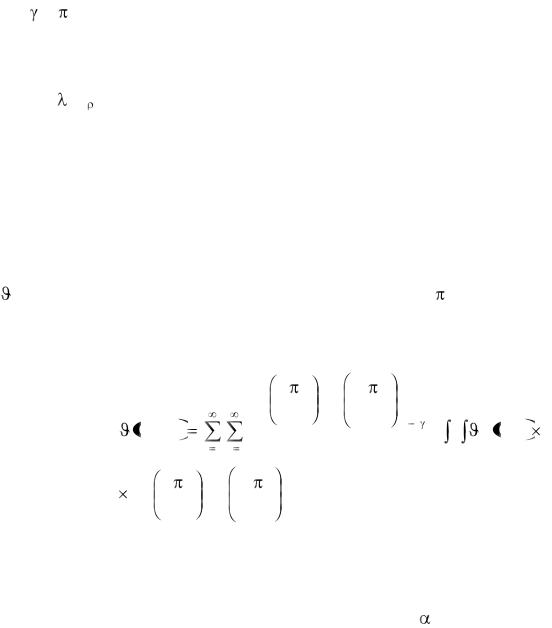
где = [(n/Lx)2 + (m/Ly)2]1/2;
Knm = 1 при n = m = 0;
Knm = 0,5 при n(m) = 0 и m(n) > 0; Knm = 0,25 при n > 0 и m > 0;
a = /(c ) - температуропроводность материала ТМ.
При работе АК в режиме, когда выделение тепловой энергии происходит в течение дискретных повторяющихся (периодических или апериодических) временных интервалов (например, в случае импульсных сигналов с большой скважностью, гармонических сигналов низкой частоты и т.п.), необходимо знать остаточное значение перегрева к началу следующего рабочего интервала. Для этого решается задача на охлаждение при заданном начальном распределении перегревов: (3.1), (3.5), (3.8) при z = Lz и z = 0, (3.9) с
н(x,y). Собственными функциями здесь будут sin(n u/Lu) /112/, используя для решения такой задачи соответственно синус-трансформанту Фурье /112/, получим
|
|
|
|
sin |
n x |
sin |
m y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lx Ly |
|
|
||||
|
|
|
|
|
|
L x |
L y |
|
|
2 |
|
|
||
x, y, t |
|
|
|
|
e a |
t |
|
x, y |
||||||
|
|
|
0.25L x L y |
|
|
|
н |
|||||||
|
|
n 0 m 0 |
|
|
|
0 0 |
|
(3.48) |
||||||
sin |
n x |
sin |
m y |
dxdy. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
L x |
L y |
|
|
|
|
|
|
|
|
|
|||
Рассмотрим задачу моделирования трехмерного температурного поля по уравнению (3.1) в упрощенной постановке, а именно, для случая нулевых граничных условий (3.4) и (3.8), условии (3.6) при z = 0 и нулевом началь-
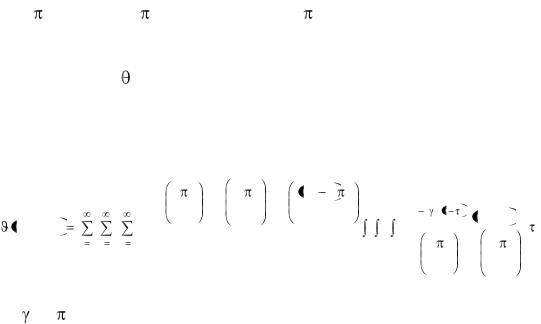
ном условии (3.9). Находим соответствующие собственные функции /112/: cos(n x/Lx), cos(m y/Ly) и cos( (2k-1) z/2Lz), применяем к данной системе конечные интегральные косинус-преобразования по трем пространственным координатам, переходим к обыкновенному дифференциальному уравнению по времени для (t), решением которого являются экспоненты /112/. По трехмерной формуле обращения, аналогичной (3.21), окончательно получаем следующую зависимость:
|
|
cos |
n x |
cos |
|
m y |
cos |
|
2k 1 |
z |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
t Lx Ly |
e a 2 t |
|
|
|
|||||||
x, y, z, t |
a |
Lx |
|
Ly |
|
2Lz |
|
|
q x, y, t |
|
d dxdy ,(3.49) |
||||||||||
|
L |
|
L |
L |
K |
|
|
|
|
|
|
|
n x |
|
m y |
|
|||||
|
n 0m 0 k 1 |
z |
nm |
|
0 0 0 |
|
|
|
|
||||||||||||
|
|
|
|
|
x |
y |
|
|
cos |
cos |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Lx |
Ly |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где 2 = |
2[(n/Lx)2 + (m/Ly)2 + ((2k-1)/2Lz)2]; |
|
|
|
|
|
|
|
|
|
|||||||||||
Knm = 0,5 при n = m = 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Knm = 0,25 при n(m) = 0 и m(n) > 0; |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Knm = 0,125 при n > 0 и m > 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Если q(x,y,t) = const, то последнее выражение существенно упрощается. Например, для практически важного случая q = 1 зависимость (3.49) описывает переходную тепловую характеристику, с помощью которой возможно исследовать температурные поля при различных функциях q(t), применяя метод Дюамеля /112,126/. После подстановки q = 1 и интегрирования выражение (3.49) примет вид
