Учебное пособие 800226

Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

дываем в ряд по формуле (4.10), заменяя в ней

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

1.02 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

	1 1				1	1		1			1	1
f z															.
		2		2			1 z		2				2
			z			5				4		1 z		4
	5 1 z				4

Воспользуемся разложением (4.12),								подставляя вместо z для

первой дроби z2, а для второй z24. Получим ряд Тейлора

	1		1 n			1		1 n
f z		z2n			z2n		1			z2n .
				n 1					n 1
n 0 5			4			5n 0		4

Ближайшими к точке z 0 особыми точками являются точки z 1, поэтому радиус сходимости полученного ряда R 1.

	Пример 9. Разложить в ряд Тейлора по степеням																										z 3,
т.е. в окрестности точки z									3, функцию									f z							1	.
т.е. в окрестности точки z									3, функцию									f z								.
								0														3 2z
																						3 2z
	Решение. Преобразуем данную функцию:
	1						1					1								1					1		.
	3 2z		3 2 z 3 3							3 2 z 3														2			.
	3 2z		3 2 z 3 3							3 2 z 3									3		1			2	z 3
													2								1		3		z 3
																							3
Заменяя в разложении (4.12) z на														z 3 , получим
Заменяя в разложении (4.12) z на														z 3 , получим
												3
1				1			2		22						2		23						3
					1			z 3				z 3							z 3
	3 2z			3	1			z 3				z 3					33		z 3
	3 2z			3	3				32								33

		1			2				22					2		23					3
							z 3				z 3							z 3					.
			3			32	z 3		33		z 3					34		z 3					.

Этот ряд представляет собой бесконечную геометрическую прогрессию со знаменателем q 2 z 3 , поэтому он схо-

		2			3			3
дится при	q		z 3	1 или		z 3			, т.е. радиус сходимо-

		3
							2
							2

сти ряда R 3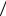2.

Пример 10. Разложить					f z ln 2 z z2	в окрестно-
сти точки z 0 в ряд Тейлора.
Решение. Преобразуем данную функцию:
ln	2 z z2
ln	2 z z2	ln 1 z		2 z ln 1 z ln 2 z
			z				z
ln 1 z ln 2 1					ln 1 z ln2 ln 1			.
ln 1 z ln 2 1			2		ln 1 z ln2 ln 1			.
			2			2

Первое слагаемое раскладываем в ряд по формуле (4.10), второе слагаемое является постоянной, третье слагаемое раскла-

Получаем

ln 2 z z2 ln2 z

2 2

3 2

n 1

ln2 1

ln2

n 1

n 1 n2n

n 1

Ближайшей к точке z 0 особой точкой данной функции является точка z 1, поэтому радиус сходимости полученного ряда R 1.

Пример 11. Найти несколько первых членов разложения

в ряд по степеням	z функции			f z tgz и найти		радиус
сходимости ряда.
Решение. Пусть искомый ряд имеет вид
f z	c c z c z			2 c z3 ,
	0	1	2	3
где коэффициенты c	находим по формуле (4.9) c				f n 0
							.
							.
n				n		n!
						n!

c0 f 0 0 f 0 tg0 0.

Найдем производные f n z . Имеем

z ,

z cos2 z

или f

1 f

(1*)

f z 2f z f z ,

f z

2 f 2 z f

z f z ,

f IV z

2 3f

z f

z f z ,

(2*)

fV z 2

3f 2

z 4f z f z

f z f

IV z

...............................................................................

Полагая в (1*) и (2*) z 0, найдем

f 0 1,

f 0 0 ,

f 0 2,

f IV 0 0,

fV 0 16,

Подставляя найденные значения производных в ряд, получим

tg z z 2 z3 16 z5 3! 5!

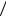Ближайшей к точке z 0 особой точкой данной функции является точка z 2, поэтому радиус сходимости полученного ряда R 2.

4.4. Ряды Лорана

Рядом Лорана называется ряд вида

c n

c 2

c 1

cn z z0 n

z z0

z z

c z z

z z

(4.13)

где z0 – фиксированная точка комплексной плоскости, а cn –

коэффициенты ряда Лорана (заданные комплексные числа). Теорема Лорана. Если функция f z однозначна и ана-

литична в кольце 0 r z z0 R , то в этом кольце она пред-


ставима сходящимся рядом Лорана: f z	cn z z0 n ,
	n

причем это представление единственно; а коэффициенты cn

однозначным образом определяются равенствами


cn	1			f z	dz , r R, n 0, 1, 2, (4.14)
cn				n 1	dz , r R, n 0, 1, 2, (4.14)
	2 i	z z0	z z0
	2 i	z z0	z z0

На практике при нахождении коэффициентов cn стара-

ются избегать применения формул (4.14), так как они приводят к громоздким выкладкам. Обычно, если это возможно, используются готовые разложения в ряд Тейлора элементарных функций.

Если функция	f z аналитична в круге	z z0	R , то
разложение f z в	ряд Лорана в этом круге представляет со-

бой разложение f z в ряд Тейлора – в этом разложении от-

сутствуют слагаемые, содержащие отрицательные степени

z z0 .

Ввыражении (4.13) ряд

c n

c 2

c 1

cn z z0

(4.15)

z z0

z z

называется главной частью ряда Лорана, а ряд

cn z z0 n c0 c1 z z0 cn z z0 n

(4.16)

n 0

называется правильной частью ряда Лорана.

Пример 12. Разложить функцию f z

в ряд

z2 1 2

Лорана в кольце 0 z 1 2.

Решение. Преобразуем данную функцию следующим образом:


f z			1			1			1	1			2

		z2 1 2
		z2 1 2				4		z 1				z 1
1	1			1	1		1		1		1		1	.	(1*)
4 z 1 2				4 z 1			4 z 1				4 z 1 2			.	(1*)
4 z 1 2				4 z 1			4 z 1				4 z 1 2

Первые два слагаемых в правой части (*) имеют нужный вид, так как представляют собой степени разности z 1. Последние два слагаемых запишем в виде

1	1	1 1				1	1		z 1			2
					,			1			.
	z 1 2		z		,			1			.
z 1		21	z	1		z 1 2	4			2
z 1		21		2		z 1 2	4			2
				2

Применяя формулу (4.12), а затем формулу (4.11) при 2, получим

1						1						z 1			z 1 2						z 1 3
								1																		,	(2*)
								1					2									2				,	(2*)
		z 1				2							2				2					2

			1						1					z 1				2	2 1 z 1 2
											1 2
	z 1 2										1 2			2						2!
	z 1 2								4					2						2!						2

							2 2 1 2 2 z 1 3
																								.			(3*)
													3!							2				.			(3*)
													3!							2

Подставляя (2) и (3) в (1*), найдем
			f z									1				1			1				1		1
			f z							z2 1 2						4 z 1 2
										z2 1 2						4 z 1 2							4 z 1
				1					z 1				z 1 2						z 1 3
					1
					1				2						2					2
				8					2						2					2

															84

						1							z 1				3					z 1							2					4			z			1			3
										1
										1									2															3
						16											2		2															3
						16											2																	2
1				1					1			1				3				1														5								2				3								3
																						z 1														z 1													z 1
	4		z 1 2							4	z 1			16						8		z 1										64				z 1										64			z 1
				Пример 13. Разложить функцию																																		f z zcos														z			в ряд
				Пример 13. Разложить функцию																																		f z zcos													z 4				в ряд
Лорана в окрестности точки z0 4.																																																			z 4
Лорана в окрестности точки z0 4.
				Решение. Преобразуем данную функцию:
zcos					z		z 4 4 cos											z 4 4										z 4 4 cos																					1					4
zcos							z 4 4 cos																					z 4 4 cos																					1
					z 4															z 4
					z 4															z 4																																	z 4
						z 4 4										cos1cos										4								sin1sin											4				.						(*)
						z 4 4										cos1cos																		sin1sin															.						(*)
																											z 4																z 4
																											z 4																z 4
Для любого комплексного																							имеем
									2			4			6																												3						5					7
cos 1																		;										sin
cos 1												4!				6!		;										sin																								7!
						2!						4!				6!																								3!						5!						7!
Полагая									4				и подставляя в (*), получим
Полагая								z 4					и подставляя в (*), получим
								z 4
	f z cos1 z 4 4																												4		2													4		4
																													4															4

																					1
																									2! z 4												2				4! z 4									4
																									2! z 4																4! z 4
																	4									4				3												4		5
		sin1 z 4 4															4									4																4
		sin1 z 4 4
															z 4																			3					5! z				4					5
																								3! z 4															5! z				4
					cos1 z 4 4 cos1 sin1																												cos1																16
																																								sin1
																																					2			sin1
																																					2										z 4
											sin1					32										cos1																			128
						cos1																													sin1
						cos1								z 4 2															4						sin1								z 4 3
													3	z 4 2															4												3		z 4 3

Это разложение справедливо для любой точки z 4. В данном случае «кольцо» представляет собой всю комплексную плос-

кость с одной выколотой точкой z 4, поэтому «кольцо» оп-

ределяется следующим образом: 0

z 4

Пример 14. Рассмотреть различные разложения в ряд

Лорана функции

f z

по степеням z (z0 0).

2 z z2

Решение. Разложим знаменатель на линейные множите-

ли и представим

f z в виде суммы двух дробей:

f z

(1*)

1 z 2 z

1 z

2 z

Видно, что функция имеет две особые точки:

z1 1 и

z2 2.

Следовательно, имеются три

«кольца»

с центром

в точке

z0 0, в каждом из которых

f z

аналитическая (рис. 4.1):

I. круг

II. кольцо 1

III. 2

– внешность круга

Найдем ряды Лорана для функции в каждом из этих «колец». I. Используя формулу (4.12), получим

1 z z2

z3 zn ,

(2*)

1 z

n 0

. (3*)

2 z

n 1

4 8

n 0

Условие сходимости ряда (2*)

1 и условие сходимости ря-

1 или

да (3*)

2 выполняются в области I (

1). Под-

ставляя (2*) и(3*) в (1*), получим разложение функции f z в

области I:

1 n

f z

zn .

n 1

n 0

3n 0

n 0

Видим, что получился ряд Тейлора. Это является следствием того, что область I представляет собой круг.

II. В этой области 1 z 2, поэтому условие сходимости

ряда (3*) выполняется, а для ряда (2*) нарушается. Преобразуем первую дробь и разложим ее в ряд следующим образом:

. (4*)

1 z

z 1

n 1

1, т.е. при

Этот ряд сходится для

1. Подставляя (4*) и

f z

(3*) в (1*), получим разложение функции

в области II:

1 n

1 1

1 n

f z 3

2n 1 z

2n z

n 1

n 0

n 1

n 0

Видим, что для кольца ряд Лорана содержит и правильную и главную части.

III. В этой области z 2, поэтому условие сходимости

ряда (4*) выполняется, а для ряда (3*) нарушается. Преобразуем вторую дробь и разложим ее в ряд следующим образом:

1	1		1		2	4		8			1	n 1	2	n 1
				1											. (5*)
z 2				1			2	z	3			zn			. (5*)
z 2		2 z			z z		2	z	3			zn
	z 1									n 1
	z 1	z								n 1
		z

Этот ряд сходится для 2 1, т.е. при z 2. Подставляя (4*) и z

(5*) в (1*), получим разложение функции f z в области III:

1 n 1 2n 1

1 n 1 2n 1 1

f z

n 1 z

n 1

Видим, что для бесконечного кольца ряд Лорана содержит только главную часть.

Этот пример показывает, что для одной и той же функции f z ряд Лорана, вообще говоря, имеет разный вид для раз-

ных областей.

	y		III	y		III
	y

				2
		II		2		II
		II				II
		I
		I		0	3	x
				-2	z0	I
-2	0	1	x	-2	z0	I

Рис. 4.1		Рис. 4.2
Пример 15. Рассмотреть различные разложения в ряд
Лорана функции f z	2z	по степеням z z (z	0	3 2i).

	0
	z2 4

Решение. Разложим знаменатель на линейные множители и представим f z в виде суммы двух дробей:

f z	2z		2z		1		1	.	(1*)
	z2 4	z 2i z 2i			z 2i
							z 2i
Видно, что	функция		имеет две	особые		точки:			z1 2i и

z2 2i. Следовательно, имеются три «кольца» с центром в

точке z0 3 2i, в каждом из которых функция	f z анали-
тична (рис. 4.2):

I. круг

z z0

z 3 2i

3 (радиус первой окружности);

II. кольцо 3

z 3 2i

5 (радиус второй окружности);

III. 5

z 3

– внешность круга

z z0

Найдем ряды Лорана для функции в каждом из этих «колец», используя формулу (4.12).

I. Преобразуем дроби в (1*) и разложим их в ряд:

z 2i

3 4i

z 3 2i 3 4i

z 3 2i

3 4i

z 3 2i

z 3 2i 2

z 3 2i 3

, (2*)

3 4i

z 2i

z 3 2i

3 3

z 3 2i

z 3 2i 2

z 3 2i 3

(3*)

z 3 2i

z 3 4i

1 и

z 3 2i

1 в круге

Так как

3 4i

z 3 2i

3, то ряды (2*) и (3*) сходятся в области I. Подста-

вив (2*) и(3*) в (1*), получим разложение функции

f z

в об-

ласти I:

1 n

f z

n 0

z 3 2i

n 0

3 2i

3 4i

3 4i n

3 4i n 1

z 3 2i .

n 1

n 0

II. В кольце 3

z 3 2i

5 для знаменателей геометри-

ческих прогрессий

получаем

z 3 2i

z 3 4i

1 и

3 4i

z 3 2i 5 1, поэтому ряд (2*) сходится в этой области, а 3 3

ряд (3*) расходится. Преобразуем вторую дробь и разложим ее в ряд следующим образом:

z 2i

z 3 2i 3

z 3 2i 1

z 3 2i

, (4*)

z 3 2i

Так как

то ряд (4*) сходится в области II.

z 3 2i

Подставив

(2*)

и(4*) в

(1*),

получим

разложение

функции

f z в области II:

3 4i

n 1

f z

z 3 2i n

25n 1

n 0

n 0 z 3 2i n 1

III. В этой области 5 z 3 2i , поэтому условие

сходимости ряда (4*) выполняется, а для ряда (2*) нарушается. Преобразуем первую дробь и разложим ее в ряд следующим образом:

1	1	1	1
	z 3 2i 3 4i			3 4i
z 2i		z 3 2i 1

z 3 2i

3 4i

, (5*)

z 3 2i

3 4i

1, то ряд (5*) сходится в об-

Так как

z 3 2i

ласти III.

Подставив (5*) и(4*) в (1*), получим разложение функ-

ции f z

в области III:

1 n

3 4i n

1 n 3n

f z

z 3 2i n 1

n 0

3 4i n 1

3n 1

n 1

z 3 2i n

n 1

4.5. Нули функции

Пусть функция f z

является аналитической в точке z0 .

Точка z0 называется нулем функции f z

порядка (или крат-

ности) n, если выполняются условия:

f z0 0,

, f n 1 z0 0,

f n

z0 0.

Если n 1, то точка z0 называется простым нулем.

Точка z0

тогда и только тогда является нулем n-го по-

рядка функции

f z , аналитической в точке

z0 ,

когда в не-

которой окрестности этой точки имеет место равенство

f z

z z

n z ,

где функция z аналитична в точке z0

и z0 0.

Пример 16. Найти нули функции f z 1 cosz и опре-

делить их порядок.

Решение.	Приравнивая f z нулю,			получим cosz 1,
откуда zn 2n 1		(n 0, 1, 2, ) –		нули данной функ-
ции. Далее находим
	f 2n 1 sin 2n 1 0,

f 2n 1 cos 2n 1 1 0.

Следовательно,	точки	zn 2n 1	(n 0, 1, 2, ) явля-

ются нулями второго порядка данной функции.

Пример 17. Найти нули функции f z 1 ez и опреде-

лить их порядок.

Решение. Приравнивая f z нулю, найдем нули данной функции zn 2n i (n 0, 1, 2, ). Далее находим

f 2n i e2n i 1 0.

Следовательно, точки zn 2n i (n 0, 1, 2, ) – простые нули данной функции.

Пример 18. Найти порядок нуля z0 0 для функции

f z z8 . z sin z

Решение. Используя разложение функции sin z в ряд Тейлора в окрестности точки z0 , получим

f z

z sin z

z z

5 z .

z	– функция, аналитическая		в точке	z0 0, причем
0 6 0. Следовательно, точка			z0 0 является нулем пя-
того порядка данной функции.
Пример 19. Найти нули функции f z z2 1 3 sh z и
определить их порядки.				z2 1 3 sh z 0,
Решение.		Полагая f z 0,	получим
откуда	z2 1 0	или sh z 0. Решая эти уравнения, находим

нули функции	f z :
z i,		z i,	z k i	(k 0, 1, 2, ).
Пусть z i, тогда функцию f z					можно представить в виде
f z z i 3 z , где			функция	z z i 3 sh z является
аналитической	в	точке z i,			причем i 8ishi

8sin1 0. Это означает, что точка z i есть нуль третьего порядка. Аналогично доказывается, что и точка z i является нулем третьего порядка. Исследуем нули z k i (k 0, 1, 2, ). Находим производную

f z 6z z2 1 2 sh z z2 1 3 ch z ,

f k i k i 2 1 3 cosk 0 .

Следовательно, z k i (k 0, 1, 2, ) – простые нули.

4.6. Изолированные особые точки

Если функция f z аналитична в области D, за исклю-

чением некоторых точек, то эти точки называют особыми. Пусть однозначная функция f z аналитична в некото-

рой проколотой окрестности точки z0 (т.е. в некотором

кольце 0 z z0 R), но не аналитична в точке z0 . В этом случае точка z0 называется изолированной особой точкой

функции f z .

Проведем классификацию изолированных особых точек. 1) Изолированная особая точка z0 функции f z назы-

вается устранимой особой точкой, если существует конечный

предел lim f z .

z z0

Изолированная особая точка является устранимой тогда и только тогда, когда главная часть ряда Лорана функции f z в окрестности этой точки тождественно равна нулю.

Пусть функция f z представима в виде	f z	z	и

	z

изолированная особая точка z0 – нуль порядка k для функции

z	и нуль порядка m для функции z . Тогда, если k m ,
то z0	является устранимой особой точкой.

Пример 20. Определить характер особой точки для

функции f z 1 e z . z

Решение. Особая точка функции f z есть z0 0.

Первый способ. Найдем предел, пользуясь следствием из второго замечательного предела

lim	f z lim	1 e z	lim		e z 1	1.
		z
z z0	z 0			z 0	z
Следовательно, точка z0 0		есть устранимая особая точка.
Второй способ. Используя разложение в ряд Тейлора для
функции e z в окрестности точки				z0 0, получим лоранов-

ское разложение функции f z в окрестности нуля

f z 1z 1 e z

1 1 z

Это разложение не содержит главной части, поэтому точка z0 0 является устранимой особой точкой.

Третий способ. Запишем функцию в виде

1 e z			z
f z				.
	z
		z

Точка z0 0 является нулем для функций z и z , так как 0 1 e0 0 и 0 0. Найдем производные

z e z ,	0 1 0,			z 1.
Следовательно, точка	z0 0	является нулем первого порядка
для функций z и z . Таким образом точка z0					0	явля-
ется устранимой особой точкой для функции f z .
Заметим, что функция		f z , доопределенная			в	точке
z 0 единицей, т.е.
	1 e z
			, если	z 0
			, если	z 0
f z		z
			если	z 0
	1,		если	z 0
является аналитической и в точке z 0.
2) Изолированная особая точка				z0 называется полюсом
функции f z , если lim f z .
z z0

Изолированная особая точка является полюсом функции f z тогда и только тогда, когда главная часть ряда Лорана

функции f z в окрестности этой точки содержит конечное

(и отличное от нуля) число ненулевых членов

	c n		c 1
f z	c n		c 1	ck z z0 k	(c n 0).
f z	z z	n	z z0	ck z z0 k	(c n 0).
	z z	n	z z0	k 0
	0

При этом наибольшая степень слагаемых в главной части ряда Лорана (n) будет являться порядком полюса.

Точка

z0 является полюсом

n-го порядка функции

f z

тогда и только тогда, когда функция f z

представи-

ма в виде частного

f z

, где функция z анали-

z z n

тична в точке z0

и z0 0.

f z , то z0

Если точка z0

– полюс порядка n функции

– нуль кратности n функции

f z

Точка

–

полюс

порядка

функции

f z , если

lim z z n

f z C 0.

z z0

Пусть функция f z

представима в виде f z

изолированная особая точка z0 – нуль порядка k

для функции

и нуль порядка m для функции z . Тогда, если k m ,

то z0

является полюсом порядка n m k .

Пример 21. Определить характер особой точки для

функции f z

sin z z

Решение. Особая точка функции f z есть					z0 0. Най-
дем предел lim	1		1	, следовательно,	особая точка

z 0 sin z z		0

z0 0 является полюсом. Используя разложение в ряд Тейлора

sin z z

получим,

что

функция

sin z z

имеет в точке z0

нуль третьего

f z

порядка. Отсюда следует, что функция

f z

имеет в

точке z0 0

полюс третьего порядка.

sin z z

Пример 22.

Определить характер особой точки для

функции

f z

sin z

z3 z2 z 1

Решение.

Разложим

знаменатель

на

множители:

z3 z2 z 1 z 1 2 z 1 .

Отсюда получаем,

что функция

f z имеет две особые точки z1 1 и z2 1.

Для исследования характера точки z1 1 представим функцию в виде

sin z

1 z

f z

z 1

z 1 2 z 1

z 1 2

где 1 z аналитична

в окрестности точки z1 1, причем

sin 1

sin1

0 . Следовательно, точка z

1 явля-

1 1

ется полюсом второго порядка данной функции. Аналогично, для исследования точки z2 1, запишем

sin z

			f z	sin z	z 1 2			2 z		,
				z 1 2 z 1
					z 1			z 1
где 2 z аналитична в окрестности						точки			z2 1, причем
2	1	sin1	0. Следовательно,		точка		z2 1		является про-

	4

стым полюсом данной функции.

Пример 23. Определить характер особой точки для

функции f z	sin2 z	.

	2ez 1 z2 1

Решение. Замечаем, что z0 1 является особой точкой функции f z , так как при этом значении знаменатель функ-

ции обращается в нуль. Представим данную функцию в виде


	sin	2 z		z
					. Найдем порядок нуля для функций z
	2ez 1				. Найдем порядок нуля для функций z
	2ez 1	z2 1	z
и z . Имеем:
					1 sin2 0;
	z 2 sin zcos z sin(2 z) ,					1 sin 2 0;

z 2 2 cos 2 z , 1 2 2 cos 2 2 2 0;

1 2e0 1 1 0;

z 2ez 1 2z , 1 2e0 2 0;

z 2ez 1 2, 1 2e0 2 0 ;

z	2ez 1, 1 2e0	2 0.
Таким образом, z0 1	является нулем второго порядка (k 2)
для функции z и нулем третьего		порядка (m 3) для

функции z . Следовательно, для данной функции точка

z0 1 есть полюс первого порядка, так как n m k 3 2 1.

Пример 24. Определить характер особой точки для функ-

1 cosz

ции f z . z7

Решение. Очевидно, что z0 0 является особой точкой функции f z . Раскладывая функцию cosz в ряд Тейлора по

степеням z , получим лорановское разложение функции

f z

в окрестности нуля:

z10

1 1

1 cosz

10!

f z

z10

10!

2!z5

4!z3

6!z 8!

10!

Это разложение содержит конечное число членов с отрицательными степенями z . Следовательно, точка z0 0 является

полюсом пятого порядка, так как наибольший показатель степени у z , содержащихся в знаменателях членов главной части ряда Лорана, равен пяти.

3) Изолированная особая точка	z0 называется сущест-
венно особой точкой функции f z ,	если lim f z не суще-

z z0

ствует.

Изолированная особая точка является существенно особой точкой функции f z тогда и только тогда, когда глав-

ная часть ряда Лорана функции f z в окрестности этой точки содержит бесконечное число ненулевых членов.

<<< < Предыдущая 1 2 3 45 / 75 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2022991.69 Кб2Учебное пособие 800221.pdf
#
01.05.2022993.74 Кб5Учебное пособие 800222.pdf
#
01.05.20221 Mб1Учебное пособие 800223.pdf
#
01.05.20221.01 Mб4Учебное пособие 800224.pdf
#
01.05.20221.02 Mб3Учебное пособие 800225.pdf
#
01.05.20221.02 Mб2Учебное пособие 800226.pdf
#
01.05.20221.03 Mб1Учебное пособие 800227.pdf
#
01.05.20221.03 Mб1Учебное пособие 800228.pdf
#
01.05.20221.03 Mб1Учебное пособие 800229.pdf
#
01.05.2022289.9 Кб1Учебное пособие 80023.pdf
#
01.05.20221.04 Mб4Учебное пособие 800230.pdf