
Учебное пособие 800226
.pdf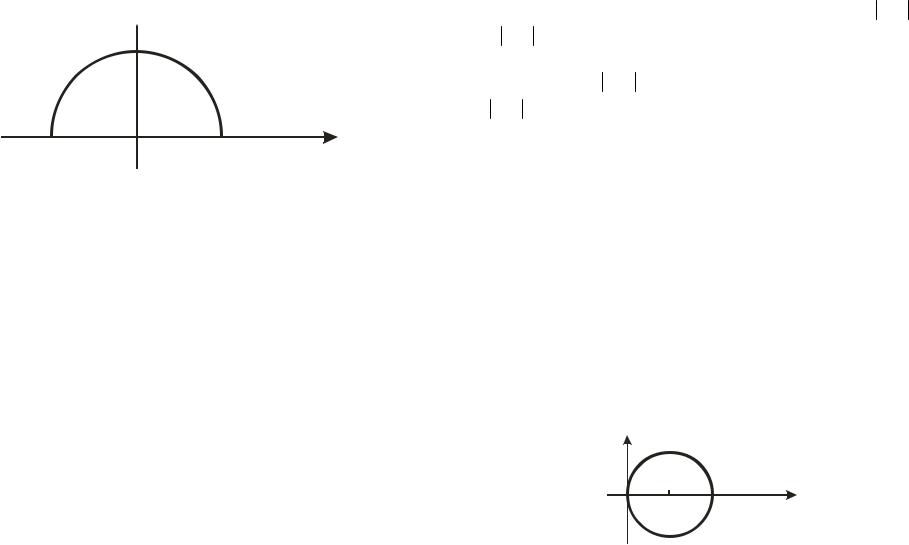
y
1
-1 |
1 |
x |
|
Рис. 1.4 |
|
Кривая называется гладкой, если ее уравнение можно за- |
||
писать в виде |
z (t), t , где функция (t) |
имеет на |
отрезке , |
непрерывную и отличную от нуля производную |
|
|
|
|
|
(t) 0, причем, если кривая замкнута, то должно выполнять- |
|||
|
|
|
|
ся равенство ( ) ( ). |
|
|
|
Кривая называется кусочно гладкой, если ее можно раз- |
|||
бить на конечное число гладких кривых. |
|
||
Пусть на луче t |
задана непрерывная |
комплексно- |
|
значная функция |
z (t) и ( ) , т.е. lim |
(t) . То- |
|
|
|
t |
|
гда говорят, что задана неограниченная кривая |
|
||
|
z (t), |
t , |
(1.35) |
а уравнение (1.35) называется параметрическим уравнением
этой кривой. Неограниченная кривая (1.35) называется кусочно гладкой, если для каждого конечного кривая z (t),t является кусочно гладкой.
Аналогично определяются неограниченные кривые в случае, когда параметр t пробегает полуось t или всю числовую ось.
20
Пример 1.15. Какая кривая задается уравнением z c
z c 2a, где c и a – действительные положительные чис-
ла, причем a c ? |
|
Решение. z c |
– расстояние между точками z и c, |
z c – расстояние между точками z и c. По условию сумма
расстояний от точки z до двух данных точек z1 c и z2 c есть величина постоянная. Значит, точка z лежит на эллипсе.
Уравнение этого эллипса |
имеет вид |
x2 |
|
y2 |
1, |
где |
||||||||||||||||||||
a2 |
b2 |
|||||||||||||||||||||||||
b2 a2 |
c2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Пример 1.16. Какая кривая определяется уравнением |
|||||||||||||||||||||||
Re |
1 |
|
|
1 |
? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
||||
|
|
|
Решение. |
Так |
как z x iy, |
то |
Re |
Re |
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
x iy |
||||
Re |
|
|
x iy |
|
Re |
|
x iy |
|
|
x |
|
|
1 |
. |
Следовательно, |
|||||||||||
|
|
|
|
|
x2 y2 |
x |
2 y2 |
|
||||||||||||||||||
|
|
|
(x iy)(x iy) |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||
x2 y2 |
4x 0. Это окружность x 2 2 |
y2 |
4 (рис. 1.5). |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||
Рис. 1.5
Множество D точек расширенной комплексной плоскости называется областью, если это множество
21

открытое, т.е. для каждой точки, принадлежащей D, существует окрестность этой точки, принадлежащая D;
связное, т.е. любые две точки, принадлежащие D, можно соединить кривой, быть может, неограниченной, все точки которой принадлежат D.
Граничной точкой области D называется точка, в любой окрестности которой есть точки, принадлежащие D, и точки, не принадлежащие D. Множество граничных точек области называется границей этой области. Область D, дополненная всеми своими граничными точками, называется замыканием области D и обозначается D.
Всюду в дальнейшем будем рассматривать только такие области, границы которых состоят из конечного числа кусочно гладких кривых и изолированных точек. Кроме того, будем считать, что все граничные кривые области D ориентированы так, что при движении точки вдоль граничной кривой в направлении этой ориентации область D остается слева.
Пример 1.17. Границей области 0 z 2 1 является точка z 2 и окружность z 2 1, ориентированная против
часовой стрелки и проходимая один раз (рис. 1.6). Эту область
будем называть так: круг |
z 2 |
1 |
с выколотой точкой z 2. |
Граница на рисунке изображена штриховой линией, так как она не входит в область.
y |
|
|
|
1 |
2 |
3 |
x |
Рис. 1.6
22
Пример 1.18. Какое множество точек на комплексной
плоскости определяется условием arg z 1 i 3 ? 2 4
Решение. Комплексное число z 1 i z ( 1 i) изображается вектором, началом которого является точка 1 i, а концом – точка z . Угол между этим вектором и осью Ox есть
arg z 1 i |
и он меняется от |
|
до |
3 |
. Следовательно, |
|
2 |
4 |
|
||
данное неравенство определяет угол между лучами, выходя-
щими из точки 1 i и образующими с осью Ox |
углы |
|
и |
||
|
|||||
|
3 |
|
2 |
|
|
|
(рис. 1.7). |
|
|
|
|
4 |
|
|
|
||
|
|
|
|
||
y
1
-1 x
Рис. 1.7
Пример 1.19. Какое множество точек на плоскости комплексного переменного определяется условиями 1 z i 2,
argz . 4 2
23

Решение. Первое двойное неравенство определяет внутренность кольца с центром в точке z i и радиусами 1 и 2. Второе двойное неравенство определяет область межу лучами, выходящими из точки z 0 и образующими с осью Ox углы
|
|
и |
|
. Следовательно, искомое множество точек является |
|
|
|||
4 |
2 |
|
||
сектором кольца (рис. 1.8). Так как заданы строгие неравенства, то граница не входит в область, и поэтому она изображена штриховой линией.
y
1
x
-1
Рис. 1.8
y
2
1
x
Рис. 1.9
Пример 1.20. Условие 1 Im z 2 определяет полосу 1 y 2 на комплексной плоскости (рис. 1.9).
Область D называется ограниченной, если существует такой круг K : z , что D K . Примерами ограниченных
областей являются области на рис. 1.6 и 1.8. Области на рис. 1.7 и 1.9 являются неограниченными.
Область D на комплексной плоскости называется односвязной, если любую замкнутую кривую, лежащую в D, можно непрерывно деформировать в точку, оставаясь в области D. Образно односвязную область можно представить как лист бумаги произвольной формы, может быть, с разрезами по краям, но без «дырок» внутри. Примерами односвязных областей являются области на рис. 1.7, 1.8, 1.9. Область на рис. 1.6 является неодносвязной.
Определение односвязной области на расширенной комплексной плоскости такое же, как и на нерасширенной комплексной плоскости, только непрерывную деформацию кривой в точку z нужно рассматривать на сфере Римана.
Пример 1.21. Следующие области расширенной комплексной плоскости являются односвязными:
а) z 1;
б) вся расширенная комплексная плоскость;
в) z a – вся расширенная комплексная плоскость с выколотой точкой a.
Пример 1.22. Следующие области расширенной комплексной плоскости являются неодносвязными:
а) z 1, z i – вся расширенная комплексная плоскость с выколотыми точками 1 и i;
б) вся расширенная комплексная плоскость с разрезами по отрезкам 0, 1 и i, 2i ;
в) 1 z .
24 |
25 |

ГЛАВА 2 ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
И ИХ ДИФФЕРЕНЦИРОВАНИЕ
2.1. Основные понятия о функции комплексного переменного
Если каждому комплексному числу z D поставлено в соответствие некоторое комплексное число w, то говорят, что в области D определена функция w f z . Геометрически
заданную на D функцию w f z можно рассматривать как
отображение области D плоскости z на некоторое множест-
во G плоскости w , являющееся совокупностью значений
f z , соответствующим всем z D.
Один из наиболее употребляемых способов задания функции – задание с помощью формулы – в случае функций комплексной переменной часто приводит к многозначным функциям. Говорят, что в области D определена многозначная функция w f z , если каждой точке z D поставлено в со-
ответствие несколько комплексных чисел w.
Функция w f z называется однолистной в области
D, если любым различным значениям z1 z2, взятым из об-
ласти D, соответствуют различные значения f z1 |
f z2 . |
Пусть z x iy и w u iv. Тогда функция |
w f z |
может быть представлена с помощью двух действительных
функций |
u u x, |
y |
и |
v v x, y действительных перемен- |
ных x |
и y : |
|
w |
f z u iv u x, y iv x, y , где |
u x, y Re f z , v x, y Im f z .
Пример 1. Найти действительную и мнимую части функ-
ции f z iz2 z .
Решение. Полагая z x iy, находим
f z u x, y iv x, y i x iy 2 x iy
i x2 2ixy y2 x iy x 2xy i x2 y2 y .
Таким образом
Re f z u x, y x 2xy , Im f z v x, y x2 y2 y .
Пример 2. Определить функцию w f z по известным
действительной |
и мнимой частям: u x, y x2 |
y2 2y 1, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
v x, y 2xy 2x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. Так как z x iy |
и |
z |
|
x iy, то x |
1 |
z |
z |
и |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
y |
z |
z |
. |
Тогда u x, y x2 y2 2y 1 |
1 |
|
z |
z |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
2 i z |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
1 |
|
z |
z |
2 i z |
z |
1 |
1 |
z |
z |
1; |
|
|
|
|
|
|
|
v x, y |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2xy 2x |
i |
z2 |
z |
2 z |
z |
. |
|
Следовательно, |
|
|
|
w u iv |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
1 |
z2 |
z |
|
2 i z |
z |
1 |
1 |
|
|
z2 |
z |
2 i z |
z |
z2 2iz 1. |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
Пример 3. В какую кривую отображается единичная ок- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ружность |
|
z |
|
1 с помощью функции w z2? |
|
|
|
|
|
|
|
2 1. По- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. Так как по условию |
|
z |
|
1, то |
|
w |
|
|
|
z |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
этому образом окружности |
|
z |
|
1 |
в плоскости z |
является ок- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ружность |
|
w |
|
1 |
в плоскости w , проходимая дважды. Это |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
следует из того, |
что поскольку w z2, то Argw 2Argz 2k , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
26 |
27 |

так что когда точка z |
описывает полную окружность |
|
z |
1, то |
|||||||||||||
ее образ описывает окружность |
|
w |
|
1 дважды. |
|
|
|
||||||||||
|
|
|
|
|
|||||||||||||
Пример |
4. |
Найти |
область |
|
однолистности |
функции |
|||||||||||
w z2. |
|
|
z rei 1 |
|
|
|
|
|
|
|
r ei 2 |
|
|
|
|
||
Решение. Пусть |
|
|
и z |
2 |
. Найдем условие, |
||||||||||||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
при котором z2 |
z2, |
хотя z |
z |
2 |
. Имеем r2e2i 1 r2e2i 2 . От- |
||||||||||||
1 |
|
2 |
|
1 |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
сюда заключаем, |
что |
r1 r2, |
а |
|
2 2 |
2 1 2k (k 0,1). Так |
|||||||||||
как z1 z2, то 2 |
1 . Таким образом, |
область однолист- |
|||||||||||||||
ности функции w z2 не должна содержать внутри себя точек, модули которых совпадают, а аргументы отличаются на , т.е. областью однолистности является любая полуплоскость, например Rez 0 или Im z 0.
Пример 5. Найти отображение, осуществляемое линейной функцией w az b .
Решение. Это отображение можно рассматривать как композицию трех простейших отображений. Действительно,
положим w |
|
a |
|
z , w |
w eiarga |
, w w b. Нетрудно видеть, |
|
|
|
||||||
1 |
|
|
|
2 |
1 |
3 |
2 |
что w w1 w2 w3. Из геометрического смысла произведения и суммы комплексных чисел ясно, что отображение w1 есть отображение растяжения (сжатия при 0 a 1), отображение
w2 представляет собой поворот всей плоскости w1 относи-
тельно начала координат на угол arga и отображение w3
есть параллельный перенос плоскости w2 на вектор, |
изобра- |
||||
жающий комплексное число b . |
|
|
|
||
Пример 6. Найти все значения функции w |
|
|
|
|
|
2 |
|
|
в |
||
|
z |
||||
|
|
||||
2 |
|
|
|
||
точке z0 i. |
|
|
|
||
Решение. Данная функция является многозначной (имеет
два значения). Так как |
|
i |
|
1 и |
argi |
|
, то в соответствии с |
|
|
||||||
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
определением корня из комплексного числа (1.30) находим
|
|
|
|
|
|
i |
2 2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
|
|
(k 0,1). Таким образом, |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
w |
|
|
|
|
e |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
w |
|
|
|
|
|
e 4 |
|
|
|
|
|
cos |
|
|
isin |
|
|
i |
|
|
|
, |
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
2 |
4 |
4 |
|
2 |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
5 |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
w |
|
|
|
|
|
|
e |
|
4 |
|
|
cos |
|
isin |
|
2 i |
. |
|||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
4 |
|
4 |
|
2 |
||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Основные элементарные функции комплексного переменного
Следующие функции (как однозначные, так и многозначные) называются основными элементарными.
1. Дробно-рациональная функция
|
f z |
a zn |
a zn 1 |
a |
n |
|
|
|
|
|||||||||
|
|
0 |
1 |
|
|
|
|
|
|
, |
n, m N . |
|||||||
b zm |
b zm 1 |
b |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
0 |
1 |
|
|
|
|
|
m |
|
|
|
|
|
||
Частными случаями этой функции являются: |
|
|||||||||||||||||
а) линейная функция |
az b, |
a, |
b C, |
a 0; |
||||||||||||||
б) степенная функция |
zn , |
n N; |
|
|
||||||||||||||
в) многочлен |
a zn a zn 1 |
a |
n |
; |
|
|||||||||||||
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
г) дробно-линейная функция |
|
|
|
|
|
|
|
|
|
|||||||||
|
az b |
, |
a, b, c, d C, c 0, |
|
ad bc 0; |
|||||||||||||
|
|
|
||||||||||||||||
|
cz d |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
д) функция Жуковского |
|
|
z |
|
|
|
. |
|
|
|||||||||
2 |
z |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
28 |
29 |

2. Показательная функция ez определяется как сумма абсолютно сходящегося во всей комплексной плоскости сте-
пенного ряда ez 1 z z2 z3 zn . 2! 3! n!
Показательная функция ez обладает следующими свойствами:
а) |
ez1 z2 ez1 ez2 |
, где z |
и z |
2 |
– любые комплексные числа; |
|
ez 2k i ez |
1 |
|
ez является периодической |
|
б) |
(k Z), |
т.е. |
|||
функцией с периодом 2 i ;
в) функция ez непрерывна на всей комплексной плоскости; г) для любого комплексного z x iy имеют место равенст-
ва |
ez |
ex , |
argez y ; |
д) функция ez принимает все значения, кроме нуля, т.е.
уравнение ez A разрешимо для любого комплексного числа
A 0.
3. Тригонометрические функции sin z и cosz определя-
ются степенными рядами:
sin z z |
z3 |
|
z5 |
1 n |
|
z2n 1 |
|
, |
|||||
|
|
|
|
|
|
|
|
||||||
3! |
|
5! |
|
|
2n 1 ! |
||||||||
cosz 1 |
z2 |
|
z4 |
1 n |
z2n |
|
, |
||||||
|
|
2n ! |
|||||||||||
2! |
4! |
|
|
|
|
||||||||
абсолютно сходящимися при всех значениях z .
Для функций ez , sin z и cosz имеют место формулы Эй-
лера: eiz cosz isin z и e iz cosz isin z. Откуда следует:
cosz eiz e iz и sin z eiz e iz . (2.1)
2 2i
Функции sin z и cosz обладают следующими свойства-
ми:
30
а) функции sin z |
и cosz |
непрерывны на всей комплексной |
|
плоскости; |
|
и cosz |
|
б) функции sin z |
принимают все значения, т.е. урав- |
||
нения sin z A |
cosz A |
имеют решения для любого ком- |
|
плексного числа A; |
и cosz |
|
|
в) функции sin z |
– периодические с действительным |
||
периодом 2 и имеют только действительные нули |
z k и |
|||
z |
|
k |
соответственно, где k Z; |
|
|
|
|||
2 |
|
– нечетная функция, cosz – четная функция; |
||
г) sin z |
||||
д) для тригонометрических функций остаются в силе все
формулы тригонометрии: |
|
|
|
|
|
|
|
|
|
||||||||
sin2 z cos2 z 1, |
cos2 z sin2 z cos2z |
sin2z 2sin zcosz, |
|||||||||||||||
|
|
|
sin z1 z2 sin z1 cosz2 |
cosz1sin z2 , |
|
|
|||||||||||
|
|
|
cos z1 z2 cosz1cosz2 |
sin z1sin z2 ; |
(2.2) |
||||||||||||
е) имеют место формулы |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
sin(x iy) sin xch y icosxsh y , |
|
|
|
|||||||||||
|
|
|
cos(x iy) cosxch y isin xsh y . |
|
(2.3) |
||||||||||||
Функции |
tgz и ctgz |
|
определяются |
равенствами: |
|||||||||||||
tg z |
sin z |
и ctgz |
cosz |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
cosz |
|
|
sin z |
|
|
|
|
|
|
|
|
|
||||
4. Гиперболические функции определяются равенствами: |
|||||||||||||||||
shz |
ez e z |
, |
ch z |
ez e z |
|
, th z |
sh z |
|
, |
cth z |
ch z |
. |
|||||
|
|
|
|
ch z |
sh z |
||||||||||||
2 |
|
2 |
|
|
|
|
|
|
|||||||||
Тригонометрические и гиперболические функции связа- |
|||||||||||||||||
ны между собой следующими соотношениями: |
|
|
|
||||||||||||||
|
|
|
|
sin z ishiz , |
sh z isiniz , |
|
|
|
|||||||||
|
|
|
|
|
cosz chiz, |
ch z cosiz, |
|
|
|
|
|||||||
|
|
|
|
tg z ithiz , |
th z itgiz , |
|
|
|
|
||||||||
|
|
|
|
ctgz icthiz, |
cth z ictgiz. |
|
|
(2.4) |
|||||||||
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
||||

Таким образом, свойства функций sh z и ch z непосредственно вытекают из свойств функций sin z и cosz . Отметим, в частности, что функции sh z и ch z непрерывны на всей комплексной плоскости. Имеют место формулы
ch2z sh2z 1, |
ch2z sh2z ch2z, |
2sh zch z sh2z , |
||||||||||
sh z1 z2 sh z1ch z2 ch z1sh z2 , |
|
|||||||||||
ch z1 z2 ch z1 ch z2 |
sh z1sh z2 . |
(2.5) |
||||||||||
5. Логарифмическая функция |
Ln z |
( z 0 ) |
определяется |
|||||||||
как функция, обратная показательной ez , причем |
|
|||||||||||
Ln z ln |
|
z |
|
iArg z ln |
|
z |
|
i argz 2k , |
k Z. |
|||
|
|
|
|
|||||||||
Эта функция является многозначной. Главным значением называется то, которое получается при k 0; оно равно ln z ln z iarg z . Очевидно, что Ln z ln z 2k i . Для лога-
рифмической функции справедливы следующие соотношения:
Ln z z |
2 |
Ln z Ln z |
2 |
, Ln |
z1 |
Ln z Ln z |
2 |
. |
||
|
||||||||||
1 |
|
1 |
|
|
z2 |
1 |
|
|||
|
|
|
|
|
|
|
|
|
Arcsinz, |
|
6. Обратные |
тригонометрические функции |
|
||||||||
Arccosz , Arctgz, Arcctgz |
определяются как функции, обрат- |
|||||||||
ные соответственно к функциям sinw, |
cosw, tgw, ctgw. На- |
|||||||||
пример, если z sin w, то w называется арксинусом числа z и обозначается w Arcsin z. Все эти функции являются многозначными и выражаются через логарифмические функции:
Arcsin z iLn iz |
|
|
1 z2 |
, |
Arccosz iLn z |
z2 1 |
, |
||||||||
Arctgz |
i |
Ln |
1 |
iz |
, |
Arcctgz |
i |
Ln |
z i |
. |
(2.6) |
||||
|
|
|
|
|
|||||||||||
2 |
|
1 |
iz |
2 |
|
z i |
|
|
|||||||
Главные значения обратных тригонометрических функ- |
|||||||||||||||
ций arcsin z , arccosz, |
|
arctgz , |
arcctgz получаются, если брать |
||||||||||||
главные значения соответствующих логарифмических функций.
32
7. |
Обратные гиперболические функции Arsh z , Arch z, |
Arth z, |
Arcth z определяются как функции, обратные соответ- |
ственно к функциям shw, chw, thw, cthw. Например, если |
|
z shw, то w называется ареа-синусом числа z и обозначает- |
|
ся w Arsh z . Все эти функции являются многозначными и выражаются через логарифмические функции:
Arsh z Ln z |
|
z2 1 |
, |
Arch z Ln z |
z2 |
1 |
, |
||||||||||
Arth z |
1 |
Ln |
1 |
z |
, |
|
Arcth z |
1 |
Ln |
z 1 |
. |
(2.7) |
|||||
|
|
|
|
|
|
||||||||||||
2 |
|
1 |
z |
|
|
2 z 1 |
|
|
|||||||||
Главные значения обратных гиперболических функций |
|||||||||||||||||
arshz, arch z , arth z , |
arcth z |
получаются, если брать главные |
|||||||||||||||
значения соответствующих логарифмических функций. |
|||||||||||||||||
8. Общая степенная функция w za , где a i – лю- |
|||||||||||||||||
бое комплексное число, определяется равенством |
za eaLnz . |
||||||||||||||||
Эта функция многозначная, |
ее главное значение равно ealnz . |
||||||||||||||||
Если a 1 (n N), то получаем многозначную функцию – ко- n
рень n-й степени из комплексного числа:
1 |
ln |
|
z |
|
i argz 2k |
|
|
|
i |
argz 2k |
|
|||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
z1 n n z en |
||||||||||||||||
|
|
|
|
|
n |
ze |
n . |
|||||||||
9. Общая показательная функция w az |
(a 0 – любое |
|||||||||||||||
комплексное число) |
определяется |
равенством az ezLna . |
||||||||||||||
Главное значение этой многозначной функции равно ezlna .
Пример 7. Вычислить w sin z при z0 iln(2 
 5) . Решение. Согласно формулам (2.3) получаем
5) . Решение. Согласно формулам (2.3) получаем
w0 sin z0 sin chln(2 
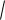 5) icos shln(2
5) icos shln(2 
 5)
5)
ishln(2 
 5) i 1(eln(2
5) i 1(eln(2 
 5) e ln(2
5) e ln(2 
 5))
5))
2
33

|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
i 8 4 5 |
|
|
|
|
|
4 2 5 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
2i . |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
2 5 |
2 2 5 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 5 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
Пример 8. Вычислить ii . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
Решение: Согласно определению общей показательной |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
i |
|
|
iLni |
|
|
|
|
|
|
i ln |
|
i |
|
i argi 2k |
|
|
|
|
|
|
|
|
|
2 2k |
|
|
|
|
|
|
|
|
|
1 |
2 2k |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
функции |
i |
|
e |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||
|
|
|
Пример 9. Записать в алгебраической форме Arctg(1 i). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение. Согласно формуле |
Arctgz |
|
i |
|
Ln |
1 iz |
|
|
полу- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 i 1 i |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 iz |
|
|
|
|
|
|||||||||||||||||||||||
чаем |
Arctg 1 i |
i |
|
Ln |
|
|
i |
|
Ln |
|
|
i |
|
|
i |
|
Ln |
1 2i |
. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 i 1 i |
|
2 |
|
|
|
2 i |
|
2 |
|
|
|
|
|
|
5 |
|
|
|
||||||||||||||||||||||||||||||||||||||
По |
формуле |
Ln z ln |
|
z |
|
|
iArgz ln |
|
z |
|
iargz 2k i |
|
(k Z) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
ln5 i arctg2 2k i. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
имеем Ln |
|
|
|
|
|
|
i |
|
|
|
|
|
Оконча- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
5 |
5 |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
тельно получаем Arctg 1 i |
1 |
arctg2 2k 1 |
|
|
i |
ln5. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
Пример 10. Решить уравнение sin z 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Решение. Задача сводится к нахождению величины |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z Arcsin3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
По формуле (2.6) |
|
получаем |
|
|
|
|
|
z Arcsin3 iLn(3i |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
8) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
iLni 3 |
|
8 i |
|
|
|
|
|
|
|
|
|
|
8 iarg 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
ln 3 |
|
8 2k i |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2k iln |
3 |
|
|
|
|
, где k Z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.2. Предел последовательности комплексных чисел. Предел и непрерывность функции комплексного переменного
Пусть дана последовательность zn комплексных чисел:
z1, z2, , zn,
Определение 1. Комплексное число a называется пределом последовательности zn , если для любого положитель-
ного числа можно указать такой номер N N , начиная с которого все элементы zn этой последовательности удовле-
творяют неравенству zn a при n N . Последова-
тельность zn , имеющая предел a, называется сходящейся к
числу a, что записывается в виде lim zn a.
n
Каждой последовательности комплексных чисел zn
соответствуют две последовательности действительных чисел
xn и yn , где zn xn iyn , n 1, 2,
Теорема 1. Последовательность zn xn iyn сходится
к числу |
a i тогда и только тогда, когда lim |
x и |
|
|
|
n |
n |
lim y |
n |
. |
|
n |
|
|
|
Определение 2. Последовательность zn называется ог-
раниченной, если существует положительное число M такое, что для всех элементов zn этой последовательности выполня-
ется неравенство zn M .
Теорема 2. Всякая сходящаяся последовательность ограничена.
34 |
35 |

Свойства сходящихся последовательностей комплексных чисел
|
|
|
|
|
Если |
|
lim zn a |
и |
lim n b, то |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1. |
lim(zn n) a b; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2. |
lim(z |
n |
) ab; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
3. |
lim |
|
zn |
|
|
a |
|
( n 0, |
b 0 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
n n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Достаточное условие сходимости последовательно- |
||||||||||||||||||||||||||||
сти |
|
комплексных |
чисел. |
Пусть |
z |
n |
r ei n , где |
r |
|
z |
n |
|
, |
||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|||
|
n |
|
argz |
n |
. |
|
|
Тогда, |
если |
lim r |
r |
и lim |
n |
|
0 |
, |
|
|
то |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n n |
|
0 |
n |
|
|
|
|
|
|
|
|
||||
|
lim z |
n |
r ei 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
n |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Если для сколь угодно большого числа M 0 существу- |
||||||||||||||||||||||||||||
ет натуральное число N такое, что все члены zn |
|
последова- |
|||||||||||||||||||||||||||||||
тельности |
|
с |
номерами |
n N удовлетворяют |
неравенству |
||||||||||||||||||||||||||||
|
zn |
|
M , то говорят, |
что последовательность zn |
|
сходится к |
|||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
бесконечно удаленной точке или, просто, к бесконечности, и
пишут lim zn .
n
Дополняя плоскость комплексного переменного так введенной бесконечно удаленной точкой z , получаем расширенную плоскость комплексного переменного.
Окрестностью бесконечно удаленной точки называется совокупность всех точек z , удовлетворяющих неравенству z R (с присоединением бесконечно удаленной точки), т.е.
совокупность всех точек z , лежащих вне круга с центром в начале координат достаточно большого радиуса R .
Определение 3. Окрестностью точки z0 плоскости ком-
плексного переменного z называется всякая область, содер36
жащая эту точку; -окрестностью точки z0 называется мно-
жество всех точек z , лежащих внутри круга радиуса с центром в точке z0 , т.е. множество всех точек z , удовлетворяю-
щих неравенству z z0 .
Пусть функция f z определена в некоторой окрестно-
сти точки z0 , кроме, быть может, самой точки z0 .
Определение 4. Число A называется пределом функции |
|
f z в точке |
z0 , если для любого числа 0 можно указать |
такое число |
0, что для всех точек z , удовлетво- |
ряющих условию |
0 |
z z0 |
, |
выполняется неравенство |
|||
|
f z A |
|
. В этом случае пишут |
lim f z A. Здесь пред- |
|||
|
|
||||||
|
|
|
|
|
|
|
z z0 |
полагается, что z0 |
|
|
|
||||
и A – конечные точки комплексной плос- |
|||||||
кости. |
|
|
|
|
|||
|
Приведем еще одно определение предела функции в точ- |
||||||
ке. Пусть функция |
f z определена в некоторой окрестности |
||||||
точки z0 , кроме, быть может, самой точки z0 . |
|||||||
|
Определение |
5. Если для любой последовательности |
|||||
zn , zn z0 , сходящейся к точке z0 , соответствующая ей по-
следовательность значений функции |
f zn сходится к од- |
ному и тому же комплексному числу A, то число A называют |
|
пределом функции f z в точке z : |
lim f z A. Здесь ко- |
0 |
z z |
|
0 |
нечность z0 и A не предполагается.
Существование предела lim f z , где
z z0 |
|
f z u x, y iv x, y , |
z0 x0 iy0 , |
37

равносильно |
|
существованию |
двух |
пределов |
lim u x, y |
и |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
причем lim f z |
|
|
|
|
|
|
y y0 |
|
|
|
|
|||||||
lim v x, y , |
|
lim u x, y i |
lim v x, y . |
|
|||||||||||||||||
x x0 |
|
|
z z0 |
|
|
|
|
x x0 |
|
|
|
|
x x0 |
|
|
|
|
||||
y y0 |
|
|
|
|
|
|
|
|
y y0 |
|
|
|
|
y y0 |
|
|
|
|
|||
Пределы функций комплексного переменного обладают |
|||||||||||||||||||||
следующими свойствами. Пусть существуют пределы |
|
|
|
|
|||||||||||||||||
|
|
|
|
lim f z A |
и |
|
lim g z B . |
|
|
|
|
|
|||||||||
Тогда |
|
z z0 |
|
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
|
||||
|
|
lim f z g z A B, |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
z z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f z |
g |
z AB, |
|
|
|
|
|
|||||||||
|
|
|
|
|
z z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f z |
|
|
A |
, |
B 0. |
|
|
|
|
|
|||||
|
|
|
|
|
g z |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
z z0 |
|
B |
|
|
|
|
|
|
|
|
|
|||||
Определение 6. Функция |
f z , заданная в области |
D, |
|||||||||||||||||||
называется непрерывной в точке z0 D , если |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
lim |
f z f z0 . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
z z0 |
f z |
|
|
|
|
|
|
|
|
|
|
|
||||
Иными словами: функция |
|
непрерывна в точке |
z0 D , |
||||||||||||||||||
если для любого |
числа |
0 |
|
можно |
указать такое |
число |
|||||||||||||||
0, что |
для всех точек z D, |
удовлетворяющих ус- |
|||||||||||||||||||
ловию |
|
z z0 |
|
, |
выполняется неравенство |
|
f z f z0 |
|
. |
||||||||||||
|
|
|
|
||||||||||||||||||
|
|
||||||||||||||||||||
Для непрерывности функции комплексного переменного |
|||||||||||||||||||||
f z u x, y iv x, y |
в точке z0 x0 iy0 необходимо и дос- |
||||||||||||||||||||
таточно, чтобы ее действительная и мнимая части, т.е. функ-
ции u x, y и v x, y , были непрерывны в точке |
x0, y0 по |
совокупности переменных x и y . |
|
Определение 7. Функция f z комплексного переменно-
го называется непрерывной в области D, если она непрерывна в каждой точке этой области.
Определение 8. Сумма, разность и произведение двух
функций комплексного переменного f z и g z , непрерыв- |
|||
ных в области D, также являются непрерывными функциями в |
|||
этой области, а функция |
f z |
непрерывна в тех точках облас- |
|
|
|||
|
g z |
|
|
ти D, где g z 0. |
|
|
|
Определение 9. Если функция f z |
непрерывна в точке |
||
z0 , а функция F непрерывна в точке |
0 f z0 , то слож- |
||
ная функция F f z |
непрерывна в точке z . |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
f z |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Определение 10. Функция |
|
комплексного перемен- |
||||||||||||||||||||
ного называется равномерно непрерывной в области |
D, если |
|||||||||||||||||||||||
для |
любого |
|
числа |
0 можно |
указать |
такое |
|
число |
||||||||||||||||
0, |
что для любых точек z1,z2 D, |
удовлетворяю- |
||||||||||||||||||||||
щих |
условию |
|
z1 z2 |
|
, |
|
|
выполняется |
неравенство |
|||||||||||||||
|
|
|
||||||||||||||||||||||
|
f z1 f z2 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 4iz 3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пример 11. Вычислить предел |
lim |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
. |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z i |
z i |
|
|
|||||||
|
|
|
|
|
z2 |
4iz 3 |
0 |
|
|
|
z i z 3i |
|||||||||||||
|
|
Решение. lim |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
2i. |
|||||
|
|
|
|
|
|
|
|
|
|
z i |
|
|||||||||||||
|
|
|
|
z i |
|
|
z i |
|
0 |
z i |
|
|
||||||||||||
|
|
Пример 12. Вычислить предел |
lim |
siniz |
. |
|
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
i |
|
ch z ish z |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||
38 |
39 |
