
Учебное пособие 800226
.pdf
Решение.
|
|
lim |
|
|
|
siniz |
|
|
lim |
|
|
|
|
|
|
|
|
|
siniz |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
z |
i |
|
|
ch z ish z |
|
|
z |
i |
|
cosiz siniz |
|
|
|
|
|
|
2 2 |
2 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2iz 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Пример 13. Вычислить предел |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
eiz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
e2iz |
|
1 |
|
|
0 |
|
|
z |
|
|
lim |
e2i i 1 |
lim |
1 e2i |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
lim |
|
|
|
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
iz |
|
|
|
0 |
|
|
|
|
|
|
i |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
e |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ie |
|
|
|
i |
|
|||||||||||||||||||||||||||||||
z |
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 cos2 isin2 |
|
|
2sin2 i2sin cos |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
i lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
0 1 cos isin |
|
|
|
|
|
|
|
|
|
0 2sin2 |
i2sin |
cos |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
sin sin icos |
|
|
|
|
|
2sin |
|
|
cos |
|
|
|
i |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
i lim |
|
|
|
i lim |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2i . |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
icos |
|
0 |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
sin |
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2.3. Дифференцирование функций комплексного переменного
Пусть функция w f z определена в некоторой облас-
ти D комплексной плоскости z . Пусть точки z и z z
принадлежат области D. Обозначим w f z z f z ,
z x i y.
Определение 1. Функция w f z называется диффе-
ренцируемой в точке z D, если отношение |
w |
имеет конеч- |
|
||
|
z |
|
40 |
|
|
ный предел при z, |
стремящемся к нулю произвольным обра- |
|||||||||||
зом. Этот предел называется производной функции |
f z в |
|||||||||||
данной точке z и обозначается f |
|
z (или |
df |
|
|
dw |
), так |
|||||
|
|
|
||||||||||
|
|
|
, w , |
dz |
||||||||
|
|
|
|
|
|
w |
|
dz |
|
|||
что по определению |
f |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
z w lim |
z |
|
|
|
|
|
|||||
|
|
|
z 0 |
|
|
|
|
|
|
|||
Если z x iy, |
w f z u x, y iv x, |
y , то в каждой |
||||||||||
точке дифференцируемости функции |
f z выполняются со- |
|||||||||||
отношения u v и u v , называемые условиями Коши-
x y y x
Римана (Даламбера-Эйлера). Обратно, если в некоторой точке
x, y функции |
u x, y |
|
и |
v x, |
y |
дифференцируемы как |
||||||||||||||||||
функции действительных переменных |
|
x и y и, кроме того, |
||||||||||||||||||||||
удовлетворяют условиям Коши-Римана, |
то функция f z яв- |
|||||||||||||||||||||||
ляется дифференцируемой в точке z x iy |
как функция ком- |
|||||||||||||||||||||||
плексного переменного z . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть z rei , |
тогда f z u r, iv r, , и условия |
|||||||||||||||||||||||
Коши-Римана в полярных координатах имеют вид |
||||||||||||||||||||||||
|
|
u |
|
1 |
|
v |
, |
|
v |
|
1 |
|
|
u |
. |
|
|
|
||||||
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
r |
|
r |
|
r |
|
|
|
||||||||||||||
|
f z |
r |
u |
|
|
v |
1 v |
|
u |
|||||||||||||||
Следовательно, |
|
|
|
i |
|
|
|
|
|
|
|
i |
|
. |
||||||||||
z |
|
r |
z |
|
|
|||||||||||||||||||
|
|
|
|
|
r |
|
|
|
|
|
|
|||||||||||||
Определение 2. Функция w |
f z |
называется аналити- |
||||||||||||||||||||||
ческой в данной точке z D, если она дифференцируема как в самой точке z , так и в некоторой ее окрестности. Функция w f z называется аналитической в области D, если она
дифференцируема в каждой точке этой области.
Для любой аналитической функции f z имеем
41
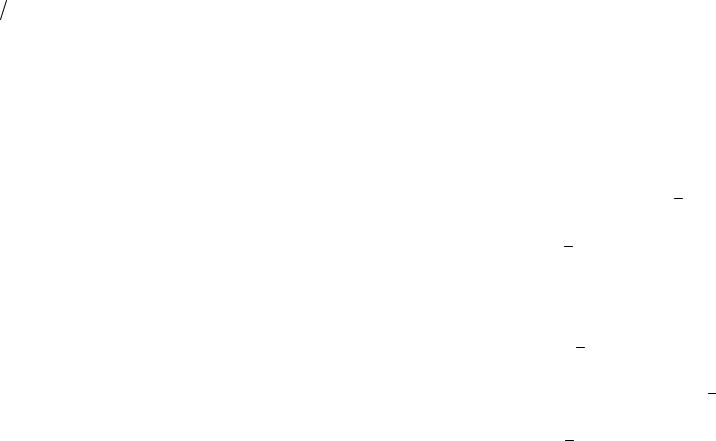
f z |
u |
i |
v |
|
v |
i |
u |
|
u |
i |
u |
|
v |
i |
v |
. |
|
|||||||||||||||
|
|
|
|
|
|
|
|
y |
|
|
||||||||||||||||||||||
|
x |
|
x |
|
y |
|
|
y |
|
|
|
x |
y |
|
|
x |
|
|||||||||||||||
Если f z |
и g z |
|
– аналитические в области D функ- |
|||||||||||||||||||||||||||||
ции, то функции |
f z g z , |
|
|
f z g z |
также аналитичны в |
|||||||||||||||||||||||||||
области D, а частное f z |
|
g z |
|
– аналитическая функция во |
||||||||||||||||||||||||||||
всех точках области D, |
в которых g z 0. При этом имеют |
|||||||||||||||||||||||||||||||
место формулы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f z g z f z g z , |
|
|
|
|
|||||||||||||||||||||||||
f z g z f z g z f z g z , |
|
|||||||||||||||||||||||||||||||
|
|
z |
|
|
|
|
z g z f z g |
|
z |
|
|
|
|
|
||||||||||||||||||
f |
|
f |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
g |
z |
|
|
|
|
|
|
|
|
|
g |
z |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Если w f z |
– аналитическая в области |
D функция с |
||||||||||||||||||||||||||||||
областью значений G f z |
|
z D |
и функция w |
анали- |
||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
тична в области |
G , |
то сложная функция |
|
|
F z f |
z – |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аналитична в области D. Производная этой функции находит- |
||||||||||||||||||||||||||||||||
ся по обычному правилу: |
|
F z |
dF |
|
dw |
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dw |
dz |
|
|
|
|
|
|
|
|
|
|
|||||
Формулы |
дифференцирования |
аналитических функций |
||||||||||||||||||||||||||||||
комплексного |
переменного |
|
аналогичны |
|
|
соответствующим |
||||||||||||||||||||||||||
формулам дифференцирования функций действительного переменного. Так zn nzn 1, ez ez , Lnz 1 z ,
z ,
sin z cosz, cosz sin z , sh z ch z , ch z sh z .
Пример 14. Показать, что функция f z z3 аналитична
во всей комплексной плоскости (кроме z ) и найти ее производную.
42
|
|
|
Решение. |
f z x iy 3 x3 3ix2y 3xy2 iy3 , |
поэто- |
|||||||||||||
му |
действительная |
часть |
|
u x3 3xy2 , а |
мнимая |
часть |
||||||||||||
v 3x2y y3. |
Проверим выполнение условий |
|
Коши-Римана, |
|||||||||||||||
для |
чего |
найдем |
частные |
|
производные: |
|
u |
3x2 |
3y2 , |
|||||||||
|
|
|
||||||||||||||||
|
v |
|
|
|
|
|
|
|
u |
|
|
v |
|
|
x |
|
||
|
3x |
2 |
3y |
2 |
, |
6xy, |
6xy. Видно, что условия Ко- |
|||||||||||
|
y |
|
|
y |
x |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ши-Римана выполняются во всей комплексной плоскости, так
как |
u |
|
v |
и |
u |
|
v |
. Следовательно, функция аналитична |
x |
y |
y |
|
|||||
|
|
|
|
x |
||||
во всей комплексной плоскости. Найдем производную данной
функции: |
f z |
u |
i |
v |
3x2 |
3y2 i6xy 3 x iy 2 3z2 . |
|||||||||
|
|
||||||||||||||
|
|
|
x |
x |
|
|
|
|
|
|
|
|
|
||
Пример 15. Проверить функцию f z zz |
на аналитич- |
||||||||||||||
ность. |
|
|
|
|
f z zz |
|
|
x iy x iy x2 y2 , |
|
||||||
Решение. Имеем |
|
|
так |
||||||||||||
что u x2 |
y2 , |
v 0. |
Условия Коши-Римана в этом случае |
||||||||||||
|
2x 0 |
|
|
|
|
|
|
|
|
|
|
0 . |
|||
примут вид |
|
|
и удовлетворяются только в точке 0, |
||||||||||||
|
2y 0 |
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, |
функция f z zz |
дифференцируема только в |
|||||||||||||
точке z 0 и нигде не аналитична. |
|
||||||||||||||
Пример 16. Проверить |
|
|
|
функцию f z |
z |
Rez |
на |
||||||||
аналитичность. |
|
|
|
f z |
|
|
Rez x iy x x2 ixy , |
|
|||||||
Решение. |
Имеем |
z |
так |
||||||||||||
что u x2 , |
v xy . Условия Коши-Римана в этом случае при- |
||||||||||||||
2x x |
|
|
|
|
|
|
|
|
|
|
0 . |
||||
мут вид |
|
|
и удовлетворяются только в точке 0, |
||||||||||||
|
0 y |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
43 |
|
|
|
|
|
|
|
|
||

Следовательно, функция f z zz дифференцируема только в
точке z 0 и нигде не аналитична.
Определение 3. Функция x, y называется гармониче-
ской в области D, если она имеет в этой области непрерывные частные производные до второго порядка включительно и удовлетворяет в этой области уравнению Лапласа
x, y |
2 |
|
2 |
0. |
|
x2 |
y2 |
||||
|
|
|
|||
Если функция f z u iv |
аналитична в некоторой об- |
||||
ласти D, то ее действительная часть u x, y и мнимая часть
v x, y являются гармоническими в этой области функциями.
Это следует из условий Коши-Римана.
Аналитическую функцию f z можно восстановить, ес-
ли известна ее действительная часть u x, y или мнимая часть
v x, y . Для этого применяются различные способы.
1) Если функция f z аналитична в окрестности точки
z0 и f z0 C0 , то ее можно восстановить по одной из сле-
дующих формул
z |
z |
|
|
|
z |
z |
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||||||
f z 2u |
0 |
, |
|
|
|
|
C0, |
|||||||||
|
|
|
|
2i |
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
z |
z |
|
|
z |
z |
0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
f z 2iv |
|
0 |
, |
|
|
|
|
C0 . |
||||||||
|
2i |
|
|
|||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
2) Пусть известна функция |
u x, y |
– действительная |
||||||||||||||
часть аналитической в области D функции |
|
f z . Чтобы вос- |
||||||||||||||
становить функцию f z , необходимо найти ее мнимую часть
v x, |
y . Запишем v x, y dv C |
v |
dx |
v |
dy C . Отсю- |
||||||||
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x |
y |
|||
да, пользуясь условиями Коши-Римана, получаем |
|||||||||||||
|
v x, y |
u |
dx |
u |
dy C . |
||||||||
|
|
|
|
|
|||||||||
|
|
|
y |
|
x |
|
|
||||||
|
AB |
|
|
|
|
|
|
|
|
||||
Здесь точка A x0, y0 фиксирована, а точка |
B x, y произ- |
||||||||||||
вольная, A D и B D , интеграл не зависит от вида кривой |
|||||||||||||
AB , |
C – произвольная постоянная, которая находится из до- |
||||||||||||
полнительного условия f z0 C0 . |
|
|
|
|
|
|
|
|
|||||
|
Если известна мнимая часть v x, y аналитической в об- |
||||||||||||
ласти D функции f z , то аналогично получаем |
|||||||||||||
|
u x, y |
v |
dx |
v |
dy C. |
|
|
||||||
|
|
|
|
|
|||||||||
|
|
y |
x |
|
|
||||||||
|
AB |
u x, y – |
|
|
|||||||||
|
3) Пусть известна функция |
действительная |
|||||||||||
часть аналитической в области D функции f z . Найдем u .
|
|
|
|
|
|
|
|
|
|
v |
|
u |
|
x |
|
Из первого условия Коши-Римана получаем |
|
|
. Отсюда |
||||||||||||
|
y |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
v x, y |
v |
dy x , |
где функция |
x |
пока неизвестна. |
||||||||||
|
|||||||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||
Дифференцируя v x, y |
по x |
и используя второе условие Ко- |
|||||||||||||
|
|
|
|
v |
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ши-Римана, получим |
|
|
dy |
x |
|
|
, откуда находим |
||||||||
y |
y |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x . Интегрируя, |
определяем x x dx C . |
Таким |
|||||||||||||
образом, функция v x, y , а, |
следовательно, |
и функция |
f z , |
||||||||||||
определена с точностью до константы C , которая находится из
44 |
45 |

дополнительного условия f z0 C0 . Заметим, что можно на-
чать решение с нахождения производной u .
y
Если известна мнимая часть v x, y , то действительная часть u x, y находится аналогично вышеизложенному.
Пример 17. Проверить, что функция u x,y y3 3x2y
является вещественной частью аналитической функции f z и
найти эту функцию, f 0 i.
|
|
Решение. |
Найдем производные: |
u |
6xy, |
2u |
6y, |
|||||||||
|
|
x |
|
|
x2 |
|||||||||||
|
|
|
|
2u |
|
|
|
|
|
|
|
|
|
|||
|
u |
3y2 3x2 , |
|
6y |
Функция u x, y |
|
является гармони- |
|||||||||
|
|
|
|
|
||||||||||||
|
y |
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
||
ческой во всей |
|
плоскости, так как |
2u |
|
|
2u |
6y 6y 0 . |
|||||||||
|
x2 |
y2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, она является действительной частью некото-
рой |
аналитической |
функции, |
|
т.е. |
|
найдется |
такая |
функция |
||||||||||||||||||||||||
v x, y , что f z u iv. Решим задачу тремя способами. |
||||||||||||||||||||||||||||||||
|
1) f z 2u |
z |
z0 |
|
, |
z |
z |
0 |
|
C |
|
|
, где |
z |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
0, C |
|
i. То- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
2i |
|
|
|
|
|
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
z |
|
z |
|
|
|
|
|
z3 |
|
|
|
z3 |
|
|
|
|
|
|
|
|
|
||||||||||
гда |
f z 2u |
|
, |
|
|
|
|
i |
2 |
|
|
6 |
|
|
|
|
i iz3 i . |
|
||||||||||||||
2 |
|
|
|
8i |
8i |
|
||||||||||||||||||||||||||
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
v x, y |
|
|
x,y |
|
|
u |
|
|
|
|
u |
|
|
|
|
|
|
|
||||||||||
|
2) Найдем |
|
|
|
|
dx |
dy C . Подставляя |
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x0,y0 |
|
|
y |
|
|
|
x |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в этот интеграл выражения для производных, получим
46
v x, y |
x,y |
3y2 3x2 dx 6xydy C . |
|
|
Интегрирование |
||
|
x0,y0 |
|
|
проведем по ломаной M0M1M (рис. 1) со звеньями, парал-
лельными координатным осям. За точку M0 x0, y0 примем начало координат, т.е. x0 0 и y0 0, тогда остальные точки
|
|
|
|
|
|
x |
|
M1 x, 0 и |
M x, |
y . Вычисляем интеграл: v x, y 3x2dx |
|||||
|
|
|
|
|
|
0 |
|
y |
|
x |
|
y |
|
|
|
6xydy C x3 |
3xy2 |
C x3 3xy2 C. |
Подставляя |
||||
0 |
0 |
||||||
0 |
|
|
|
|
|
|
|
функции u x,y y3 3x2y и v x, y x3 3xy2 |
C в выра- |
||||||
жение f z u iv, получим |
|
||||||
f z y3 3x2y i x3 3xy2 C i x iy 3 iC iz3 iC . |
|||||||
Из условия |
f 0 i находим C 1 и окончательно получаем |
||||||
f z iz3 i.
y
 M(x,y)
M(x,y)
|
M0(0,0) |
0 |
M1(x,0) x |
Рис. 2.1 47

3) |
Имеем |
u |
6xy. |
|
По |
первому |
из условий |
Коши- |
|||||||||||||
|
|||||||||||||||||||||
|
|
|
x |
|
u |
|
|
v |
|
|
|
|
|
v |
|
|
|
|
|
|
|
Римана |
должно |
быть |
|
|
, |
так |
что |
|
6xy. |
Отсюда |
|||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
x |
|
y |
|
|
|
|
y |
|
|
|
|
|
|||
v x, y 6xy dy 3xy2 |
x , |
где функция |
x |
пока |
|||||||||||||||||
неизвестна. Дифференцируя v x, |
y по x |
|
и используя второе |
||||||||||||||||||
условие |
Коши-Римана, |
|
получим |
3y2 x |
u |
|
|||||||||||||||
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
3y2 3x2 , |
откуда |
x 3x2 . |
Интегрируя, |
определяем |
|||||||||||||||||
x 3x2dx x3 C . |
|
Итак, v x, |
y 3xy2 x3 |
C , |
и, |
сле- |
|||||||||||||||
довательно, |
f z y3 |
3x2y i 3xy2 x3 C iz3 |
iC . Из |
||||||||||||||||||
условия |
f 0 i |
находим |
|
C 1 |
и |
окончательно |
получаем |
||||||||||||||
f z iz3 i.
48
ГЛАВА 3 ИНТЕГРИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
3.1. Основные понятие об интегрировании функций комплексного переменного
|
L |
|
zn-1 |
|
z2 |
|
n |
2 |
|
z1 |
zn |
 1
1
 z0
z0
Рис. 3.1
Пусть на комплексной плоскости задана ориентированная кусочно-гладкая кривая L, на которой определена функция f z . Разобьем эту кривую на n частей zk 1, zk точками z0 ,
z1, , |
zn , пронумерованными в направлении от z0 |
– началь- |
|||
ной точки кривой L, до zn |
– конечной точки кривой L, и на |
||||
каждой |
части выберем |
какую-нибудь |
точку |
k , |
где |
k 1, 2, |
,n (рис.3.1). Обозначим через |
lk (k 1, 2, |
,n) |
||
длину дуги zk 1, zk и пусть l max lk . Составим интеграль-
1 k n
ную сумму
49

|
n |
|
|
|
|
f k zk zk 1 . |
|
(3.1) |
|
|
k 1 |
|
|
|
Если при |
l 0 существует конечный предел интегральных |
|||
сумм (3.1), не зависящий от выбора точек zk |
и k , то тот пре- |
|||
дел называется интегралом от функции f z |
по кривой L: |
|||
|
|
n |
|
|
|
f z dz lim f k zk zk 1 . |
(3.2) |
||
|
L |
l 0k 1 |
|
|
Пусть z x iy, f |
z u x, y iv x, y . Введем обозна- |
|||
чения |
zk xk iyk , |
xk xk 1 xk , |
yk yk 1 |
yk , |
k k i k . Тогда |
|
|
|
|
n |
n |
n |
|
|
f k zk zk 1 uk xk vk yk i vk xk uk yk ,
k 1 |
k 1 |
k 1 |
|
где uk u k , k , |
vk v k, k . Переходя в этом равенстве к |
||
пределу при l 0, получаем |
|
|
|
|
f z dz |
|
|
|
L |
|
|
u x, y dx v x, y dy i v x,y dx u x,y dy, |
(3.3) |
||
L |
L |
|
|
т.е. существование интеграла (3.2) равносильно существованию двух криволинейных интегралов второго рода от действительных функций:
u x, y dx v x, y dy |
и v x, y dx u x, y dy . |
L |
L |
Свойства интегралов.
Из формулы (3.3) следует, что непрерывная на кривой функция интегрируема на этой кривой. Из свойств криволинейных интегралов вытекает также, что имеют место следующие формулы:
1. |
|
af z bg z dz a |
|
f z dz b |
|
g z dz , |
(3.4) |
|
|
|
|
|
|
|
|||
|
L |
|
|
L |
|
L |
|
|
где a и b – любые комплексные числа. |
|
|
|
|||||
2. |
|
|
f z dz f z dz , |
|
|
|
(3.5) |
|
|
L |
L |
|
|
|
|
|
|
т.е. при изменение ориентации кривой интеграл меняет знак.
3. |
f z dz f z dz f z dz . |
(3.6) |
||||||
L1 L2 |
L1 |
|
L2 |
|
|
|
|
|
|
Оценки интегралов |
|
||||||
Лемма 1. Пусть функция |
|
f z |
непрерывна на кривой . |
|||||
Тогда имеет место оценка |
|
|
|
|
|
|
|
|
|
f z dz |
|
f z |
|
dz |
|
, |
(3.7) |
|
|
|
|
|||||
где |
|
dz |
|
|
dx 2 dy 2 ds – элемент дуги кривой . |
|
|||
|
|
|
|||||||
|
|
Следствие. Из неравенства (3.7) вытекает оценка |
|
||||||
|
|
|
|
|
|
f z dz |
|
M l , |
(3.8) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
где M max |
|
f z |
|
, l |
– длина кривой . |
z |
|
|
|
|
|
|
|
|
|||
Лемма 2. Пусть функция f z непрерывна в области D |
|||||
и кривая |
лежит в D. Тогда интеграл f z dz |
можно с |
|
|
|
любой точностью приблизить интегралом от f z |
по лома- |
|
ной, лежащей в области D, т.е. для любого 0 существует ломаная C , лежащая в области D, такая, что
f z dz f z dz . |
(3.9) |
C
50 |
51 |
Лемма 3. Пусть D – ограниченная односвязная область,– граница области D. Если функция f z непрерывна в об-
ласти D вплоть до границы, то интеграл f z dz |
можно с |
|
|
любой точностью приблизить интегралом от f z |
по замк- |
нутой ломаной, лежащей в области D.
Рассмотрим неодносвязную область. Пусть граница
ограниченной области D состоит из кривых |
1, 2, , n : |
|||
n |
k . Если функция |
f z непрерывна |
в области D |
|
k 1 |
|
|
|
|
вплоть до границы , то |
n |
|
|
|
|
|
|
|
|
|
f z dz f z dz. |
(3.10) |
||
|
|
k 1 k |
|
|
Из леммы 3 вытекает |
|
|
|
|
Следствие. Если функция f z |
непрерывна в области D |
|||
вплоть до границы, то интеграл от |
f z по границе области |
|||
D можно с любой точностью приблизить суммой интегралов от f z по замкнутым ломаным, лежащим в области D.
Лемма 4. Кривую , лежащую в области D, можно покрыть конечной системой кругов, принадлежащих области
D. |
|
|
|
|
|
Методы вычисления интегралов |
|
||
Если кривая L задана уравнением |
y y x , то в форму- |
|||
ле (3.3) можно записать dy y x dx и, следовательно, |
||||
|
f z dz |
x2 |
|
|
|
|
|
||
|
|
|
|
|
L |
|
x1 |
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
v |
|
|
|
|
|
|
(3.11) |
|
|
|
|
|
x, y(x) u x, y(x) y (x) dx , |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
где x1 и x2 |
– абсциссы начальной и конечной точек кривой L. |
||||||||||||
Если кривая L задана парой параметрических уравнений |
|||||||||||||
x x t |
и |
|
y y t , |
то |
в формуле (3.3) |
|
можно |
записать |
|||||
dx x t dt , |
dy y t dt |
и, следовательно, |
|
|
|
|
|||||||
|
f |
z dz |
t2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
i |
v |
|
|
|
|
|
, |
(3.12) |
|||
|
|
x(t), y(t) x (t) u x(t), y(t) y (t) dt |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
|
|
|
|
|
|
|
|
где x1 x(t1), x2 |
x(t2). |
|
|
|
|
|
|
||||||
Если |
кривая |
L |
задана параметрическим уравнением |
||||||||||
z z t , |
причем начальная и конечная точки дуги соответст- |
||||||||||||
вуют значениям параметра t t1 |
и t t2 соответственно, то |
||||||||||||
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
|
|
|
|
|
f z dz f z |
|
|
|
|
(3.13) |
||||
|
|
|
|
(t) z (t)dt . |
|
|
|
||||||
|
|
|
|
L |
|
|
t1 |
|
|
|
|
|
|
Если путь интегрирования является полупрямой, выходящей из точки z0 , то полезно сделать замену переменной
z z0 rei . В этом случае 0=const, расстояние от точки z0 меняется от 0 до r0 , dz ei 0 dr , поэтому
f z dz ei 0 |
r0 |
dr . |
|
f z0 rei 0 |
(3.14) |
||
L |
0 |
|
|
Если путь интегрирования является или дугой окружности с центром в точке z0 , то также полезно сделать замену пе-
52 |
53 |

ременной z z0 rei . В этом случае r r0 const , угол меня-
ется от 1 до 2 , dz ir0ei d , поэтому
f z dz ir0 |
2 |
f z0 r0ei ei d . |
|
|
|
(3.15) |
|||
L |
|
1 |
|
|
Функция F z |
называется первообразной функции |
f z |
||
в области D, если |
F z |
дифференцируема в этой области и |
||
F z f z z D. |
|
|
|
|
Пусть функция f z |
аналитична в односвязной области |
|||
D, а L – некоторая кривая, целиком лежащая в D. Тогда
1) существует первообразная F z для |
f z в D и вер- |
на формула Ньютона-Лейбница: |
|
f z dz F z2 F z1 , |
(3.16) |
L |
|
где z1 и z2 – начальная и конечная точки кривой L;
2) если L – любой замкнутый кусочно-гладкий контур в
области D, то верна теорема Коши: |
|
f z dz 0; |
(3.17) |
L |
|
Если функции f z и z – аналитические в односвяз-
ной области D, а z1 и z2 – произвольные точки этой области, то имеет место формула интегрирования по частям:
z2 |
|
z z dz f z z |
|
z2 |
|
z2 |
z f z dz . |
|
|
|
f |
|
|
|
(3.18) |
||||
|
|
|
|
z |
|
|
|
||
z |
|
|
1 |
|
z |
|
|
||
1 |
|
|
|
|
|
|
1 |
|
|
Замена переменных в интегралах от функций комплексного переменного производится аналогично случаю функции действительного переменного. Пусть аналитическая функция
z w отображает взаимно однозначно контур C1 |
в плоско- |
|||||
сти w |
на контур C в плоскости z . Тогда |
|
||||
|
|
f z dz |
|
f w w dw. |
(3.19) |
|
|
|
|
|
|
||
|
C |
|
C1 |
|
|
|
1 2
D
3
|
Рис. 3.2 |
Если функция f z |
аналитична в многосвязной области |
D, ограниченной контуром и внутренними по отношению к |
|
нему контурами 1, 2, |
, k , и непрерывна в замкнутой об- |
ласти D D 1 k , где знаки в верхних индексах означают направления обходов (рис. 3.2), то верна теорема Коши для многосвязной области:
54 |
55 |

|
|
|
|
|
|
|
|
|
|
|
|
f z dz 0. |
|
|
|
|
|
|
(3.20) |
|||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Вычислить интеграл 1 i 2 |
z |
dz |
по лини- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
ям, соединяющим точки z1 0 и z2 |
1 i , |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
а) по параболе y x2 |
(рис. 3.3, а); |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
б) по прямой (рис. 3.3, б); |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
в) по ломаной z1z3z2, |
z3 1 (рис. 3.3, в). |
|
|
|
||||||||||||||
|
y |
|
|
|
|
|
z2 |
|
|
y |
z2 |
|
|
y |
|
z2 |
|
|||||
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
||||||
|
0 z1 |
|
x |
|
0 z1 |
|
|
x |
0 z1 |
|
z3 |
x |
||||||||||
|
1 |
|
1 |
|
|
1 |
||||||||||||||||
|
|
|
|
|
|
|
|
а) |
|
|
|
б) |
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Запишем подынтегральную функцию в виде |
||||||||||||||||||
1 i 2 |
z |
1 i 2(x iy) (1 2x) i(1 2y) u iv . |
Проверим |
|||||||||||||||||||
эту |
функцию |
на |
аналитичность: |
u |
2, |
|
v |
2. |
Так |
как |
||||||||||||
|
|
|
||||||||||||||||||||
|
u |
|
|
v |
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|||||
|
|
, |
то функция не |
является аналитической. |
Применяя |
|||||||||||||||||
|
|
|
||||||||||||||||||||
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
формулу (3.3), получим
1 i 2z dz (1 2x)dx (1 2y)dy i (1 2y)dx (1 2x)dy.
L L L
а) Для параболы y x2 имеем dy 2xdx (0 x 1). Следовательно,
1 i 2z dz
L
1 |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 2x (1 2x |
|
)2x dx i 1 2x |
|
|
(1 2x)2x dx |
|||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
x 2x2 x4 |
|
1 |
|
|
|
|
2 |
|
|
|
|
1 |
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
i |
x x2 |
|
x3 |
|
|
2 |
|
i . |
|||||||||||
|
|
|
3 |
|
3 |
|||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
б) Уравнение прямой, |
проходящей через точки z1 0 и |
|||||||||||||||||||||
z2 1 i , будет y x |
|
(0 x 1), а значит, |
|
dy dx. Поэтому |
||||||||||||||||||
|
|
|
|
|
1 i 2 |
z |
dz |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
(1 2x) (1 2x) dx i (1 2x) (1 2x) dx |
||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
|
2x2 |
|
1 i 2x |
|
10 2 2i . |
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в) |
На отрезке |
z1z3 : |
|
|
y 0, dy 0, |
|
0 x 1. На отрезке |
|||||||||||||||
z3z2 : x 1, dx 0, 0 y 1. Используя свойство линейности криволинейных интегралов, получим
1 i 2 |
z |
dz |
|
1 i 2 |
z |
dz |
1 i 2 |
z |
dz |
||||||||||||||||
L |
|
z1z3 |
|
|
|
|
|
|
|
|
|
z3z2 |
|
||||||||||||
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
(1 2x)dx i dx (1 2y)dy i (1 2 1)dy |
|||||||||||||||||||||||||
0 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
x x2 |
|
1 ix |
|
10 |
y y2 |
|
1 i y |
|
10 2. |
|
|||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
z |
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример 2. Вычислить I e |
|
|
Rezdz , где C – отрезок |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
прямой, соединяющей точки z1 0 и z2 |
1 i . |
|
|||||||||||||||||||||||
Решение (первый способ). Выделим действительную и |
|||||||||||||||||||||||||
мнимую часть подынтегральной функции f z e |
|
z |
|
2 |
Rez. Для |
||||||||||||||||||||
|
|
||||||||||||||||||||||||
|
|
||||||||||||||||||||||||
56 |
57 |

этого перепишем ее в виде e |
|
z |
|
2 |
Rez ex2 y2 x. Отсюда следует, |
|||||
|
|
|||||||||
|
|
|||||||||
u x, y xex2 y2 |
, |
v x, y 0. Применим формулу (3.3). Полу- |
||||||||
чаем |
|
|
|
|
|
|
|
|
||
e |
|
z |
|
2 |
Rezdz xex2 y2 dx i xex2 y2 dy . |
|||||
|
|
|||||||||
|
|
|||||||||
C |
|
|
C |
C |
||||||
Уравнение прямой, проходящей через точки z1 0 и z2 1 i , будет y x, а значит dy dx. Поэтому
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 i |
1 |
|
|
|
|
1 |
|||||||||||
|
|
|
|
|
|
|
I xe2x2 dx i xe2x2 dx |
|
|
e2x2 |
|
|
e2x2 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
0 |
4 |
|
|
|
|
0 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
e2 1 i |
1 |
e2 1 |
1 |
e2 1 1 i . |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
4 |
4 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Решение (второй способ). Так как при движении вдоль |
||||||||||||||||||||||||||||||||||||||||||||||||||||
отрезка C изменяется только r |
z |
|
|
|
от |
|
0 до |
|
2 |
, а argz |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 i dr , |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
, |
|
|
то z re 4 , |
dz e 4dr |
|
|
|
|
|
|
Rez rcos |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
||||||||||
|
|
2 |
|
r |
и для интеграла получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
I er2 |
|
|
|
|
|
r |
|
|
1 i dr |
1 i |
er2 d r2 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 i |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 i er2 |
|
|
|
2 |
e2 1 . |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
0 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
Пример 3. Вычислить |
zkdz, где C – окружность еди- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ничного радиуса с центром в точке z 0 (обход против часовой стрелки, k – целое число).
58
Решение. Так как на окружности C |
имеем |
|
z |
1, то |
|||
z ei |
(0 2 ) и dz iei d . Тогда получаем |
|
|
|
|||
|
|
2 |
2 |
0, |
k 1 |
||
|
|
|
|
||||
|
zkdz eik iei d i ei k 1 d |
. |
|||||
|
C |
0 |
0 |
2 i, |
k 1 |
||
При k 0 результат вычислений согласуется с теоремой Коши
(3.17). При k 1 функция |
f z |
1 |
не определена и не диф- |
|
|||
|
|
z |
|
ференцируема в точке z 0. Интеграл не равен нулю. При k 2, 3, подынтегральная функция не определена в точке
z 0 и теорема Коши также не применима, |
но интеграл равен |
||||||||||||||||||
нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 4. Вычислить |
zzdz , где C : |
|
z |
|
1. |
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|||||
Решение. Аналогично примеру 3: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
||||
|
zzdz ei e i iei d ei d i |
ei |
|
||||||||||||||||
0 |
|
||||||||||||||||||
|
|
|
|||||||||||||||||
C |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
e2 i |
1 cos2 isin2 1 0. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 i |
|
|
|
|
|
|
|
|
|
Пример 5. Вычислить интеграл zdz . |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
Решение. Так как подынтегральная функция является |
|||||||||||||||||||
аналитической, |
то |
можно |
использовать |
формулу |
Ньютона- |
||||||||||||||
|
|
1 i |
|
|
z2 |
|
1 i |
|
|
|
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Лейбница (3.16): |
|
zdz |
|
|
|
1 |
1 i 2 |
i2 |
i . |
||||||||||
|
|
|
|
|
|||||||||||||||
|
|
i |
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3.2. Интегрирование многозначных функций |
|||||||||||||||||||
Пусть функция |
w f z , аналитическая в области D, |
||||||||||||||||||
отображает D на область G и такова, что обратная функция
59
