Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

Математика

Файл:

Функции комплексного переменного. Дежин В.В., Лапшина М.Л

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

1.02 Mб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

В.В. Дежин М.Л. Лапшина

ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Учебное пособие

Воронеж 2011

ФГБОУВПО «Воронежский государственный технический университет»

В.В. Дежин М.Л. Лапшина

ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Утверждено Редакционно-издательским советом университета в качестве учебного пособия

Воронеж 2011

УДК 517

Дежин В.В. Функции комплексного переменного: учеб. пособие / В.В. Дежин, М.Л. Лапшина. Воронеж: ФГБОУВПО «Воронежский государственный технический университет», 2011. 133 с.

Учебное пособие состоит из пяти глав, разбитых на параграфы. Оно содержит теоретический материал по разделу функции комплексного переменного, а также примеры решения задач.

Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 230200 «Информационные системы», специальности 230201 «Информационные системы и технологии», дисциплине «Математика».

Предназначено для студентов очной формы обучения. Учебное пособие подготовлено в электронном виде в тек-

стовом редакторе MS Word и содержится в файле ФКП.pdf.

Ил. 31. Библиогр.: 15 назв.

Научный редактор д-р физ.-мат. наук, проф. И.Л. Батаронов

Рецензенты: кафедра информационных систем и технологий Воронежского института высоких технологий (зав. кафедрой д-р техн. наук, проф. Ю.С. Сербулов); д-р физ.-мат. наук, проф. В.Н. Нечаев

©Дежин В.В., Лапшина М.Л., 2011

©Оформление. ФГБОУВПО «Воронежский государственный технический университет», 2011

ВВЕДЕНИЕ

Раздел «Функции комплексного переменного» является одним из наиболее важных и сложных при изучении курса «Математика». Глубокое неформальное изучение таких основных понятий как комплексные числа, кривые и области на комплексной плоскости, основные элементарные функции комплексного переменного, дифференцирование функций комплексного переменного, интегрирование функций комплексного переменного, разложение функций комплексного переменного в ряды Лорана, применение вычетов к вычислению контурных интегралов и определенных интегралов необходимо при усвоении специальных курсов для специальности «Информационные системы».

Вглаве 1 пособия содержатся необходимые теоретические сведения по комплексным числам и действиям с ними.

Во 2-й главе пособия определяются основные элементарные функции комплексного переменного, вводится понятие аналитических функций комплексного переменного и их дифференцирования.

В3-й главе пособия излагается понятие интегрирования функций комплексного переменного, применение интегральной формулы Коши.

В4-й главе пособия изучается разложение функций комплексного переменного в ряды Лорана. Проводится классификация изолированных особых точек, определяется вычисление вычетов в изолированных особых точках.

В5-й главе рассматриваются вычеты и их приложение к вычислению интегралов.

Главы пособия разбиты на параграфы, в каждом из которых приведены примеры решения задач.

Пособие может использоваться как студентами, так и преподавателям для подготовки к практическим занятиям, контрольным работам, коллоквиуму, экзамену.

ГЛАВА 1 КОМПЛЕКСНЫЕ ЧИСЛА. КОМПЛЕКСНАЯ ПЛОСКОСТЬ

1.1. Определение комплексного числа

Комплексными числами называются пары x, y действи-

тельных чисел x и y , если для них определены понятия равенства и операции сложения и умножения следующим обра-

зом:		Два комплексных числа x1, y1 и x2,		y2
	1.	Два комплексных числа x1, y1 и x2,		y2	считаются
равными тогда и только тогда, когда
		x1 x2 и y1 y2.			(1.1)
	2.	Суммой двух комплексных чисел x1,		y1	и x2, y2
называется комплексное число
		x1 x2,	y1 y2		(1.2)
	3.	Произведением двух комплексных чисел			x1, y1 и
x2,	y2	называется комплексное число
		x1x2 y1y2,	x1y2 x2y1 .		(1.3)
	Из формул (1.2) и (1.3) вытекают соотношения:
	x1, 0 x2, 0 x1 x2, 0 ,		x1, 0 x2, 0 x1x2, 0 ,

которые показывают, что операции над комплексными числами вида x, 0 совпадают с операциями над действительными

числами x. Поэтому комплексные числа вида x, 0 отождест-

вляются с действительными числами: x, 0 x .

Комплексное число 0,1 1 называется мнимой еди-

ницей и обозначается буквой i, т.е. i 0, 1 . Для произведения

i2 по формуле (1.3) имеем i2 i i 0,1 0,1 1, 0 1.

Из формул (1.2) и (1.3) вытекают также равенства: 4

0, y 0, 1 y, 0 iy,

x, y x, 0 0, y x iy.

Таким образом, каждое комплексное число x, y можно

представить в виде x iy. Запись комплексного числа в виде x iy называется алгебраической формой комплексного числа Комплексные числа вида iy называются чисто мнимыми. В

частности, число 0, т.е. комплексное число 0, 0 , является

единственным числом, которое одновременно и действительное и чисто мнимой.

С помощью алгебраической формы комплексного числа формулы (1)–(3) записываются таким образом:

1.x1 iy1 x2 iy2 тогда и только тогда, когда


			x1 x2 и	y1 y2.		(1.4)
2.	x1, y1	+ x2, y2		= x1 x2 i y1 y2 .		(1.5)
3. x1 iy1 x2			iy2 x1x2		y1y2 i x1y2 x2y1 .	(1.6)
Комплексное число x iy принято обозначать одной бук-
вой z ,	т.е. z x iy. Число x называется действительной ча-
стью,	а число	y	– мнимой		частью комплексного	числа
z x iy. Для этих чисел приняты обозначения:
	x Re x iy Rez ,				y Im x iy Imz .

(Обозначения Re и Im являются сокращениями французских слов Réel (действительный) и Imaginaire (мнимый)). Здесь, как

и всюду в дальнейшем, предполагается, что x и				y – действи-
тельные числа.
Комплексное число x iy называется				комплексно
сопряжённым с числом x iy и обозначается:
	z		x iy .	.(1.7)
		x iy

Равенство z z имеет место в том и только в том случае, когда z – действительное число.

z1 z2 x1 x2 i y1 y2 .

Пример 1.1. z 5 3i, тогда

5 3i.

Число

x2 y2 называется модулем комплексного числа

z x iy и обозначается

x iy

x2 y2

(1.8)

Очевидно,

0, причем

0 тогда и только тогда,

когда

z 0. Отметим две формулы

(1.9)

2 ,

(1.10)

которые вытекают из равенств (1.7), (1.8) и равенства zz x iy x iy x2 y2 .

Пример 1.2. z 5 3i, тогда		z				5 3i			52 ( 3)2

34 , zz (5 3i)(5 3i) 25 15i 15i 9i2 25 9 34

z 2 34 2 34.

Операции сложения и умножения комплексных чисел обладают следующими свойствами:

1.	Коммутативность
	z1 z2 z2 z1,	z1z2 z2z1.
2.	Ассоциативность
z1 z2 z3 z1 z2 z3 ,		z1z2 z3 z1 z2z3 .

3 Дистрибутивность

z1 z2 z3 z1z2 z1z3 .

Докажем, например, коммутативность сложения. Пусть z1 x1 iy1, z2 x2 iy2 . Тогда по формуле (1.5) имеем

z1 z2 x1 x2 i y1 y2 , z2 z1 x2 x1 i y2 y1 .

Но по свойству коммутативности сложения действительных

чисел	x1 x2 x2 x1 и	y1 y2 y2 y1.	Следовательно,
z1 z2	z2 z1. Аналогично проверяются остальные свойства.
Из свойств 1-3 вытекает, что операции сложения и ум-
ножения над комплексными числами x iy			обладают фор-

мально такими же свойствами, как если бы число i было действительным. В частности, нет необходимости запоминать формулы (1.5)–(1.6), их можно получить по обычным формулам алгебры. Например, (1.6) вытекает из равенства

x1 iy1 x2 iy2 x1x2 iy1y2 ix2y1 i2y1y2

иравенства i2 1. Числа нуль и единица в множестве комплексных чисел обладают теми же свойствами, что и в множестве действительных чисел. А именно, для любого комплексного числа z имеют место равенства

z 0 z , z 1 z .

В множестве комплексных чисел можно ввести операцию, обратную к операции сложения. Эта операция, как обычно, называется вычитанием. Для любых двух комплексных чисел z1 и z2 существует, и притом только одно, число z , удовлетворяющее уравнению

z z2 z1.

(1.11)

Это число называется разностью чисел z1 и z2 и обозначается z1 z2 . В частности, разность 0 z обозначается z.

Из равенств (1.4) и (1.5) вытекает, что для любых ком-

плексных чисел z1 x1 iy1 и	z2 x2 iy2 уравнение	(1.11)
имеет единственное решение	z x1 x2 i y1 y2 .	Таким
образом,

(1.12)

Операция, обратная умножению, называется делением, а частным двух комплексных чисел z1 и z2 называется такое число z , которое удовлетворяет уравнению

zz2 z1,	(1.13)
и обозначается z1 :z2 или z1 z2 . Докажем, что	уравнение

(1.13) имеет единственное реше6ние для любых комплексных

чисел

и z2 , если

z2 0.

Умножая обе части уравнения

(1.13)

на

число

и используя формулу (1.10), получаем

откуда

умножением

на

число

находим

. Таким образом,

z2 0.

(1.14)

z2z2

Если z1 x1 iy1 и z2

iy2 , то формулу (1.14) можно запи-

сать в виде:

x1 iy1 x2 iy2

x1 iy1

x1x2 y1y2

x2y1 x1y2

x iy

Пример 1.3. Пусть z1 2 3i ,

z2 3 4i.Тогда:

z1 z2 (2 3) i( 3 4) 5 i,

z1 z2 (2 3) i( 3 4) 1 7i ,

z z

2 3i 3 4i 6 8i 9i 12i2 6 i 12 18 i,

2 3i

3 4i

2 3i

6 8i 9i 12i

6 17

3 4i

32 42

3 4i

25 25

1.2. Геометрическая интерпретация комплексного числа

Пусть на плоскости задана прямоугольная система коор-

динат.

Комплексное

число

z x iy

изображается

точкой

плоскости с координатами x,

y , и эта точка обозначается той

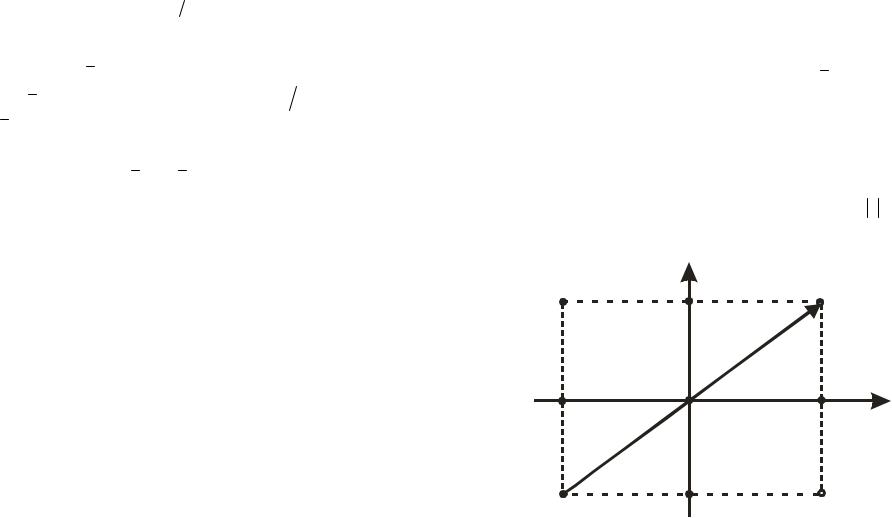
же буквой z (рис. 1.1). Такое соответствие между комплексными числами и точками плоскости является взаимно однозначным. При этом действительные числа изображаются точ-

ками оси абсцисс, а чисто мнимые числа изображаются точками оси ординат. Поэтому ось абсцисс называется действительной осью, а ось ординат – мнимой осью. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ясно, то точки z и z симметричны относительно начала координат, а точки z и z симметричны относительно действительной оси (рис. 1.1). Комплексное число z изображается также вектором с началом в точке 0 и концом в точке z (рис. 1.1).Такое соответствие между комплексными числами и векторами комплексной плоскости также является взаимно однозначным. Поэтому вектор, изображающий комплексное число z , означается той же буквой z . Из формулы (1.8) и рис.1.1 видно, что длина вектора z равна z и име-

ют место неравенства

Rez

Im z

-z z=x+iy y

-x

		_
-z	-y	z
-z	-y

Рис. 1.1

С помощью векторной интерпретации наглядно иллюстрируются сложение и вычитание комплексных чисел. Из фор-

мулы (1.5) вытекает, что число z1 z2 изображается вектором,

построенным по обычному правилу сложения векторов z1 и z2

(рис. 1.2). Вектор z1 z2 строится как сумм векторов z1 и z2

(рис. 1.2). Из рис. 1.2 видно, что расстояние между точками z1 и z2 равно длине вектора z1 z2 , т.е. равно z1 z2 .

z1+z2

z1-z2

-z2

Рис. 1.2

Пример 1.4.

Множество точек z , удовлетворяющих

уравнению

z z0

R, есть окружность радиуса R с центром в

точке z0 , так как

z z0

– расстояние между точками z и z0 .

Пример 1.5.

Множество точек z ,

удовлетворяющих

уравнению

z z1

z z2

, есть множество точек, равноуда-

ленных от точек

и z2 .

Следовательно,

это уравнение пря-

мой, перпендикулярной отрезку, соединяющему точки z1 и z2 , и проведенной через его середину.

Пример 1.6. Множество точек z , удовлетворяющих

уравнению z z1 z z2 2a , где a 2 z1 z2 , есть эллипс с фокусами в точках z1, z2 и с большей полуосью, равной a, так

как

z z1

z z2

– сумма расстояний от точки z до точек z1

и z2 .

Пример 1.7. Аналогично, уравнение

z z1

z z2

2a ,

где a

z z

, является уравнением гиперболы с фокусами

в точках z1, z2

и с действительной полуосью, равной a.

Неравенство треугольника. Для любых комплексных чи-

сел z1 и z2 имеют место неравенства

z1 z2

(1.15)

Доказательство. Длины сторон треугольника с верши-

нами в точках 0, z1, z1 z2 равны

z1 z2

(рис. 2.1).

Следовательно, неравенства (1.15) являются известными из элементарной геометрии неравенствами для длин сторон треугольника.

Следствие. Для любых комплексных чисел z1, z2 ,					, zn
имеет место неравенство
	n	n
	n	n
	zk		zk	.	(1.16)
	k 1	k 1

1.3. Тригонометрическая и показательная формы комплексного числа

Положение точки z x iy на комплексной плоскости однозначно определяется не только декартовыми координатами x, y , но и полярными координатами r . (рис. 1.3), где

– расстояние от точки 0 до точки z , а – угол между

действительной осью и вектором z , отсчитываемый от положительного направления действительной оси. При этом, если отсчет ведется против часовой стрелки, то величина угла считается положительной, а если по часовой стрелке – отрицательной. Этот угол называется аргументом комплексного числа z ( z 0 )и обозначается arg z (обозначение arg является сокращением французского слова argument). Он определяется не однозначно, а с точностью до слагаемого, кратного 2 :

Argz argz 2k							(k 0,		1, 2, ),
где argz есть главное значение Argz ,									определяемое условия-
ми argz , причем
		0,				если		x 0, y 0
		y
	arctg		,			если		x 0,		y 0
		x

		2,				если		x 0, y 0
		y
	arctg			,		если		x 0,		y 0

		x
											(1.17)
argz		,				если		x 0,		y 0

		y				если		x 0,		y 0
arctg					,

		x				если		x 0, y 0
		2,
		y
	arctg		,			если		x 0,		y 0
		x

Из рис. 1.3. видно, что								y rsin .
	x rcos ,										(1.18)

Следовательно, любое комплексное число z 0 можно представить в виде

z r(cos isin ) .

(1.19)

Запись комплексного числа в виде (1.19) называется тригонометрической формой комплексного числа. Из формул (1.18) вытекает, что если z x iy, Arg z, то

cos	x	, sin	y	.	(1.20)

	x2 y2		x2 y2

y	z=x+iy=r(cos isin )=rei
y
	r

	x

	Рис. 1.3
Пример 1.8. Найдем аргумент комплексного числа
z 1 i. Так как точка	z 1 i лежит в третьей четверти и

arctg

arctg1

то по формуле (1.17) получаем

argz

, а

Argz argz 2k

2k ,

где

k 0, 1, 2,

Пример 1.9. Записать в тригонометрической форме ком-

плексное число z 1 i

. Имеем r

( 1)2 (

3)2 2,

argz

arctg

Следовательно,

z 1 i 3 2 cos

isin

Любое комплексное число z 0 можно записать в пока-

зательной форме:

z rei , где r

, Arg z.

(1.21)

Функция ei для любого действительного числа определя-

ется формулой Эйлера

	ei	cos isin .		(1.22)
В частности, e2 i	1,	e i 1, e i/2 i,	e i/2 i ,		ei	1.

Из (1.22) получается равенство
	e i cos isin .			(1.23)

Сложением и вычитанием равенств (1.22) и (1.23) получаются

формулы Эйлера:

cos

ei e i

sin

ei e i

(1.24)

Функция ei

обладает обычными свойствами показательной

функции:

ei 1

i i

)

2 e

1 2

(1.25)

ei n

ei 2

ein ,

n 0, 1, 2,

(1.26)

Из равенств (1.26) и (1.23) вытекает формула Муавра:

cos isin n cosn isinn ,

n 0, 1, 2,

(1.27)

С помощью равенств (1.25) легко получаются формулы умножения и деления комплексных чисел, записанных в показательной форме:

z z	2	rei 1r ei 2			rr ei( 1 2) ,						(1.28)
1	2		1	2		1 2
		z		rei 1	r		i(		)
		1		1	1	e	1	2		.	(1.29)
		z2		r ei 2	r2	e	1	2		.	(1.29)
		z2		r ei 2	r2
				2

Из формулы (1.28) следует, что модуль произведения двух комплексных чисел равен произведению модулей этих чисел: z1z2 z1z2 , а сумма аргументов сомножителей является ар-

гументом произведения: argz1 arg z2 arg(z1z2). Аналогично из формулы (1.29) вытекает, что модуль частного двух ком14

плексных чисел равен частному модулей этих чисел:	z1	z1

	z2	z2

( z2 0), а разность аргументов делимого и делителя является

аргументом частного: argz1 argz2 arg z1 . z2

Пример 1.10. 1 i3 3 1 i 2 2e i 3 3 2ei 4 2

8 2 e i ei 2 16e i 2 16i .

		Пример 1.11. Вычислить													z			z			20	, где			z 1 i						,
		Пример 1.11. Вычислить													z			z			20	, где			z 1 i				3		,
																	1		2						1
z2 1 i .				Имеем			z1								2,					1			3,			z2				,
												1 3																2
												1 3																2
		3 4.		Тогда z			z			20			2e					3		20		210		e 13i 12			20
	2								2				2e
																3		4
					1										2e	3		4
															2e
		10	65i 3	10	22i			i 3				10		i 3						10
2 e				2 e		e					2		e				2				cos		isin
2 e				2 e		e					2		e				2				cos		isin
																						3			3

29 1 i

Корень n-й степени (n – натуральное число) из комплексного числа z 0 имеет n различных значений, которые находятся по формуле

i( 2k )

z n

cos

isin

, (1.30)

где

arg z ,

k 0,1, 2, ,

n 1.

Точки,

соответствующие

этим

значениям,

являются

вершинами

правильного n-

угольника, вписанного в окружность радиуса n

с центром в

начале координат.

Пример 1.12.

Найдем все значения

. Приводим

1 i

комплексное число 1 i к тригонометрическому виду:



1 i	2			cos								isin					.
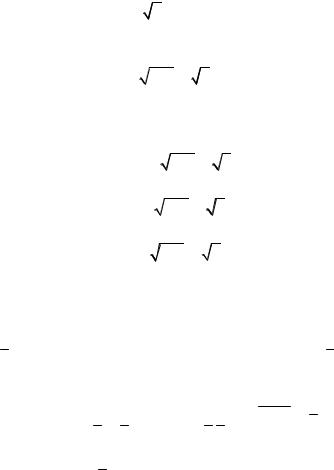
1 i	2			cos								isin					.
										4						4
															2k							2k

													4								4
	31 i					6
Следовательно,							2 cos										isin						.
Следовательно,							2 cos								3		isin					3	.
															3							3

Полагая k 0,1, 2, находим:
		3							6
		3			1 i				6							isin
k 0,											2 cos								,
k 0,											2 cos								,
													12				12
	3							6						7				7
	3		1 i					6						7		isin		7
k 1,										2 cos										,
k 1,										2 cos										,
													12				12
	3							6					15					15
	3							6					15					15
k 2,		1 i							2		cos					isin				.
k 2,		1 i							2		cos		12			isin				.
													12				12

Как уже отмечалось (1.9), модули комплексно сопряженных чисел равны. Установим связь между их аргументами.

Пусть z rei , тогда из равенств (1.22) и (1.23) видно, что z re i . Следовательно, если argz , то argz .

Отметим, что операция сопряжения перестановочна с арифметическими операциями над комплексными числами:

0),

z z

(n 0, 1, 2, ),

z 0

при n 0 .

1.4. Кривые и области на комплексной плоскости

Пусть функция

z (t) определена на отрезке t

и принимает комплексные значения. Эту комплекснозначную

функцию можно	представить	в	виде (t) (t) i (t), где
(t) Re (t) и	(t) Im (t)	–	действительные функции.

Многие свойства действительных функций естественным образом переносятся на комплекснозначные функции.

Предел функции (t) (t) i (t) определяется так

lim (t) lim (t) i lim (t) .

(1.31)

t t0

Таким образом, предел

lim (t)

существует,

если существуют

t t0

пределы lim (t) и lim (t).

t t0

Пределы комплекснозначных функций обладают сле-

дующими свойствами: если существуют пределы lim

(t) a

t t0

и lim 2(t) a2 , то существуют пределы

t t0

(t)

lim

(t) a a

lim

(t)

a ,

(t)

t t0

1 2

а если a

то

lim

1(t)

. Аналогичны определения и

t t0

(t)

свойства пределов

lim (t) и

lim (t).

t t0 0

Функция

(t) (t) i (t)

называется

непрерывной

точке (или на отрезке), если в этой точке (на отрезке) непрерывны функции (t) и (t) . Ясно, что сумма, разность и произведение непрерывных комплекснозначных функций являются непрерывными функциями, а частное двух непрерывных комплекснозначных функций является непрерывной функцией в тех точках, в которых знаменатель не равен нулю. Отметим также, что комплекснозначная функция (t), непрерывная на

отрезке , ,	ограничена на этом отрезке:		(t)	M для не-
которого M 0	и всех t ,	.
Производная функции (t) (t) i (t)			определяется так
			(1.32)
	(t) (t) i (t).		(1.32)

Следовательно, производная (t) существует, если существуют производные (t) и (t). Это определение эквивалентно определению производной с помощью формулы

						(t t) (t)						.		(1.33)

	(t) lim								t
				t 0					t
Если существуют производные 1(t)										и 2(t), то существуют
производные									,
производные	1 2			1			2		,	1 2			1 2	1 2 , а

			1		1			2		2
если 2(t) 0	, то		1		1			2	1	2	.
если 2(t) 0	, то	2						22			.
		2						22

Однако не все свойства дифференцируемых действительных функций переносятся на комплекснозначные функции. В частности, для комплекснозначных функций теоремы Ролля и Лагранжа, вообще говоря, неверны.

Пример 1.13.	Функция (t) eit дифференцируема на
		it	,		1	при всех t 0, 2 . Та-

отрезке 0, 2 , (t) ie				(t)
	не обращается в нуль ни в одной точке от-
ким образом, (t)
резка 0, 2 , хотя (0) (2 ) 1.
Комплекснозначную			функцию			(t) (t) i (t) можно

рассматривать как вектор-функцию (t), (t) . Рассмотрен-

ные выше определения предела, непрерывности и производной для функции (t) являются обычными определениями соответствующих понятий для вектор-функции, сформулированные в терминах комплексных чисел. Комплекснозначная функция z (t), t , отображает отрезок , на не-

которое множество точек комплексной плоскости, которое можно рассматривать как график этой функции. В частности, если функция z (t) непрерывна, то ее графиком является некоторая кривая на комплексной плоскости.

Пусть на конечном отрезке t задана непрерывная комплекснозначная функция z (t). Тогда говорят, что зада-

на непрерывная кривая
z (t),	t ,	(1.34)

а уравнение (1.34) называется параметрическим уравнением этой кривой. При этом, если z1 (t1) и z2 (t2), гдеt1 t2 , то говорят, что точка z2 кривой (1.34) следует за точкой z1. Таким образом, кривая (1.34) является упорядоченным множеством точек комплексной плоскости. Другими словами, кривая (1.34) всегда считается ориентированной в направлении возрастания параметра t. Направление движения точки z вдоль кривой (1.34), соответствующее возрастанию параметра t, называется положительным. Пусть кривая задана уравнением (1.34). Тогда на комплексной плоскости точки z (t), t , образуют некоторое множество M( ). Это множество отличается от самой кривой, во-первых тем, что кривая является упорядоченным множеством точек.

Пример 1.14. Кривая			z eit , 0 t является полуок-
ружностью	z	1, Im z 0,	ориентированной против часовой

стрелки (рис. 1.4).

Второе отличие кривой от множества M( ) состоит в том, что различным точкам кривой может отвечать одна и та

же точка плоскости:	если (t1) (t2) при t1 t2 , то точки
z1 (t1) и z2 (t2)	являются различными на кривой , но

как точки плоскости они совпадают. Такие точки называются

точками самопересечения кривой (1.34). Исключением являет-

ся совпадение начала и конца кривой: если ( ) ( ) , то эта точка не считается самопересечением кривой (1.34). Кривая, не имеющая точек самопересечения, называется простой кривой. Кривая, у которой начало и конец совпадают, называется замк-

нутой кривой.

Кривая в примере 1.14 является простой незамкнутой. 19

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете Математика