
Учебное пособие 800222
.pdf
3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ
3.1 Понятие устойчивости
Любая САУ характеризируется переходным процессом, который возникает при выходе системы из состояния равновесия из-за некоторого воздействия. Переходный процесс x(t) зависит от свойств самой системы и от вида возмущающего воздействия. В переходном процессе можно выделить две составляющие:
x(t)=xв(t)+xсв(t) |
(3.1) |
где xв(t) - движение САУ, определяемое возмущающим воздействием и свойствами самой системы, а xсв(t) – свободные движения системы, определяемые начальными условиями и свойствами самой системы. Основной динамической характеристикой САУ является ее устойчивость. Устойчивость – это свойство системы возвращаться к состоянию установившегося равновесия после устранения возмущения, которое вывело систему из этого состояния.
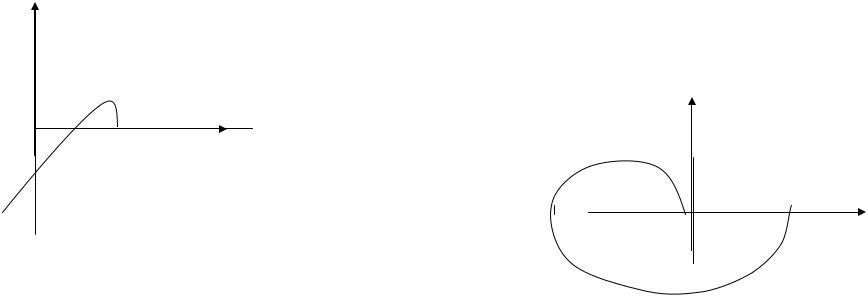
Например, иллюстрацией неустойчивого состояния является рис. 3.1 (при малейшем воздействии шарик теряет устойчивость).
Рис. 3.1
39
Пример устойчивого при любых воздействиях состояния на рис. 3.2.
Рис. 3.2
Возможно также состояние неустойчивого равновесия, при котором система сохраняет устойчивость только при малых воздействиях (рис. 3.3).
Рис. 3.3
3.2.Математическая постановка задачи
Математически САУ будет устойчивой, если
lim xсв(t)=0 , |
|
(3.2) |
|
t |
|
|
|
в противном случае система неустойчива. |
|
||
Свободное |
движение |
системы |
описывается |
дифференциальным уравнением , которое для линейных САУ имеет вид
40
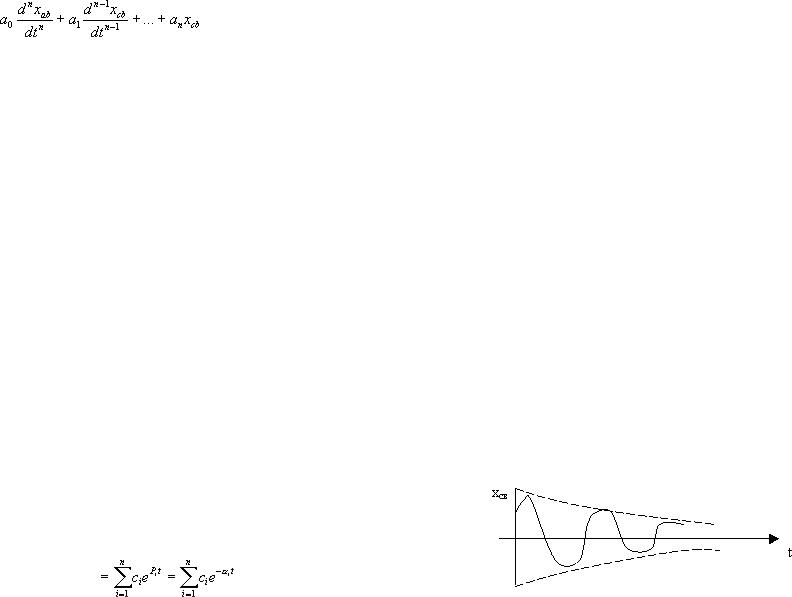
= 0, (3.3)
где коэффициенты аi постоянны (i=1,...,n). Решение дифференциального уравнения (3.3) имеет вид:
хсв(t)= c 1 exp(p1t) + c 2 exp(p2t) |
+...+ c n exp(pnt) |
(3.4) |
|
где ci , i=1,…,n |
постоянные |
интегрирования, |
которые |
определяют из начальных условий, а рi , i=1,…,n - |
корни |
||
характеристического уравнения САУ. |
|
||
Характеристическое уравнение системы имеет вид: |
|||
a 0 р n + a 1 р n-1 +...+ a n-1 р + а n = 0 . |
(3.5) |
||
В зависимости от вида корней уравнения (3.5) переходный процесс будет затухающим или расходящимся и, соответственно, система будет устойчивой или неустойчивой.
3.2Оценка устойчивости САУ по корням характеристического уравнения
При оценке устойчивости необходимо рассмотреть три возможных случая.
1.Корни вещественны.
2.Пары комплексно-сопряженных корней.
3.Корни чисто мнимые.
Если все корни вещественные и отрицательные, то есть
р i = - i, i= 1,…,n, άi >0
в этом случае
хсв(t) |
. |
(3.6) |
|
||
|
41 |
|
Если все корни вещественные и отрицательные, то каждое слагаемое хсв в формуле (3.6) стремится к нулю при t и, следовательно, хсв(t) 0, то есть необходимое и достаточное условие устойчивости (3.2) выполнено и САУ устойчива.
Если все корни вещественные, но среди них имеется хотя бы один положительный корень р к = к 0 , то соответствующее ему слагаемое в (3.6) будет иметь вид ск exp(кt) и будет стремиться к при t .
При этом, хотя все слагаемые в хсв(t) , кроме одного, будут затухать, переходный процесс САУ в целом будет расходящимся, а САУ - неустойчивой.
Если все корни вещественные, отрицательные и есть пара
комплексносопряженных корней |
р |
k =-+j |
. р k+1=- -j . |
||
Тогда комплексным |
корням |
в |
|
Хсв(t) |
соответствуют |
слагаемые А= ск exp[-(-j )t] и |
B= ск exp[-( +j )t]. C учѐтом |
||||
формул Эйлера можно записать |
|
|
|
|
|
А+В= De-a tsin( t+ ). |
|
|
|
(3.7) |
|
Сумма слагаемых, соответствующих комплексносопряжѐнным корням, представляет собой гармоническую функцию с угловой частотой и амплитудой De-a t.
Параметр - это параметр затухания огибающей k – кривой переходного процесса.
при 0
Рис. 3.4
42
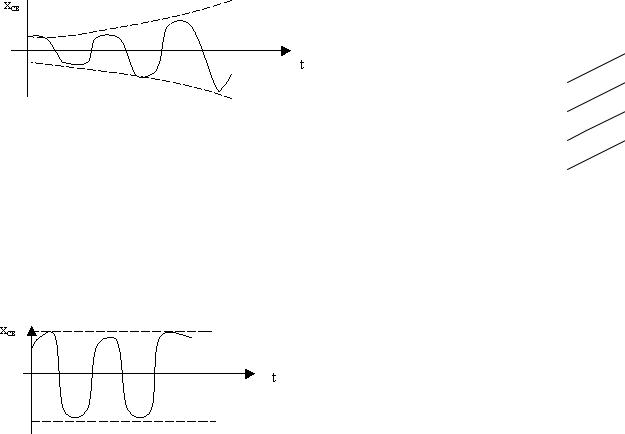
при >0
Рис. 3.5
Таким образом, если действительная часть комплексного корня , САУ устойчива, в противном случае - нет.
В случае чисто мнимых корней и р к =j . р k+1=-j . Составляющая, соответствующая данным корням в хсв(t)
имеет вид
скexp(j )+скexp(-j )=Аsin(t+ ). |
(3.8) |
Таким образом, имеем незатухающие колебания с угловой частотой и постоянной амплитудой А (рис. 3.6).
Рис. 3.6
Таким образом, можно сформулировать критерий устойчивости для устойчивости линейных САУ необходимо и достаточно, чтобы все вещественные корни и все вещественные части комплексных корней характеристического уравнения (3.5) были отрицательными, а если хотя бы один вещественный корень или вещественная часть хотя бы одной пары комплексных корней положительны, то переходный процесс будет расходящимся и САУ будет неустойчивой.
43
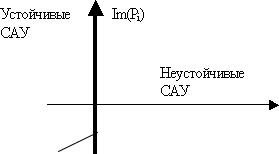 Re(Pi)
Re(Pi)
Рис. 3.7
Наглядно графически необходимые и достаточные условия устойчивости САУ можно представить, изобразив корни (3.5) в комплексной плоскости. Для устойчивости САУ необходимо и достаточно чтобы все корни лежали в левой полуплоскости (рис. 3.7). Если корни находятся на мнимой оси, то говорят, что САУ находится на границе устойчивости.
На практике большинство САУ являются нелинейными, то есть реальные характеристики звеньев и реальные дифференциальные уравнения приходится приближенно заменять линейными. Закономерность такого подхода обосновал Ляпунов.
Справедливы три теоремы линеаризации.
1.Если линеаризованная система устойчива, то устойчива исходная нелинейная система.
2.Если линеаризованная система неустойчива, то неустойчива исходная нелинейная система.
3.Если линеаризованная система находится на границе устойчивости, то для определения устойчивости исходной нелинейной системы нужно провести дополнительные исследования с целью проверки lim xсв(t)=0.
t
44

3.3. Алгебраический критерий устойчивости
Проверка устойчивости САУ путем вычисления корней характеристического уравнения (3.5) не всегда возможна из-за высокого порядка решаемых уравнений. На практике использует алгебраические и частотные критерии устойчивости.
Критерий Гурвица – алгебраический критерий, он позволяет судить об устойчивости САУ на основе анализа коэффициентов характеристического уравнения (3.5).
Система с характеристическим уравнением (3.5) будет устойчивой, если определитель Гурвица n и все его диагональные миноры n-1., n-2 , … , 1 положительны при а 0 .
Для того, чтобы найти определитель Гурвица, нужно построить матрицу Гурвица.
(3.8)
Матрица Гурвица заполняется по следующему правилу по столбцам относительно главной диагонали. Сначала выписывают коэффициенты на главную диагональ. Ниже главной диагонали записывают коэффициенты с уменьшением индекса, а выше - с увеличением.
Диагональные миноры рассчитываются так
1 =| а1|,
а1 а32= а0 а2 = а1а2 - а3 а0, и т.д.
45
Условием нахождения САУ на границе устойчивости является равенство нулю определителя Гурвица ( n=0), а все
остальные |
диагональные |
миноры |
должны |
быть |
положительными. |
|
|
|
|
Недостатки критерия Гурвица заключаются в |
||||
следующем. |
|
|
|
|
1. Для |
систем при n>5 |
(более |
высокого |
порядка) |
критерии Гурвица требуют анализа очень громоздких выражений, т.е. при n>5 данный критерий практически не используется.
2. Критерий Гурвица не позволяет выделять неустойчивое звено в системе (определить причину неустойчивости САУ).
3.4. Частотные критерии устойчивости САУ
Частотные критерии основаны на изучении связи между формой частотной характеристики САУ и характером распределения корней характеристического уравнения в комплексной плоскости. Наибольшее применение нашли два критерия устойчивости: критерий Михайлова и критерий Найквиста [2].
Критерий устойчивости Михайлова был предложен в 1938 году. Это графический критерий устойчивости, суть которого заключается в следующем.
Если характеристическое уравнение замкнутой САУ
имеет вид |
|
a0 pn + a1 pn-1 + … + an-1 p + an = 0 , |
(3.9) |
то, представив левую часть равенства (3.9) в виде функции
D(p)= a0 pn + a1 pn-1 + … + an-1 p + an 46
и подставив в неѐ p= j , получим уравнение комплексного вектора
D(j )= a0 (j ) n + a1 (j ) n-1 + … + an-1 (j ) + an.
D(j ) задаѐт комплексный вектор, который при изменении угловой частоты колебаний от 0 до опишет на комплексной плоскости некоторую кривую – годограф, или кривую Михайлова.
Для построения кривой Михайлова необходимо в D(j ) выделить действительную и мнимую части:
D(j )= U( )+jV( ),
где
U( ) = a n – a n-2 2 + a n-4 4 - …
V( ) = a n-1 – a n-3 3 + a n-5 5 a - a n-7 7 + …
(n-чѐтное).
Например, при n=8 получим ( с учѐтом j2=-1 )
D(j )= a0 (j ) 8 + a1 (j ) 7 + … + a7(j ) + a8 =
(a0 8 - a2 6 + a4 4 - a2 2+ a8) + j (a7 - a5 3 + a3 5 - a1 7).
Далее, задаваясь различными значениями частоты
= 1, 2,… вычислим координаты точек годографа D(j ): при=0 U( )=a n , V( )=0; при jV( ) .
Рассмотрим случай n=1. D(p)= a0 p + a1 , D(j )=a0 (j )+ a1.
Действительная часть постоянна U( a1
47
jV |
n=1 |
U
0
a1
Рис. 3.8
Рассмотрим случай n=2.
D(p)= a0 p2 + a1p +a2,
D(j )= a0(j )2 + a1(j )+ a2 =[ a2 -a0 2]+j(a1 )
Действительная часть U( =a2 -a0 2.a1 Мнимая часть V( )=a1 .
При =0 V=0, U= a2. При = a2/a0 U= 0, V=a1 a2/a0
Критерий Михайлова формулируется так. Система n-го порядка будет устойчива, если годограф, начинаясь на действительной оси при U , огибает против часовой стрелки начало координат, проходя последовательно ровно n квадрантов (четвертей комплексной плоскости).
Для устойчивых САУ кривая Михайлова всегда имеет плавную спиралевидную форму, уходящую в бесконечность в том квадранте комплексной плоскости, номер которого соответствует степени n характеристического уравнения системы. Более n квадрантов кривая Михайлова для уравнения n-го порядка пройти не может, поэтому неустойчивость САУ всегда связана с нарушением последовательного обхода квадрантов (рис. 3.9).
48
jV
n=3
U
0
an
Кривые Михайлова для неустойчивой системы
Рис. 3.9
Условием нахождения САУ на границе устойчивости является прохождение кривой Михайлова через начало координат.
Для оценки устойчивости замкнутой САУ по известной АФЧХ разомкнутой системы используют критерий, предложенный в 1932 году американским учѐным Найквистом.
При этом исследуемая АФЧХ может быть получена как аналитически, так и экспериментально. Разомкнутая САУ может быть устойчивой, неустойчивой или находиться на границе устойчивости. Если САУ состоит из устойчивых звеньев, то она будет устойчивой в разомкнутом состоянии. При наличии хотя бы одного неустойчивого звена разомкнутая система будет неустойчивой. При наличии в САУ интегрирующего звена система будет находиться на границе устойчивости. Критерий Найквиста формулируется так.
Чтобы замкнутая САУ была устойчивой, необходимо и достаточно выполнение следующих условий: при устойчивой разомкнутой САУ, или находящейся на границе устойчивости, АФЧХ при изменении от до не должна охватывать точку
49
с координатами (-1, j0); при неустойчивой разомкнутой САУ АФЧХ должна охватывать точку (-1, j0) столько раз, сколько корней характеристического уравнения разомкнутой САУ лежит справа от мнимой оси комплексной плоскости.
jV
|
|
=0 |
U |
-1 |
0 |
|
|
Рис. 3.10
Возможно также определение устойчивости САУ по логарифмическим характеристикам.
Будем оценивать устойчивость САУ по амплитудной логарифмической частотной характеристике L( ) и по фазовой характеристике ( ).
Если разомкнутая САУ устойчива, то для устойчивости замкнутой САУ необходимо и достаточно, чтобы во всех областях положительной ЛАХ (L() разность между числом положительных и отрицательных переходов фазовой характеристики () через линию –1800 равнялась нулю.
Введѐм обозначения:
a-точка пересечения L( ) с осью частот; b-точка пересечения () с осью частот;- запас устойчивости по фазе;
l-запас устойчивости по амплитуде.
50
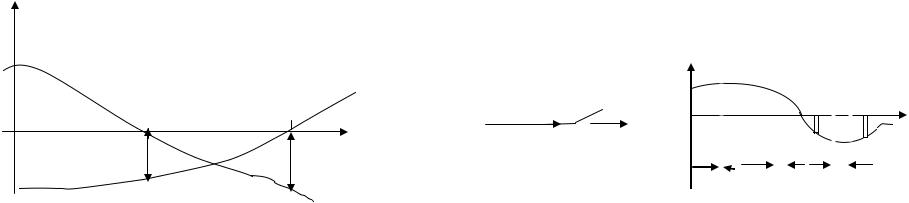
Если точка a расположена левее точки b, в положительной области ЛАХ число переходов () через линию ( )=-180 равно нулю. Система устойчива
L( ),φ(ω) |
|
a |
b |
φ = -180 |
|
|
l |
Рис. 3.11
Если точка b расположена левее точки a, в области положительной ЛАХ есть один переход фазовой характеристики через ось ( )=-180, следовательно, система неустойчива.
4.ЦИФРОВЫЕ СИСТЕМЫ АВТОМАТИКИ
4.1.Определение дискретной системы. Разностные уравнения
Входные и выходные сигналы непрерывных систем являются функциями непрерывного времени t.
Если независимая переменная t принимает только конечное
множество значений |
tK (k 0; 1; 2;...) , то сигнал |
называется дискретным. |
|
51
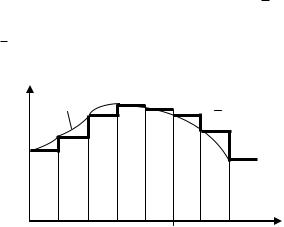
Формирование дискретного сигнала можно представить себе следующим образом (рис.4.1).
|
|
54 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g* t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. |
4.1 |
|
|
|
|
|
|
|
|
|
r |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть имеется ключ Кл (рис. 4.1), который включается на очень короткий промежуток времени . Если на вход такого ключа подать непрерывный сигнал g(t), то на его выходе образуется последовательность импульсов g*(t). Причѐм величена (амплитуда) каждого из импульсов, будет равна амплитуде непрерывного сигнала в дискретные моменты tK . В дальнейшем принимают, что интервал r , (называемый интервалом или шагом дискретизации по времени) является постоянным r =const. Поэтому для интервала наблюдения
Т Н имеем:
ТН К r ;
где К – целое число.
Ключ по существу является импульсным амплитудным модулятором непрерывного сигнала и называется импульсным элементом. Известно, что непрерывные системы описываются дифференциальными уравнениями, а дискретные – разностными уравнениями.
52
Понятие разностного уравнения поясним на следующем примере. Предположим, что нам необходимо вычислить интеграл:
t |
|
y(t) u( ) d |
(4.1) |
0 |
|
Предположим, что подынтегральная функция |
u( ) не |
интегрируемая в замкнутом контуре. Тогда обычный прием интегрирования заключается в том, что функция u(t)
апроксимируется кусочно-постоянной функцией u (t) (рис. 4.2), причѐм
u u r , k r r k r r
u u(
u
0 |
|
|
|
|
|
|
|
r |
2 r |
3 r |
|
|
|
|
|
|
k |
r |
|
||||
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Рис.4.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k r |
k 1 |
|
|
|
|
|
y k r |
u d ru i r |
|
|
(4.2) |
|||
|
|
0 |
i 0 |
|
|
|
|
Формула (4.2) требует запоминания всех прежних значений сигнала u(i r ) для того, чтобы определить значение интеграла в данный момент t k r . Гораздо более простой способ
состоит в том, что вначале находят:
53
|
|
k r r |
k |
|
y k r |
r |
|
u d ru i r , |
(4.3) |
|
|
0 |
i 0 |
|
а затем вычисляют выражение для разности (4.2) и (4.3): |
|
|||
|
y k r |
r |
y k r ru k r |
(4.4) |
или |
y k 1 r |
y k r ru k r |
|
|
|
(4.5) |
|||
Согласно (4.5), |
необходимо запомнить |
только |
||
предыдущее значение интеграла y(K r ) и его значение u( ) в данный момент времени, чтобы определить значение интеграла в последующий момент (К 1) r .
Выражение (4.5) является разностным уравнением 1-го порядка.
Алгоритм его решения заключается в следующем:
1) запоминается начальное условие: y(0)=0 – начальная
сумма;
2) формулу (4.5) применяют последовательно для значений к = 0, 1, 2, …, то есть:
y r ru 0 y 0 ru 0 y 2 r ru r y r
y 3 r ru 2 r y 2 r
…………….
y i r ru i 1 r y i 1 r
На каждом шаге этого итерационного процесса каждое
последующее значение выхода |
y(i r ) вычисляют сложением |
его предыдущего значения |
y (i 1) r c предыдущем |
значением выхода и (i 1) r , умноженным на r . 54
В общем случае линейное разностное уравнение имеет вид:
y(n k) a1 y(n k 1) ... an y(k) |
(4.6) |
|
b0u(n k) b1u(n k 1) ...bnu(k) |
||
|
Для того, чтобы при помощи этой формулы вычислить y(n k) , необходимо запомнить предыдущие значения выхода
y(n k 1), y(n k 2)...y(k) и входа u(n k),u(n k 1)...u(k), а
затем выполнить указанные действия умножения и сложения.
4.2 Методы математического описания дискретных систем
Дискретные системы, также как и непрерывные системы, имеют три формы математического описания во временной области в виде:
-разностных уравнений входа-выхода, являющихся аналоговым дифференциальным уравнением;
-взвешенной временной последовательности, являющейся аналогом описания непрерывных систем при помощи импульсной переходной функции;
-разностных уравнений в переменных состояниях, являющихся аналогом описания дифференциальных уравнений в переменных состояниях для непрерывных систем
[3].
1) Разностные уравнения вход-выход.
Понятие разностного уравнения введено ранее (см. уравнение (4.6)). При этом его приводят к виду:
y(k) b0u(k) b1u(k 1) ... bnu(k n) |
(4.7) |
|
a1 y(k 1) a2 y(k 2) ... anu(k n) |
||
|
Число y(k) характеризует выход в момент К r (шаг дискретности r обычно опускают). Числа y(к-1), y(к-2)
характеризуют вход в дискретные моменты к, к-1,…и так
55
далее (они также хранятся в памяти). Уравнение (1.7) называют рекурсивным, или разностным, позволяющим вычислить каждое последующее значение выхода по предыдущим данным.
2)Описание линейной системы при помощи взвешенной
временной последовательности. |
|
||
Для |
систем, |
описываемых |
линейными |
дифференциальными уравнениями, очень важным и удобным является понятие импульсной переходной функции (ИПФ).
ИПФ для непрерывной системы определяют как еѐ реакцию на дельта-функцию. Она имеет вид некоторой непрерывной функции.
В дискретных системах в случае входного воздействия в виде дельта-функции получается последовательность чисел, а не непрерывная функция времени. Рассмотрим систему, описываемую разностным уравнением (4.7), находившуюся в состоянии покоя до момента приложения входного воздействия, то есть y(k)=0 при k = -1, -2; …
Пусть:
|
|
u k 0 k |
1, k 0 |
(4.8) |
|
|
|
0, k 0 |
|||
|
|
|
|
||
где 0 (k ) |
- дельта-последовательность. |
|
|||
Положив |
в |
уравнении (4.7) |
uK 0 (k ) и обозначив |
||
получающуюся реакцию через h(k), можно записать: |
|
||||
h(k) b (k) b (k 1) ... b (k n) |
|
||||
|
0 |
1 |
n |
(4.9) |
|
a1h(k |
1) a2h(k 2) ... anh(k n). |
||||
|
|||||
Взвешенную временную последовательность h(k) называют весовой. Вычисление h(k) по уравнению (4.9) проведѐм следующим образом. Полагая, что h(k) = 0, k < 0, получим:
56
h(0) b0 |
|
|
|
|
|
|
|
|
|
h(1) b1 (0) a1h(0) b1 a1b |
|
|
|
|
|
|
(4.10) |
||
h(2) b (0) a h(1) a h 0 b a b a2b |
a b |
||||||||
2 |
1 |
2 |
2 |
1 |
1 |
1 |
0 |
2 |
0 |
Рассмотрим теперь общий случай, когда входная функция представляет собой сумму -последовательностей, приложенных в моменты k=0, 1, 2, …, то есть:
u k |
0, k 0 |
|
|
|
л , k 0 |
|
|
||
|
|
|
|
|
или |
k 1 1 k 2 2 |
k ... |
|
|
uk 0 0 |
(4.11) |
|||
Тогда на основании принципа суперпозиции регулируемая переменная системы будет равна сумме реакций, вызванных сигналами: u(0), u(1),…,u(k):
|
|
q |
|
y k y 0 k y ' k ... y 2 |
k y j k |
|
|
j 0 |
|
q |
|
или |
y k j h k j |
(4.12) |
|
j 0 |
|
Таким образом, если на вход системы, находящейся в покое, подана временная последовательность чисел – u(0), u(1),…, то временная последовательность на выходе:
q |
|
|
y k h k j ..и.. j . |
к 0,1,2,... (4.13) |
|
j 0 |
|
|
После замены переменной m = k-j |
|
|
q |
|
|
y k h m ..и.. k m |
(4.14) |
|
m 0 |
|
|
Выражения (1.13) и (1.14) являются аналогами интеграла свѐртки для непрерывных систем.
57
3)Описание линейной системы при помощи разностных уравнений в переменных системах.
Аналогично тому как при описании непрерывных систем используются дифференциальные уравнения 1-го порядка переменных состояния, для дискретных систем используются разностные уравнения 1-го порядка:
x k 1 r Ad k r x k r Bd k r u r
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
k |
|
k |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
y |
Cd |
x |
|
|
|
|
|
|
|
(4.15) |
|||||||||||||||||
или, учитывая, что r const |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
k 1 |
|
k |
|
k |
|
k |
|
k |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x |
Ad |
x |
Bd |
u |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
k |
|
k |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
y |
Cd |
x |
|
|
|
|
|
|
|
(4.16) |
|||||||||||||||||
Здесь |
|
Ad(k), |
|
|
Bd(k), Сd(k) –матрицы |
|
размерности |
|||||||||||||||||||||||||||||
n n; |
n m; |
p n соответственно. |
|
|
|
|||||||||||||||||||||||||||||||
|
|
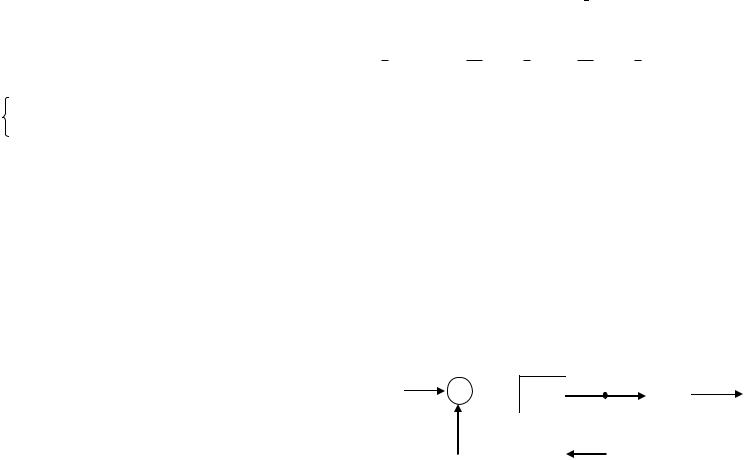
Структурная схема дискретной системы, описываемой |
||||||||||||||||||||||||||||||||||
уравнениям (4.16), приведена на рис. 4. 3. |
|
|
|
|||||||||||||||||||||||||||||||||
u(k) |
|
|
|
|
|
|
|
|
|
|
|
|
x(k+1) |
|
|
|
x(k) |
|
|
|
y(k) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
||||||||||||||||||||||
|
Bd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЭЗ |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.4.3
58
