Учебное пособие 800222

нулевых начальных условиях, то символ р можно рассматривать как число.

Основной характеристикой каждого ЛДЗ является его передаточная функция, которую принято обозначать K(p) или

W(p).

W(p) находится из дифференциального уравнения звена (2.1) при нулевых начальных условиях как отношение изображения по Лапласу выходного и входного сигналов

Зная передаточную функцию звена, можно найти значение выходного параметра по значению входного параметра

Для оценки динамических свойств звеньев используют временные и частотные характеристики.

2.2. Временные и частотные характеристики

Временные характеристики h(t) и g(t) называют переходной характеристикой и импульсной переходной характеристикой соответственно

Переходная характеристика h(t) – определяет реакцию звена на входной сигнал 1(t):

где L -1 - обратное преобразование Лапласа.

Другой важной характеристикой динамического звена является частотная характеристика. При подаче на вход звена

где А- амплитуда воздействия, а - его угловая частота, на выходе звена в установившемся режиме будет получена также гармоническая функция

отличающаяся от входного воздействия и по амплитуде и по фазе. Представим входную и выходную гармонические функции в экспоненциальном виде

х вх= Авх ej t

(2.8)

x вых= Авых· ej t+ ,

ачастотную передаточную функцию получим, подставляя в

где A( ) – амплитуда (модуль частотной передаточной функции)

Для наглядного представления частотных свойств динамических звеньев используют частотные характеристики.

1. Амплитудно-частотная характеристика (АЧХ) определяет зависимость амплитуды выходного сигнала от частоты колебаний при постоянной амплитуде входного сигнала (рис.

2.1).

Рис. 2.1

3. Фазовая частотная характеристика (ФЧХ) показывает фазовые сдвиги, вносимые звеном на разных частотах (рис. 2.2).

21

(АФЧХ, или годограф) объединяет АЧХ и ФЧХ при использовании их в качестве полярных координат (рис. 2.3).

Рис. 2.3

22

4. Иногда целесообразно использовать вещественную и мнимую частотные характеристики P( ) и Q( ) из формулы

(2.9).

Связь между перечисленными частотными характеристиками определяется формулами (2.11) и (2.12), а также соотношениями

5.Наиболее удобными в использовании являются логарифмические частотные характеристики ЛАХ и ЛФХ.

Прологарифмируем выражение частотной передаточной функции (2.9).

Величину lnA(w) называют логарифмической амплитудной частотной характеристикой (ЛАХ), а ( ) - логарифмической фазовой частотной характеристикой (ЛФХ).

Для построения ЛАХ используют формулу

Величина L( ) выражается в децибелах. Децибел – это 0,1 бела, а бел – логарифмическая единица, которая соответствует десятикратному увеличению мощности (1 бел – в 10 раз, 2 бела – в 100 раз, 3 бела - в1000 раз).

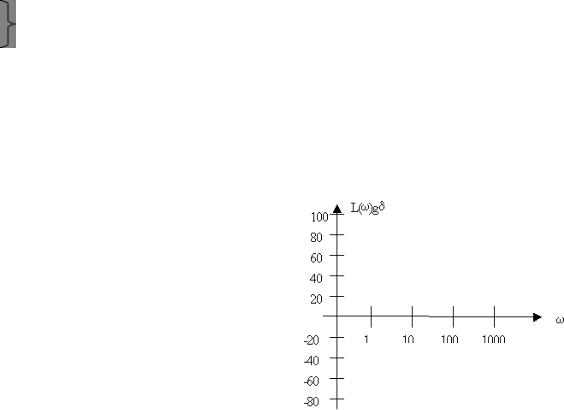
ЛАХ строится в логарифмическом масштабе частот в стандартной логарифмической сетке (рис. 2.5).

23

По оси абсцисс откладывается угловая частота в логарифмическом масштабе, при этом отрезки оси, соответствующие изменению частоты в одинаковое число раз оказываются равными.

Интервал частот , отличающихся друг от друга в 10 друг от друга в 10 раз, называют декадой и обычно принимают за единицу логарифмического масштаба частот масштаба частот.

Ось ординат может пересекать ось абсцисс в произвольном месте. Обычно располагают вертикальную ось так, чтобы с права от нее находился диапазон частот, существенных для данного устройства.

Главное достоинство логарифмического метода – это возможность построения частотных характеристик непосредственно по виду передаточной функции.

Кроме того, использование логарифмического масштаба позволяет охватить большой диапазон частот.

ЛАХ строится в координатной сетке, изображѐнной на рис. 2.4.

.

Рис. 2.4

24

ЛФХ строится в координатной сетке, аналогичной изображѐнной на рис. 2.4, а на оси ординат ( град) принято выделять значения 0, ±45, ± 90, ±135, ± 180, ±225 град.

Рекомендуется совмещать две координатные сетки так, чтобы ось L(w)=0 ЛАХ совпадала с осью =-180 ЛФХ.

2.3 Основные типы ЛДЗ

Безынерционное звено описывается дифферен-

где k – коэффициент передачи (коэффициент усиления) звена. Передаточная функция этого звена постоянна

К безынерционным звеньям можно отнести делитель напряжения, а также электронный или полупроводниковый усилитель с пренебрежимо малой постоянной времени (звено мгновенно, без инерции, реагирует на подаваемый на вход единичный ступенчатый сигнал).

Переходная функция безынерционного звена h(t)=1(t) ступенчатая функция (рис. 2.5). Величина скачка равна k.

Рис. 2.5

25

Частотная передаточная функция безынерционного звена имеет вид

(фазовые сдвиги отсутствуют, ЛФХ совпадает с осью частот и может не учитываться при расчѐтах).

ЛАХ безынерционного звена имеет вид

Рис. 2.6

Апериодическое звено (инерционное) описывается

Примерами таких звеньев могут быть RC и RL цепи

Рис.2.7

Переходная функция h(t) имеет вид:

Рис. 2.8

Для построения ЛАХ и ЛФХ апериодического звена найдѐм частотную передаточную функцию звена

L( )=20lgА() = . (2.27)

График ЛАХ апериодического звена строим приближѐнно. Находим сопрягающую частоту =1Т и наносим еѐ на логарифмическую сетку.

При малых частотах <1/T, T<1 и 2 T2. Следовательно, 1+ 2 T2 1 и можно считать, что L( )=20lgk.

апериодического звена ( )= - arctg( T).

Таким образом, при <1/T график ЛАХ представляет собой прямую, параллельную оси частот, а при >1/Т график

Рис. 2.9 28

Колебательное звено описывается дифференциальным уравнением

Примером колебательного звеньев может быть RLС цепь, изображѐнная на рис. 2.10.

Рис. 2.10

Переходная функция колебательного звена имеет вид

h(t)=k

(2.30)

и еѐ график приведѐн на рис. 2.11. 29

Таким образом, можно приближенно считать, что ЛАХ колебательного звена представлят собой ломаную линию ABCD, состоящую из трѐх прямолинейных участков на отрезке АВ это прямая, параллельная оси частот, на отрезке СD это прямая, имеющая угол наклона -40 дБ на декаду (рис. 2.12). Такую ломаную ЛАХ можно использовать при параметре затухания 0,5<c<1,2. При других значениях с реальная ЛАХ будет сильно отклоняться от ломаной и пользоваться данным упрощением нельзя.

30

К интегрирующим звеньям можно отнести RC цепь

Рис. 2.13

Переходная функция интегрирующего звена имеет вид

еѐ график приведѐн на рис. 2.14.

ЛФХ имеет вид ( )=-90 . Графики ЛАХ и ЛФХ интегрирующего звена приведены на рис. 2.15.

Рис. 2.15

Дифференцирующее звено описывается уравнением

Передаточная функция идеального дифференцирующего звена имеет вид

На практике дифференцирующие звенья применяются в САУ для коррекции и в большинстве случаев реальные

33

дифференцирующие звенья имеют передаточные функции

Рис. 2.16

Легко видеть, сто реальное дифференцирующее звено представляет собой два последовательно включенных в цепь звена - идеальное дифференцирующее и апериодическое.

Переходная функция реального дифференцирующего звена

Т

График переходной функции приведѐн на рис. 2.17.

Рис. 2.17

34

При малых частотах ( <1/T , 2 T2) L( )20 lg k

(прямая с положительным углом наклона, АВ на рис. 2.18).

дифференцирующего звена, отличающаяся от действительной ЛАХ в точке излома на величину не более 3 дБ.

Рис. 2.18 35

Из рассмотренных типовых звеньев элементарными являются безынерционное, интегрирующее и дифференцирующие. Все остальные звенья можно получить из элементарных звеньев, соединяя их между собой определенным образом. Звенья, у которых переходная функция своевременно стабилизируется, называются устойчивыми (они описываются линейными дифференциальными уравнениями (ЛДУ) с положительными коэффициентами). Типовые звенья всегда устойчивы (кроме интегрирующего звена, которое называется нейтральным). В неустойчивых звеньях переходный процесс является расходящимся, и такие звенья описываются ЛДУ с отрицательными коэффициентами. Для устойчивых и неустойчивых звеньев одного типа амплитудные характеристики одинаковы, а фазовые различны. Сдвиг фазы в устойчивом звене меньше, чем в неустойчивом.

2.4. Способы соединения звеньев САУ

При исследовании САУ можно разбить систему на комбинацию динамических звеньев с известными передаточными функциями. Будем считать динамические звенья направленными и независимыми, т.е. такими, сигналы которых проходят от входа к выходу, а подключение последующих звеньев не влияет на характер переходных и установившихся процессов предыдущих звеньев. В САУ существует три способа соединения звеньев: последовательное, параллельное и с обратной связью (ОС).

36

Рис. 2.19

Последовательное соединение изображено на рис. 2.19. При последовательном соединении звеньев выходной сигнал предыдущего звена является входным сигналом для последующего звена, а результирующая передаточная функция равна произведению передаточных функций отдельных звеньев.

W(р)=W1(р)W2(р)*...*Wn(P)=

. (2.27)

При параллельном соединении (рис. 2.20) на вход всех звеньев подается общий сигнал, а на выходе образуется сигнал, являющийся суммой выходных сигналов звеньев.

Рис. 2.20

Результирующая передаточная функция является суммой передаточных функций звеньев.

W(р)=W1(р)+W2(р)+...+Wn(P)=

(2.28)

37

При соединении с ОС выходной сигнал первого звена является входным для второго, причем входной сигнал первого звена образуется в результате сложения или вычитания входного сигнала и выходного сигнала второго звена.

где знак минус в (2.29) ставится при положительной обратной связи, а плюс - при отрицательной обратной связи.

Если второе звено в цепи обратной связи отсутствует, то

Таким образом, имея структурную схему САУ и зная передаточные функции звеньев, можно найти передаточную функцию САУ и проводить с еѐ помощью исследование САУ на точность, быстродействие и устойчивость.

38