Учебное пособие 800120

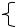
лучевых трубках (ЭЛТ) телевизоров и блоков питания, полей в конденсаторах или системе монтажных проводников печатных плат, образующих паразитные емкости. Задачи анализа тепловых полей в конструкциях РЭС формируются как задачи распределения температуры в толще корпуса конструкции с учетом наличия теплонагруженных элементов и температуры окружающей среды, а одной из основных проблем анализа механических полей является задача анализа механических колебаний при вибрационных нагрузках и механической прочности

дифференциальной краевой задачи (ДКЗ) следующим образом.

где L - дифференциальный оператор, u = u(X, t) - функция потенциала (неизвестная функция - решение ДКЗ, характеризующая исследуемое поле: например, в случае электростатического поля это разность потенциалов, для магнитного поля - векторный потенциал, для теплового поля - температура и т.п.), f = f(X, t) - заданная функция, характеризующая воздействие внешних факторов, X - набор параметров, характеризующих размерность ДКЗ или пространственные координаты (в одномерном случае X = x (стержень), в двумерном X = (x, y) (плоская конструкция), в трехмерном - X = (x, y, z) (объемная конструкция)), X ( - область определения ДКЗ, соответствующая конфигурации исследуемой конструкции), t - временной фактор, t t0, ), t0 - время начала моделирования.

Граничные условия задают на границе конструкции или ее отдельных участках:

39

где Г - граница области определения ДКЗ (Г = ), =(t) - заданная функция, характеризующая распределение поля на границе конструкции.

В начальный момент времени моделирования t0 задаются начальные условия

где = (Х) - заданная функция, характеризующая состояние поля в начальный момент времени t = t0.

Дифференциальная краевая задача (3.2) - (3.4) является нестационарной (то есть учитывает изменения параметров поля во времени). В стационарном случае (u u(t)) ДКЗ

и не содержит начальных условий. Начальные и граничные условия ДКЗ принято называть краевыми условиями.

Математические модели полей в конструкциях РЭС в виде ДКЗ получают с помощью наиболее общих физических законов, описывающих исследуемые процессы в конструкции РЭС (например, законов сохранения энергии - уравнения Максвелла, Фурье и т.п.). Таким образом, задачи анализа полей относятся к математическим моделям микроуровня, обеспечивающим наиболее полное и точное описание реальных физических процессов в конструкциях РЭС [5].

Решить задачу анализа поля (3.5) значит найти функцию потенциала поля u, удовлетворяющую дифференциальному уравнению и краевым условиям. Аналитическое решение данной задачи представляет собой

40

сложную проблему, прежде всего из-за конфигурации области определения (наличие разнообразных вырезов и отверстий ПП), а также в силу того, что граничные условия, как правило, задаются на отдельных участках границы или даже на фрагментах внутренней области конструкции (например, для расчета теплового поля такие участки соответствуют местоположению теплонагруженных элементов). В таком случае даже при простейшем дифференциальном уравнении нахождение аналитического (в виде явной функциональной зависимости) решения ДКЗ не представляется возможным. Поэтому на практике используют численные методы анализа полей в конструкциях РЭС - метод конечных разностей и метод конечных элементов.

3.2.2. Метод конечных разностей Основная идея метода конечных разностей

заключается в переходе от решения дифференциальной краевой задачи (3.5) (для упрощения расчетов ограничимся рассмотрением стационарной задачи) к решению системы линейных алгебраических уравнений.

При этом решение u = u(x) находится только в отдельных точках конструкции (узлах разностной сетки), а не в любой точке x как в случае аналитического решения

[6].

Вметоде конечных разностей используются приближенные формулы конечных разностей, позволяющие перейти от частных производных к их разностным аналогам (данные формулы получают на основе разложения функции u(x) решения ДКЗ в ряд Тейлора).

Водномерном случае (u = u(x) ) используются следующие формулы конечных разностей.

Для производной первого порядка можно использовать одну из трех формул.

41

1. Формула левой производной

(3.6)

получила свое название из-за того, что использует значение функции u в точке x и в точке x-h, находящейся слева от нее. 2. Формула правой производной имеет вид

единственная формула конечно-разностной аппроксимации

В формулах (3.6) - (3.9) используется знак " " - приблизительно равно, поэтому важно знать погрешность каждой такой аппроксимирующей замены. Для оценки ошибки каждой из формул (3.6) - (3.9) используем разложение функции u(x) в ряд Тейлора:

. (3.10)

Перенесем u(x) в левую часть уравнения (4.10) и разделим обе его части на h:

(3.11)

или

42

где 0(h) - величина того же порядка, что и h, 0(h)=const h. Таким образом, погрешность формулы правой производнойравна 0(h). Такую же погрешность имеют формулы левой и центральной производных.

Формулу конечных разностей для производной второго порядка легко получить, используя формулы первых производных

,

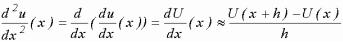где

.

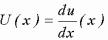погрешность формулы (3.9) составляет 0(h2), то есть величину того же порядка, что и h2.

Аналогичным образом можно получить формулы конечно-разностной аппроксимации для производных третьего, четвертого и более высоких порядков.

В двумерном случае (u = u(x, y) ) формулы конечных разностей записываются следующим образом. Формулы

Рассмотрим алгоритм метода конечных разностей решения ДКЗ (3.5).

1.Исходя из требуемой точности выбираем шаг разбиения (шаг разностной сетки) h.

2.Строим в области определения ДКЗ разностную сетку (то есть покрываем конструкцию РЭС точками - узлами прямоугольной сетки) с выбранным шагом.

3.В каждом из граничных узлов сетки записываем граничные условия задачи (3.5), и если граничные условия содержат производные, то применяем к ним формулы конечных разностей.

4.В каждом из внутренних узлов разбиения записываем дифференциальное уравнение задачи (3.5) и заменяем производные по формулам конечных разностей.

5.Полученную систему линейных алгебраических уравнений (СЛАУ), в которой неизвестными являются значения функции u(x) в узлах сетки, решают на ЭВМ с применением методов численного решения СЛАУ (чаще всего благодаря специальному, трехдиагональному виду матрицы СЛАУ используют метод прогонки) [7].

Рассмотрим этапы описанного алгоритма для решения одномерной задачи:

d х2

u(1) = 2, u(2) = 3 .

44

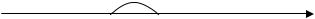
1. Требуемая точность решения задачи ε ≤ 0,04. Так как в уравнении (3.18) содержится только производная второго порядка, то ошибка метода определяется погрешностью формулы производной второго порядка ε = 0(h2), то есть ε h2, или h √ε, поэтому выбираем h √ε, например h = 0,2.

Рис. 3.1

3. Граничными узлами построенной сетки являются точки x1 и x6, запишем в них граничные условия задачи

(4.18):

u(x1) = 2, u(x6) = 3,

таким образом, получены два линейных уравнения в граничных узлах разностной сетки.

4. Внутренними узлами сетки являются точки x2, x3, x4, x5. В каждом из них запишем дифференциальное уравнение задачи (3.18). Получим

d 2u(х2) = х2 2 = 1,44,

d х2

d 2u(х3) = х3 2 = 1,96,

d х2

45

d 2u(х4) = х4 2 = 2,56,

d х2

Применяя формулу вторых производных с шагом h = 0,2 получим

u(х3 )-2 u(х2)+ u(х1)= 1,44∙(0,2)2, u(х4 )-2 u(х3)+ u(х2)= 1,96∙(0,2)2, u(х5 )-2 u(х4)+ u(х3)= 2,56∙(0,2)2, u(х6 )-2 u(х5)+ u(х4)=3,24∙(0,2)2,

таким образом, получены еще четыре линейных уравнения во внутренних узлах разностной сетки..

5. Записывая вместе уравнения во внутренних и граничных узлах, получим систему шести уравнений

(разностная схема ДКЗ (3.18)).

Каждая разностная схема характеризуется своим шаблоном, то есть изображением соседних узлов сетки, входящих в разностное уравнение. Для одной и той же задачи можно несколько разностных схем в зависимости

46

от того, какие из формул конечных разностей для первой производной использовать.

Решая систему ЛАУ на ЭВМ найдем значения решения в узлах сетки, притом решение будет найдено с требуемой точностью.

Несомненным преимуществом метода конечных разностей является гарантированная точность получаемых решений, а к недостаткам метода следует отнести невозможность получения решения в любой точке конструкции.

3.2.3. Метод конечных элементов

Метод конечных элементов, в отличие от метода конечных разностей, позволяет получить решение в аналитическом виде, но не позволяет провести количественной оценки точности полученного решения [8].

Основная идея метода конечных элементов заключается в разложении искомого решения ДКЗ (неизвестной функции u(x) по базисным функциям S1(x),...,

где i - коэффициенты разложения, которые требуется найти. Такое разложение можно рассматривать как аналогию разложения произвольного вектора в векторном пространстве R3 по единичным ортам (базисным векторам) , то есть так же как в векторном пространстве любой вектор можно представить в виде линейной комбинации базисных векторов, так в функциональном пространстве любую функцию можно представить в виде (3.19).

Рассмотрим основные этапы метода конечных элементов.

1. Разбиваем конструкцию РЭС или ее отдельный участок на конечные элементы (в одномерном случае при

u = u(x) конечный элемент – это отрезок, в двумерном случае u = u(x, y) - треугольник, в трехмерном - пирамида или куб).

Полученные конечные элементы объединяют в "ансамбль", то есть вводят сквозную нумерацию для вершин всех конечных элементов.

Обозначим N общее число вершин конечных элементов.

В результате получаем сеточное разбиение исследуемой области.

2. В каждом из узлов конечных элементов (узлов сетки) построим базисную функцию.

Базисная функция Si(x), i = - это полином (обычно первой степени, то есть линейная функция), обладающая следующим свойством: базисная функция Si(x) равна 1 только в i-ом узле сетки, а в остальных узлах равна 0 (для ясности и простоты изложения ограничимся рассмотрением одномерного случая):

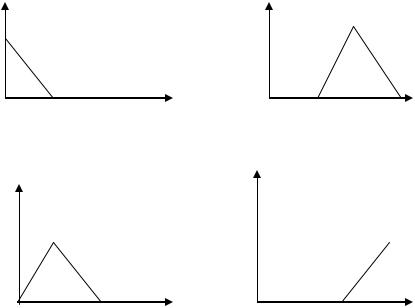
В качестве примера рассмотрим отрезок [0, 3], выбрав шаг сетки h = 1, тогда N = 4 (три конечных элемента, четыре вершины).

Разбиение отрезка и графики базисных функций приведены на рис. 3.2.

48

Рис. 3.2

Из определения базисной функции с учетом того, что Si(x) - полином первого порядка (Si(x) = ax+b) легко найти базисные функции:

-х+1, х[0, 1] S1(x) = 0, х[1, 3],

х, х[0, 1] S2(x) = -х+2, х[1, 2] 0, х[2, 3],

0, х[0, 1] S3(x) = х-1, х[1, 2]

-х+3,х [2, 3],

49

0, х[0, 2] S4(x) = х-2, х[2, 3] .

3. Требуется найти коэффициенты разложения (3.19)1, ..., N (базисные функции S1(x), ..., SN(x) к данному моменту уже известны, в нашем примере N=4).

Для этого выпишем дифференциальное уравнение краевой задачи, умножим обе его части на произвольную функцию U(x) и проинтегрируем обе части уравнения по области определения (в одномерном случае = [a, b])):

Затем подставим в уравнение (3.20) вместо u(x) разложение (3.19), а в качестве U(x) выберем первую из базисных функций (U(x)=S1(x) ):

где Si(x), i = 1,…,N- известные линейные функции, f(x) - заданная правая часть ДКЗ, i - неизвестные коэффициенты (константы), следовательно, под знаком интеграла стоят полиномы не выше второго порядка, вычисление интегралов в таком случае не представляет серьезной проблемы, причем в ходе вычислений учитываются граничные условия. В результате вычисления интегралов в

50

формуле (3.21) получим первое линейное уравнение относительно неизвестных коэффициентов 1, 2, ..., N.

Чтобы получить второе уравнение, в (3.20) подставим U= S2(x) и проведем интегрирование, и т.д.

Для получения последнего уравнения в (3.20) подставляем U= SN(x). Таким образом, получена система из N линейных уравнений относительно N неизвестных (коэффициентов 1, 2, ..., N). Решив полученную систему на ЭВМ и подставив найденные значения i, i =1,…,N в формулу (3.19) получим искомое решение u(x)

ДКЗ (3.5).

Внашем примере необходимо найти коэффициенты

1, 2, 3, 4 разложения

u(x) = 1 S1(x) + 2 S2(x) + 3 S3(x) + 4 S4(x) (3.22)

решения следующей полевой задачи.

Провести анализ теплового поля в одномерном стержне длины l =3; к левому концу стержня подводится тепловой поток интенсивности q, а правый конец стержня теплоизолирован (коэффициент теплопроводности стержня x):

d 2u(х) = 0, х (0,l), l=3,

d х2

d u(3) = 0. d х

Для данной задачи разбиение отрезка [0, 3] с шагом h =1 и базисные функции S1(x), S2(x), S3(x), S4(x) приведены в пункте 2 данного алгоритма. Подставим выражения, полученные для базисных функций, в формулу (3.22):

51

Умножая обе части дифференциального уравнения ДКЗ (3.23) последовательно на каждую из базисных функций S1(x), S2(x), S3(x), S4(x) , интегрируя их по области определения (х [0, 3]) получим четыре интегродифференциальных уравнения. Вычислив интегралы с применением формулы интегрирования по частям, получим систему уравнений для нахождения коэффициентов 1, 2,

3, 4:

1 - 2 = q/ x,

2– 2 3 + 4 =0,

3 - 4:=0

Полученную систему линейных алгебраических уравнений решают на ЭВ/М, так как на практике целесообразно для достижения хорошей точности решения выбирать возможно меньший шаг разбиения h, и получаемые в методе конечных элементов системы имеют большую размерность.

Вопросы для самопроверки

1.Приведите пример непрерывной и дискретной модели технического устройства.

2.Приведите примеры математических моделей различных уровней иерархии.

3.Охарактеризуйте математическую постановку полевых задач.

4.Почему на практике применяют численные методы анализа полей в конструкциях РЭС?

5. Постройте базисные функции Si(x,y) = ai x + bi y + ci, z в

52

узлах конечного элемента - треугольника с вершинами в точках с координатами (1, 3), (2, 1), (3, 2).

6 Получите третье и четвертое уравнения системы линейных алгебраических уравнений относительно коэффициентов 1, 2, 3, 4 в разложении (3.22).

7. Проведите сравнительный анализ численных методов анализа полей и дайте рекомендации по практическому применению каждого из них.

4.ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ В

Оптимальное проектирование – это процесс принятия наилучших (оптимальных в некотором смысле) решений с помощью ЭВМ. Данная проблема возникает и требует решения на всех этапах проектирования и во многом определяет технико-экономическую эффективность и технологичность проектируемых изделий.

Большинство задач принятия решений можно сформулировать в терминах теории математического программирования, то есть в виде совокупности критериев качества и ограничений.

В соответствии с общепринятыми обозначениями выделим управляемые (внутренние) параметры объекта проектирования X=(x1, x2.,…,xn) и выходные параметры

Y=( y1,y2.,…,ym).

Как правило, при оптимизации целесообразно изменять не все внутренние параметры, а только те из них, которые оказывают наиболее существенное влияние на выходные параметры. Выбор управляемых параметров

чувствительности, либо в интерактивном режиме по желанию проектировщика [2] .

Известна математическая модель объекта проектирования, задающая зависимость выходных параметров Y от управляемых параметров X , адекватно описывающая работу объекта проектирования:

где вектор F=(f1,f2.,…,fm) в качестве компонент может включать как функциональные, так и алгоритмические зависимости. В скалярном виде формула (3.17) примет вид:

Оптимизационная задача не может быть сформулирована при отсутствии математической модели объекта проектирования, при этом вид математической модели во многом определяет целесообразность и возможность применения того или иного метода .

На каждом этапе проектирования конструкции или технологии РЭС в начале работы приходится принимать решения в условиях неопределенности. Чаще всего это относится к построению или выбору варианта структуры проектируемого иерархического блока (модуля) объекта проектирования при нисходящем проектировании в рамках блочно-иерархического подхода [3], то есть к задачам структурной оптимизации.

Выбор варианта структуры во многом снимает неопределeнность, что позволяет строить математическуюмодель (4.1), (4.2) и проводить на ее основе

54

параметрическую оптимизацию, то есть подбор наилучшего набора значений управляемых параметров, при которых выполняются ограничения (технические требования технического задания) и достигают своих экстремальных значений (максимума или минимума) критерии качества объекта проектирования (наиболее важные с точки зрения проектировщика выходные параметры объекта проектирования, по которым оценивается его качество).

4.2. Постановка задачи параметрической оптимизации на основе анализа требований ТЗ

Критерии качества и ограничения задачи параметрической оптимизации прямо либо опосредованно зависят от выходных параметров объекта проектирования

Y=(y1,y2.,…,ym).

В простейшем случае в качестве критериев качества могут быть выбраны наиболее существенные с точки зрения проектировщика выходные параметры. Все остальные выходные параметры при этом необходимо учесть в виде ограничений. Критерии качества в литературе принято называть также целевыми функциями, критериями оптимальности, частными критериями качества, функциями цели и т.п..

Обозначим критерии качества Ki=Ki(x1,x2.,…,xn), i=1,…,s, где s – количество критериев качества, а Ki(X) – либо один из выходных параметров Y=(y1,y2.,…,ym), либо Ki(X)=f(X), где зависимость f(X) задана.

Все ограничения задачи параметрической оптимизации получаем на основе анализа технических требований к параметрам объекта проектирования, содержащихся в ТЗ. Рассмотрим формализацию ограничений на примере выходных параметров Y ( для внутренних параметров Х справедливы аналогичные рассуждения ).

55

Технические требования имеют вид yj = TTj + j, где TTj – желаемое значение параметра yj, а j – его допустимый разброс ( j=1,…,m ).

Математическая постановка задачи параметрической оптимизации как задачи математического программирования имеет вид

Ki=Ki(X) extr,

gl(X) , (4.3) i=1,…,s,

l=1,…,L.

Рассмотрим в качестве примера типичное ТЗ на разработку непрерывного объекта – ТЗ на разработку принципиальной схемы электронного усилителя: ”Коэффициент усиления Кo на средних частотах должен быть быть не менее 10000, входное сопротивление Rвх не менее 1 МОм, выходное сопротивление Rвых не более 200 МОм, верхняя граничная частота fв не менее 100 кГц, температурный дрейф нуля Uдр не более 50 мКв/град; усилитель должен нормально функционировать в диапазоне температур от –50 до +60 градусов Цельсия, напряжения источников притания +5 и – 5 В, предельные отклонения напряжений не более +0,5%, усилитель эксплуатируется в стационарной установке, монтаж выполнять на печатной плате 60х40 мм”. В данном случае выходными параметрами являются Y={ Кo,Rвх, Rвых, fв, Uдр }. К внешним воздействиям относятся температура окружающей среды и напряжения источников питания. Управляемыми параметрами являются параметры элементов схемы Особенность технического задания для дискретных объектов заключается в форме записи ограничений (условий работоспособности), которые могут иметь вид логических уравнений, таблиц истинности или даже текстовую форму.

56

Целью решения задачи параметрической оптимизации (3.19) является определение такого набора значений параметров X*=(x1*, x2*.,…,xn*), X* ХР, при котором критерии качества Ki(X*), i=1,…,s достигают своих наилучших (минимальных или максимальных ) значений.

4.3. Классификация задач параметрической оптимизации

Задача параметрической оптимизации (4.3) является многопараметрической, многокритериальной и содержит ограничения, все эти факторы определяют проблемы, возникающие в процессе ее решения. В зависимости от вида критериев качества и ограничений, проводят классификацию задач параметрической оптимизации (задач математического программирования). Если целевая функция и ограничения линейные функции вида С0 + С1Х1+ С2Х2+…+ СnХn., то задача оптимизации называется задачей линейного программирования, в противном случае – задачей нелинейного программирования.

Если целевая функция квадратичная, а ограничения – линейные функции, то задача (4.3) называется задачей квадратичного программирования.

Если целевая функция и ограничения имеют произведения Х1 Х2 … Хn, то задачу (4.3) называют задачей геометрического программирования.

Если целевую функцию можно представить в виде суперпозиции функций f1 (f2 (f3 …( fk (Х))…)) , то задача (4.3) – это задача динамического программирования.

Если целевая функция и ограничения целочисленные функции то задача (4.3) – это задача целочисленного программирования Кроме того, в зависимости от вида

оптимизации может быть детерминированной или стохастической, непрерывной или дискретной, аналитической или алгоритмической, при этом для каждого класса задач имеется свой, в достаточной степени апробированный, математический аппарат. Так, для задач линейного программирования успешно применяется симплекс-метод [ 4 ].

Характерной особенностью задач оптимизации в САПР является тот факт, что классические методы нахождения экстремума практически неприменимы, так как в большинстве случаев используются алгоритмические модели. В связи с этим вычисление значений критериев качества и их производных производится численными методами. Поэтому наиболее универсальными и эффективными для задач нелинейного программирования являются методы поисковой оптимизации.

Для обеспечения возможности применения методов поиска к решению задачи оптимизации в постановке (4.3) необходимо некоторым образом упростить математическую постановку задачи: перейти от многокритериальной задачи оптимизации к однокритериальной и от задачи с ограничениями - к задаче безусловной оптимизации.

4Методы.4. перехода от многокритериальной задачи оптимизации к однокритериальной

Для того, чтобы оценить, насколько хорошо удовлетворяют требованиям ТЗ значения частных критериев качества при заданном наборе значений внутренних параметров X=(x1, x2.,…,xn), нужно построить обобщенный критерий качества (обобщенную целевую функцию) f(Х), которая одновременно учитывает требования ко всем частным критериям.

58