Задачи для самостоятельного решения

1. По соленоиду длиной без сердечника,

имеющему витков течёт ток . Определить циркуляцию вектора магнитной индукции вдоль контура, изображённого на рис. 3.6 (а, б).

Ответ: а) ; б) .

2. Вычислить циркуляцию вектора индукции вдоль контура, охватывающего токи текущие в одном направлении, и ток текущий в противоположном направлении.

Ответ: .

3. По сечению проводника равномерно распределён ток плотностью . Найти циркуляцию вектора напряжённости вдоль окружности радиуса , проходящей внутри проводника и ориентированной так, что её плоскость составляет угол с вектором плотности тока.

Ответ: .

4. Диаметр тороида без сердечника по средней линии равен 30 см. В сечении тороид имеет круг радиусом r = 5 cм. По обмотке тороида, содержащей витков, течёт ток (рис. 3.7). Пользуясь законом полного тока, определить максимальное и минимальное значение магнитной индукции в тороиде.

Ответ:

4. МАГНИТНОЕ ПОЛЕ ТОКОВ, ТЕКУЩИХ

ПО ПРОСТРАНСТВЕННЫМ ПРОВОДНИКАМ

Примеры решения задач

1. Тонкий провод с изоляцией образует спираль из большого числа плотно расположенных витков, по которым течёт постоянный ток .

Радиусы внутреннего и внешнего витков равны и (рис. 4.1). Найти магнитную индукцию в центре спирали.

Решение.

Магнитная индукция элемента тока , проходящего по спирали в интервале равна

где

Линейную плотность тока в плоской спирали найдём по формуле

.

,

.

2. Ток течёт вдоль длинной тонкостенной трубы радиусом . Вдоль всей длины трубы прорезана узкая щель шириной . Определить магнитную индукцию внутри трубы, если .

Решение.

Если бы труба была сплошная, то внутри нее магнитная индукция должна равняться “нулю”, согласно теореме о циркуляции вектора .

Для решения этой задачи применим искусственный метод. Будем считать, что ток течёт вдоль всей трубы в одну сторону, а по щели ток - в противоположную. Тогда по принципу суперпозиции суммарный ток в щели равен нулю, и поле внутри трубы (в т. А на расстоянии ) формируется током (рис. 4.2).

В этом случае можно применить формулу для определения магнитной индукции прямолинейного проводника

,

где , - линейная плотность тока .

Окончательно

.

3. Тонкая лента шириной свёрнута в трубку радиусом R. По ленте течёт равномерно распределённый по её ширине ток I. Определить модуль вектора в произвольной точке на оси трубки.

Решение.

Зададим положение интересующей нас точки О на оси трубки углами и (рис. 4.3). Выделим кольцевой элемент шириной на расстоянии от точки О и рассчитаем магнитную индукцию в точке О, создаваемую элементом , используя формулу для кругового тока

,

где - ток, протекающий по элементу .

Так как , то .

Далее необходимо перейти от переменной к переменной .

.

Продифференцируем полученное выражение

,

.

Таким образом,

,

.

Эта формула справедлива и для соленоида, т.к. - ток, текущий по единице длины соленоида

.

4. Определить индукцию магнитного поля тока, равномерно распределённого по бесконечной плоскости с линейной плотностью .

Решение.

В

Рис. 4.4 а

ыберем на плоскости два элемента бесконечной длины и ширины , по которым течёт ток (рис. 4.4а). Элементы расположены симметрично относительно оси , на которой находится интересующая нас точка . Разложим вектор магнитной индукции поля, созданного одним из элементов тока в точке на составляющие и . Составляющие , созданные симметричными элементами тока , направлены в противоположные стороны, поэтому

.

Результирующее поле нужно искать, как сумму составляющих всех элементарных токов. Воспользуемся формулой индукции магнитного поля, создаваемого бесконечно длинным прямолинейным проводником

,

где , а - расстояние от элемента тока до точки .

Нас интересуют составляющие

.

Произведем замену переменной

; , .

.

В результате интегрирования получим

.

Результирующий вектор будет направлен параллельно плоскости вверху – налево, внизу – направо, для указанного на рис. 4.4 а направления тока.

Д

Рис. 4.4 б

анную задачу можно решить и с использованием теоремы о циркуляции вектора . Зная, как расположены в этом случае линии индукции магнитного поля, выберем контур в виде прямоугольника 1234 (рис. 4.4 б). Тогда по теореме о циркуляции , где - длина стороны контура, параллельная плоскости с током. Из последнего равенства находим то же самое выражение

.

Магнитное поле как с одной стороны пластинки, так и с другой – однородное.

5. Определить индукцию магнитного поля тока, равномерно распределенного по двум параллельным бесконечным плоскостям с линейными плотностями и .

Решение.

И

Рис. 4.5

спользуя решение задачи 4 и принцип суперпозиции, можно сделать заключение, что в пространстве между пластинами направлены в одну сторону (рис.4.5) и магнитная индукция результирующего поля равна сумме . Вверху и внизу системы пластин индукции и направлены в противоположные стороны и компенсируются. Результирующее поле равно нулю.

6. Определить индукцию магнитного поля в точке А (рис. 4.6) тока I, равномерно распределенного по бесконечно длинной, очень тонкой металлической ленте шириной b.

Решение.

Воспользуемся формулой расчета магнитной индукции, создаваемой бесконечно длинным прямолинейным проводником

, где .

Перейдем от переменной х к переменной β

.

Таким образом,

,

_.

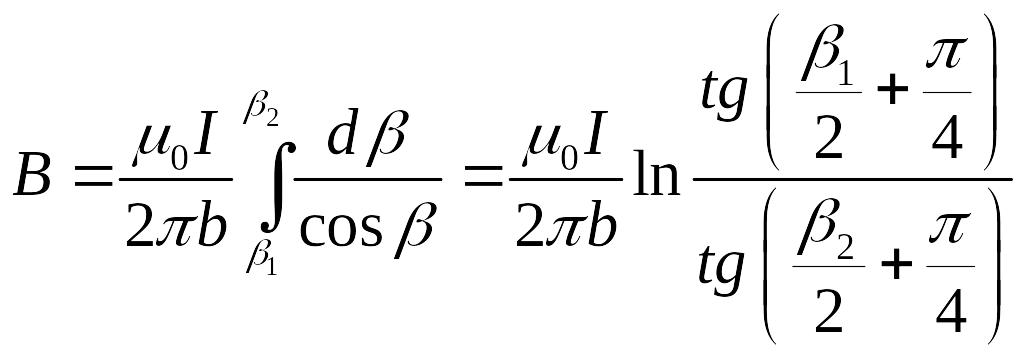Составляющие и найдем из следующих соотношений

,

.

,

.

Если лента становится бесконечно широкой, то

, а и ,

.

7

Рис.4.7

. Однородный ток плотности j течет внутри неограниченной пластины толщины d параллельно ее поверхности. Найти индукцию магнитного поля этого тока во всех точках пространства вне пластины.

Решение.

Воспользуемся формулой расчета магнитной индукции, создаваемой бесконечно длинным прямолинейным проводником

,

где , r – расстояние от выбранного элемента dx до интересующей нас точки А (рис. 4.7).

От элемента dx, расположенного симметрично относительно оси Y справа, составляющая будет положительной, а направлена вправо, следовательно , и результирующий вектор магнитной индукции направлен горизонтально вдоль оси X.

.

Перейдем от переменной х к переменной α

, , .

.

В результате интегрирования получим

.

8. Ток I=11A течет по длинному прямому проводнику, сечение которого имеет форму тонкого полукольца радиуса R=5 см (рис. 4.8). Найти индукцию магнитного поля в точке О.

Решение.

Воспользуемся формулой расчета магнитной индукции прямолинейного проводника бесконечной длины

,

где , j – поверхностная плотность тока.

,

где d – толщина полукольца.

Таким образом,

.

Поверхностную плотность тока j в полукольце найдем из соотношения

.

Учитывая, что составляющие от симметричных относительно оси Y элементов тока и (рис.4.8) направлены в противоположные стороны и компенсируют друг друга, , необходимо искать результирующий вектор магнитной индукции только вдоль оси X.

и ,

, ,

9. Ток I течет по длинному прямому проводнику, имеющему форму полуцилиндра радиуса R. Найти магнитную индукцию на оси О.

Решение.

В

Рис. 4.9

оспользуемся формулой расчета магнитной индукции прямолинейного проводника бесконечной длины, как в задачах 6-8.

,

где dI – ток, текущий через элементарную площадку dS (рис. 4.9), площадь которой в полярных координатах

, ,

где - поверхностная плотность тока.

Как и в предыдущих задачах, нас интересует только горизонтальная составляющая , так как .

Из рис. 4.9 следует, что

,

.

.