
- •Магнитное поле линейных и пространственных проводников с током методические указания
- •Магнитное поле линейных и пространственных проводников с током
- •394026 Воронеж, Московский просп., 14
- •1. Магнитное поле линейных проводников с током Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •2. Магнитное поле соленоида и тороида Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3. Применение теоремы о циркуляции вектора магнитной индукции к расчёту полей Основные законы и формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •5. Магнитное поле вращающихся заряженных тел
- •Основные формулы
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Библиографический список
- •Содержание
Задачи для самостоятельного решения
1.
Катушка длиной
![]() содержит
содержит
![]() витков. По обмотке катушки идёт ток
витков. По обмотке катушки идёт ток
![]() .
Диаметр
.
Диаметр
![]() катушки равен
катушки равен
![]() .
Определить магнитную индукцию в точке,
лежащей на оси катушки на расстоянии
.
Определить магнитную индукцию в точке,
лежащей на оси катушки на расстоянии
![]() от её конца.
от её конца.
Ответ:
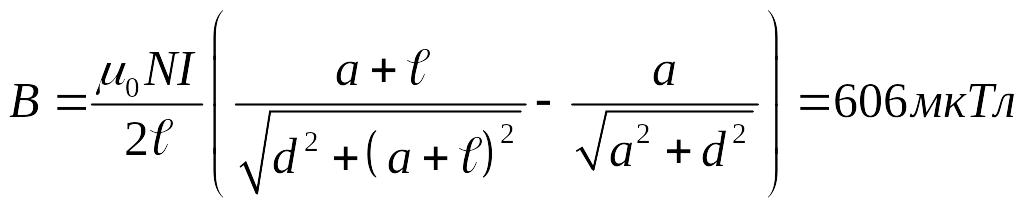 .
.
2.
Обмотка катушки сделана из проволоки
диаметром
![]() .
Витки плотно прилегают друг к другу.
Считая катушку достаточно длинной,
найти индукцию магнитного поля внутри
катушки при силе тока в
.
Витки плотно прилегают друг к другу.
Считая катушку достаточно длинной,
найти индукцию магнитного поля внутри
катушки при силе тока в
![]() .
.
Ответ: В=1,57мТл.
3.
Из проволоки диаметром
![]() надо намотать соленоид, внутри которого
индукция должна быть равна 30,17мТл.
Предельная сила тока, которую можно
пропускать по проволоке равна
надо намотать соленоид, внутри которого
индукция должна быть равна 30,17мТл.
Предельная сила тока, которую можно
пропускать по проволоке равна
![]() .
Из какого числа слоёв будет состоять
обмотка соленоида, если витки наматывать
плотно друг к другу? Диаметр катушки
считать малым по сравнению с её длиной.
.
Из какого числа слоёв будет состоять
обмотка соленоида, если витки наматывать
плотно друг к другу? Диаметр катушки
считать малым по сравнению с её длиной.
Ответ:
из
![]() слоёв.
слоёв.
4.
Требуется получить индукцию магнитного
поля, равную 1267мкТл,
в соленоиде длиною
и диаметром
![]() .
Найти: 1) число ампер-витков, необходимых
для этого соленоида, 2) разность
потенциалов, которую надо приложить к
концам обмотки, если для неё употребляется
медная проволока диаметром
.
Найти: 1) число ампер-витков, необходимых
для этого соленоида, 2) разность
потенциалов, которую надо приложить к
концам обмотки, если для неё употребляется
медная проволока диаметром
![]() .
Считать поле соленоида однородным.
.
Считать поле соленоида однородным.
Ответ: NI=200 ампер-витков.
5. Какую ошибку мы допускаем, при нахождении индукции магнитного поля в центре соленоида, принимая соленоид задачи 3.4 за бесконечно длинный?
Ответ:
![]() .
.
6.
Обмотка соленоида выполнена тонким
проводом, плотно прилегающими друг к
другу витками. Длина
![]() катушки равна
катушки равна
![]() ,
её диаметр
,
её диаметр
![]() .
По обмотке идёт ток. Вычислить размеры
участка на осевой линии, в пределах
которого магнитная индукция может быть
рассчитана по формуле бесконечного
соленоида с погрешностью не превышающей
.
По обмотке идёт ток. Вычислить размеры
участка на осевой линии, в пределах
которого магнитная индукция может быть
рассчитана по формуле бесконечного
соленоида с погрешностью не превышающей
![]() .
.
Ответ:
![]() ;
границы участка отстоят от концов
катушки на
;
границы участка отстоят от концов
катушки на
![]() .
.
3. Применение теоремы о циркуляции вектора магнитной индукции к расчёту полей Основные законы и формулы
Теорема о циркуляции вектора
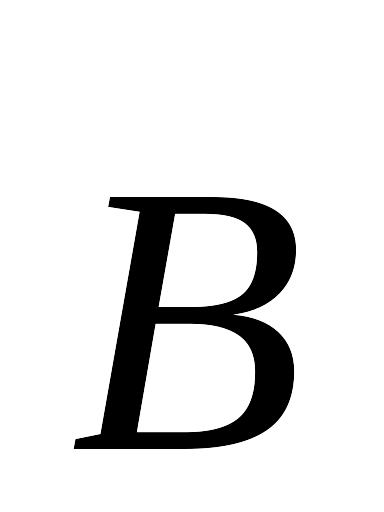 :
:
![]() .
.
Эта
теорема играет примерно ту же роль, что
и теорема Гаусса для векторов
![]() и
и
![]() .
В некоторых случаях – при наличии
специальной симметрии – теорема о
циркуляции оказывается эффективной,
позволяя очень просто находить
.
В некоторых случаях – при наличии
специальной симметрии – теорема о
циркуляции оказывается эффективной,
позволяя очень просто находить
![]() .
.
Закон полного тока:
![]() .
.
Примеры решения задач
1.
Ток
![]() течёт
по бесконечно длинному прямому проводу,
имеющему круглое сечение, радиусом
течёт
по бесконечно длинному прямому проводу,
имеющему круглое сечение, радиусом
![]() .
Найти индукцию поля снаружи и внутри
провода.
.
Найти индукцию поля снаружи и внутри
провода.
Решение.
Линии вектора должны иметь вид окружности, с центром на оси провода. Применим теорему о циркуляции
вектора
для кругового контура радиусом
![]() (рис. 3.1 а):
(рис. 3.1 а):
![]() ,
,
г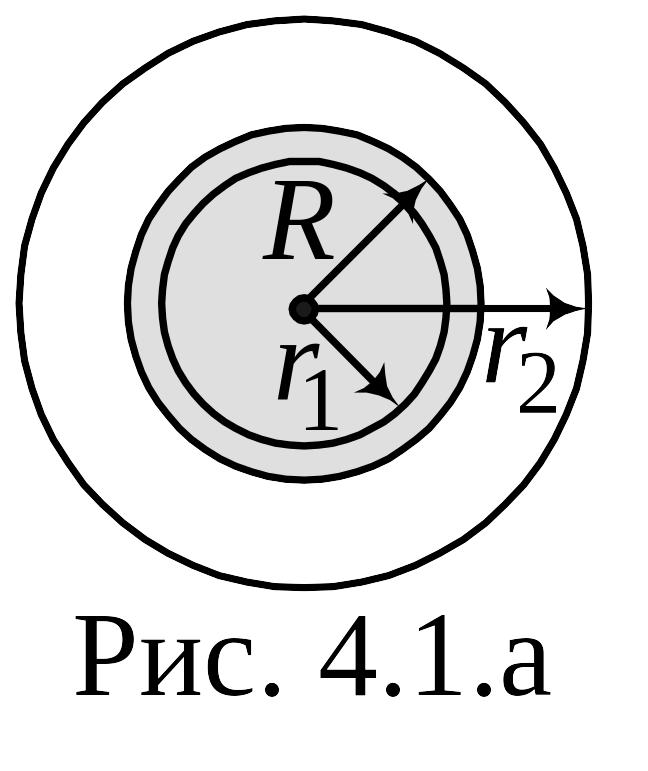 де
де
![]() ,
,
![]() - поверхностная плотность тока.
- поверхностная плотность тока.
Н
Рис. 3.1 а
![]()
 .
.
Поле вне проводника определяется из условия
![]() .
.
З
Рис. 3.1 б![]() показана на рис. 3.1 б.
показана на рис. 3.1 б.
Рис. 4.2 а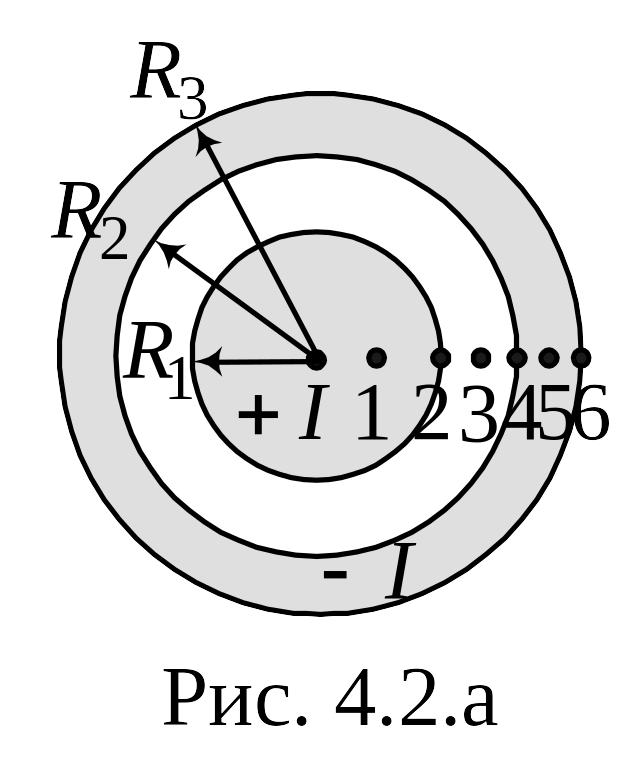
![]() и внешних радиусов
и внешних радиусов
![]() и
и
![]() .
Ток интенсивности
во
внутреннем и внешнем проводниках течёт
в противоположных направлениях. Найти
индукцию магнитного поля во всех точках
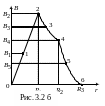
коаксиального кабеля. Построить график
зависимости индукции
.
Ток интенсивности
во
внутреннем и внешнем проводниках течёт
в противоположных направлениях. Найти
индукцию магнитного поля во всех точках
коаксиального кабеля. Построить график
зависимости индукции
![]() от
расстояния от оси.
от
расстояния от оси.
Решение.
Л
Рис. 3.2 а![]() .1)
.1)![]() (рис.3.2 а),
(рис.3.2 а),
![]() ,
,
где
![]() - поверхностная плотность тока,
- поверхностная плотность тока,
![]() - площадь охватываемая контуром.
- площадь охватываемая контуром.
![]() ,
,
![]() .
.
2)
![]() ,
,
![]() ,
,
![]() .
.
3)
![]() ,
,
![]() ,
,
![]() .
.
4)
![]() ,
,
![]() ,
,
![]() .
.
5)
![]() ,
,
 ,
,
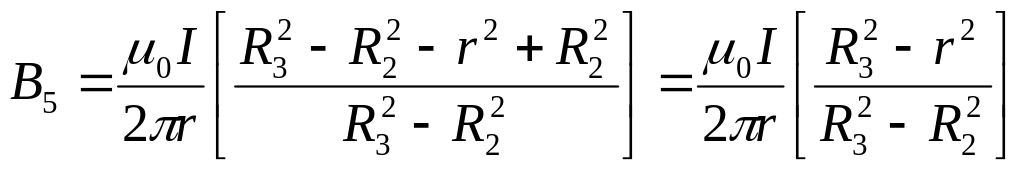 .
.
6)
![]() ,
,
![]() ,
,
![]() .
.
На рис. 3.2 б представлен график зависимости индукции от расстояния от оси проводника. Из данного графика следует, что магнитное поле сосредоточено внутри коаксиального кабеля.
3
Рис. 3.3![]() .
По проводу течёт
.
По проводу течёт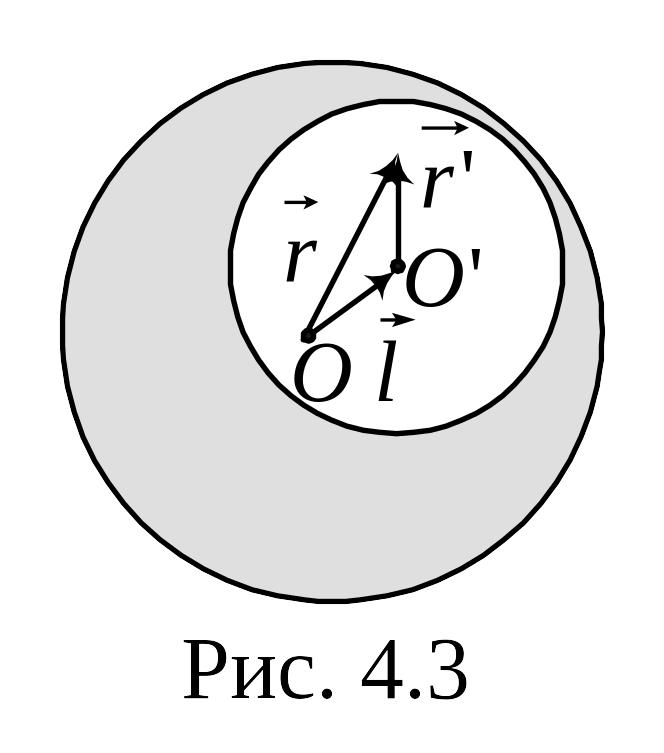 постоянный ток плотности
постоянный ток плотности
![]() .
.
Найти магнитную индукцию внутри полости.
Решение.
Искомую величину можно представить согласно принципу суперпозиции, как
![]() ,
,
где
![]() -
магнитная индукция в том случае, если
бы проводник был сплошным (без полости),
а
-
магнитная индукция в том случае, если
бы проводник был сплошным (без полости),
а
![]() -
магнитная индукция поля в той же точке
от тока, текущего в противоположном
направлении по части провода, которая
удалена, образовав полость кругового
сечения.
-
магнитная индукция поля в той же точке
от тока, текущего в противоположном
направлении по части провода, которая
удалена, образовав полость кругового
сечения.
Найдём
внутри сплошного провода на расстоянии
![]() от его оси (рис. 3.3). Воспользовавшись
теоремой о циркуляции, запишем
от его оси (рис. 3.3). Воспользовавшись
теоремой о циркуляции, запишем
![]() .
.
Найдём также
![]() .
.
Представим
полученные равенства в векторной форме,
учитывая, что
![]() - взаимно перпендикулярны, и искомую
величину
найдём из принципа суперпозиции
- взаимно перпендикулярны, и искомую
величину
найдём из принципа суперпозиции
![]() ,
,
где
![]() .
.
Окончательно
![]() .
.
4.
Ток
![]() течет по длинному прямому проводнику
круглого сечения. Пренебрегая влиянием
вещества проводника, найти магнитный
поток через одну из половин его осевого
сечения в расчёте на один метр длины.
течет по длинному прямому проводнику
круглого сечения. Пренебрегая влиянием
вещества проводника, найти магнитный
поток через одну из половин его осевого
сечения в расчёте на один метр длины.
Решение.
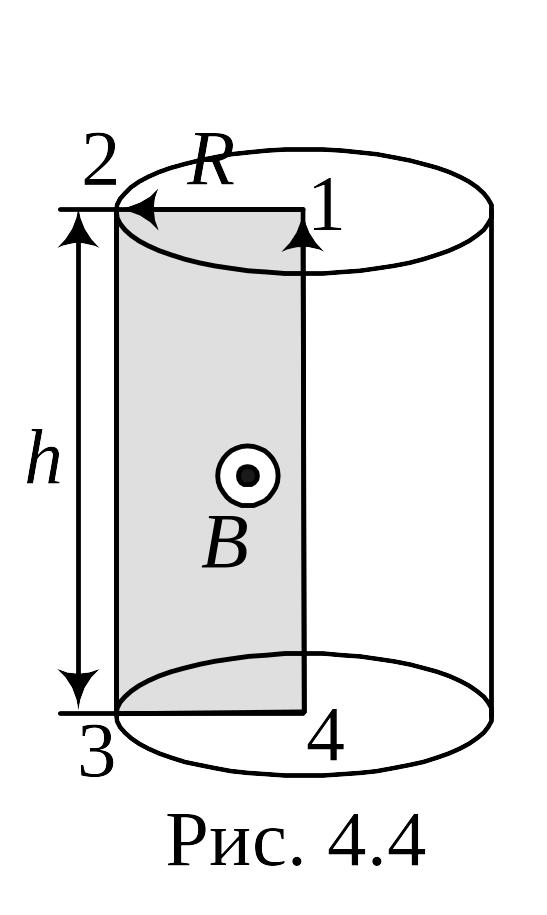
Искомый поток будем искать через сечение 1234 (рис. 3.4). Для этого воспользуемся стандартной формулой для расчёта потока и применим теорему о циркуляции вектора магнитной индукции
![]()
 ,
,
![]() ,
,
где .
Для контура радиуса r можно записать
Рис. 3.4![]()
Поток
через половину осевого сечения высотой
![]() найдётся как
найдётся как
![]() .
.
Поток на один метр длины проводника найдём, поделив найденное значение на
![]() .
.
5.
Определить индукцию магнитного поля
на оси тороида без сердечника, по обмотке
которого, содержащей
![]() витков,
идёт ток
витков,
идёт ток
![]() .
Внешний диаметр
.
Внешний диаметр
![]() тороида
равен
тороида
равен
![]() ,
внутренний
,
внутренний
![]() .
.
Решение.
Для
контура радиуса
![]() ,
проходящего внутри тороида, обмотка
которого содержит
,
проходящего внутри тороида, обмотка
которого содержит
![]() витков,
в соответствии с теоремой о циркуляции,
можно написать
витков,
в соответствии с теоремой о циркуляции,
можно написать
![]()
Учитывая, что - средняя линия тороида
![]() ,
,
найдём
![]()
![]() .
.
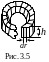 6.
На рис.3.5 показан кольцевой соленоид
прямоугольного сечения. Найти магнитный
поток через это сечение, если ток в
обмотке
6.
На рис.3.5 показан кольцевой соленоид
прямоугольного сечения. Найти магнитный
поток через это сечение, если ток в
обмотке
![]() ,
полное число витков
,
полное число витков
![]() ,
отношение внешнего диаметра к внутреннему
,
отношение внешнего диаметра к внутреннему
![]() и толщина
и толщина
![]() .
.
Решение.
Для контура радиусом , проходящего внутри соленоида, содержащего витков, можно написать
![]() .
.
Магнитный
поток через элемент поверхности высотой
и шириной
![]() равен
равен
![]() .
.
Полный
магнитный поток через сечение соленоида
найдётся интегрированием по
в пределах от
до
![]()
![]() .
.
