
- •В оронеж Строительная механика и конструкции
- •Редакционная коллегия журнала:
- •394006 Г. Воронеж, ул. 20-летия Октября, 84
- •Содержание
- •Анализ процесса влияния наводороживания на напряжённо-деформированное состояние сферической оболочки из титанового сплава
- •Аналитический расчет прогиба стержневой рамы с произвольным числом панелей
- •Формула для расчета прогиба составной внешне статически неопределимой рамы
- •Вероятностная оценка несущей способности поврежденной двутавровой железобетонной мостовой балки
- •Введение
- •1. Краткое описание объекта исследования и произошедшего транспортного происшествия
- •2. Характеристика повреждений несущей крайне балки пролетного строения
- •3. Прочностные расчеты поврежденных балок пролетного строения в детерминированной постановке
- •4. Основные положения методики и результаты количественной оценки параметров, оценивающих надежность характерных сечений поврежденной балки
- •Инженерный метод нелинейного расчёта плитно-балочных систем, применяемых в мостостроениии
- •Введение
- •Анализ методов расчета висячих мостов на статическую нагрузку
- •1. Метод сил
- •2. Полуаналитический метод [2]
- •3. Метод конечных элементов
- •Пк Лира
- •4. Численные исследования
- •Расчёт плоского стального каркаса на постоянную и временную нагрузку c учётом пластических деформаций материала
- •Усиление оснований фундаментов мелкого заложения цилиндрическими оболочками
- •Введение
- •Выводы и практические рекомендации
- •Правила оформления статей
2. Полуаналитический метод [2]
С середины прошлого века в связи с развитием вычислительной техники стали интенсивно развиваться методы расчета висячих мостов с учетом геометрической нелинейности. Рассмотрим не требующий сложных численных расчетов полуаналитический метод, подробно изложенный в монографии [2].
Изложение основных положений метода проведем на примере расчета однопролетного висячего моста, схема которого представлена на рис. 1, а. Воспользуемся теми же допущениями, что и ранее при описании метода сил. Кроме того, ради простоты выводов будем считать подвески нерастяжимыми.
На рис. 4 показана расчетная схема, которая получена из заданной системы моста (см. рис. 1, а) путем разрезания всех подвесок.
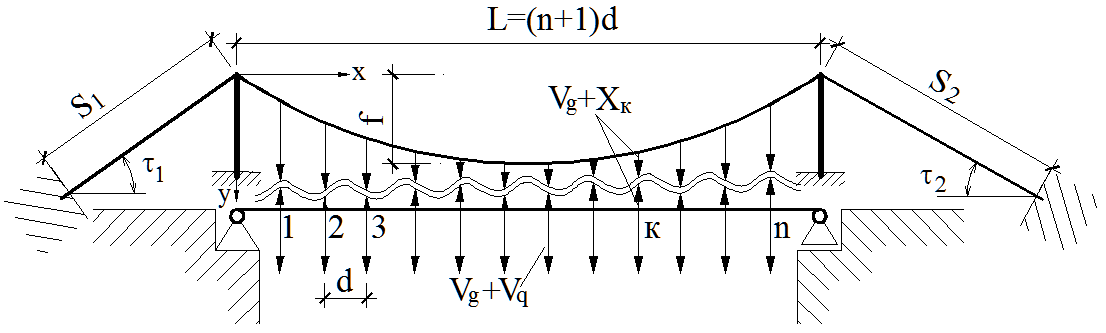
Рис. 4. Расчетная схема моста
При этом кабель и балку можно рассматривать как отдельные системы, имеющие, однако, совместные деформации.
При
монтаже моста сначала к нему прикладывают
постоянную равномерно распределенную
по длине пролета нагрузку g
и тем или иным способом [1, 2]
добиваются, чтобы деформации балки
жесткости от постоянной нагрузки
отсутствовали. Усилия в подвесках от
постоянной нагрузки равны
 .
.
В
процессе загружения моста временной
нагрузкой
 в подвесках появляются дополнительные
усилия
в подвесках появляются дополнительные
усилия
 .
Суммарные усилия, действующие на балку,
будут равны
.
Суммарные усилия, действующие на балку,
будут равны
 . (7)
. (7)
Прогибы балки жесткости в точках прикрепления подвесок обозначим через
 . (8)
. (8)
Вектор
 можно найти
по формуле
можно найти
по формуле
 (9)
(9)
где
 –
матрица влияния прогибов с элементами
–
матрица влияния прогибов с элементами
 , (10)
, (10)
 – изгибающий
момент
в балке в
сечении с координатой x
от единичной силы, приложенной в сечении
с координатой t.
– изгибающий
момент
в балке в
сечении с координатой x
от единичной силы, приложенной в сечении
с координатой t.
Примем
в качестве неизвестных n
величин прогибов
 и распор H.
Для их определения рассмотрим равновесие
k-го
узла кабеля в точке крепления k-й
подвески, предполагая, что на участках
между соседними узлами ось кабеля
представляет собой отрезок прямой (рис.
5).
и распор H.
Для их определения рассмотрим равновесие
k-го
узла кабеля в точке крепления k-й
подвески, предполагая, что на участках
между соседними узлами ось кабеля
представляет собой отрезок прямой (рис.
5).
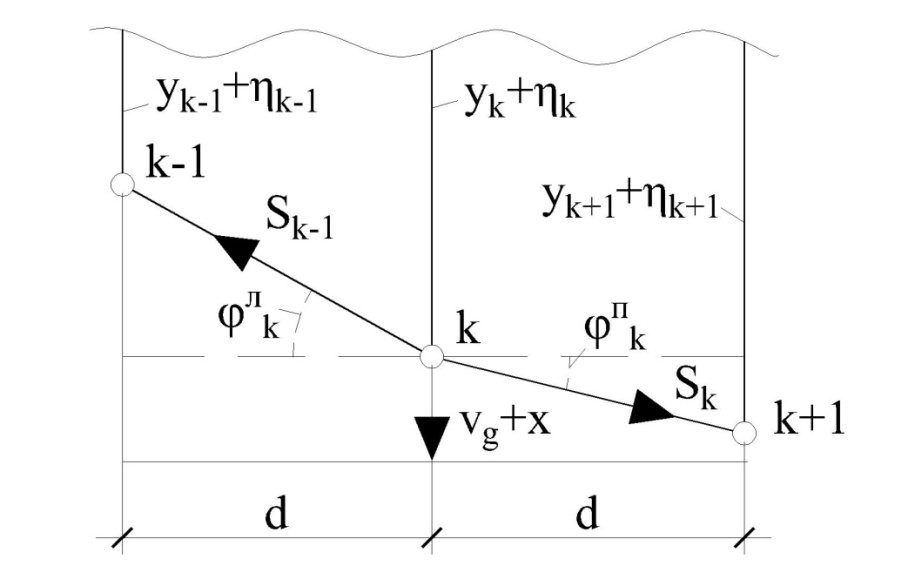
Рис. 5. Равновесий к k-го узла кабеля
На
рис. 5
 – прогиб
кабеля от постоянной нагрузки,
– прогиб
кабеля от постоянной нагрузки,
 – усилие
в кабеле,
– усилие
в кабеле,
 .
Составляя уравнения равновесия в
проекциях на ось y,
после ряда преобразований [2] получим n
уравнений относительно n
прогибов
и распора H:
.
Составляя уравнения равновесия в
проекциях на ось y,
после ряда преобразований [2] получим n
уравнений относительно n
прогибов
и распора H:
 (11)
(11)
где
 (12)
(12)
 , (13)
, (13)
 (14)
(14)

 – единичная
матрица.
– единичная
матрица.
Дополнительное уравнение деформации кабеля получим, воспользовавшись принципом Лагранжа (работа внешних и внутренних сил от постоянной нагрузки на перемещениях от временной нагрузки равна нулю). Этому уравнению можно придать вид [2]
 , (15)
, (15)
где
 (16)
(16)
 ,
(17)
,
(17)
Подставляя
в (15) сумму
 ,
выраженную через
,
выраженную через
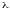 из уравнения (11), получим нелинейное
уравнение относительно параметра
,
решив которое найдем распор из (12) и
перемещения узлов балки по (11).
из уравнения (11), получим нелинейное
уравнение относительно параметра
,
решив которое найдем распор из (12) и
перемещения узлов балки по (11).
Усилия в подвесках находятся по формуле
 . (18)
. (18)
Вектор нагрузок, действующих на балку, имеет вид
 .
(19)
.
(19)
Вектор изгибающих моментов, действующих в сечениях, проходящих через точки крепления подвесок, определяется соотношением
 , (20)
, (20)
где
 –
матрица влияния изгибающих моментов с
элементами
–
матрица влияния изгибающих моментов с
элементами
 .
.
Возможно обобщение изложенной методики для расчета трехпролетных висячих мостов, выполнение расчетов с учетом податливости и наклона подвесок и влияния температуры и т.д. [2].
