3.3. Разработка алгоритма диагностики утечек с учетом помех от стохастичности потребления в системе газоснабжения

Рассмотрим алгоритм обнаружения естественных утечек в системах газоснабжения, когда помехи создаются не только в приемнике информации за счет погрешности вычислений, но и внешними источниками. В качестве внешних источников помех выступают обычные потребители газа в силу стохастичности их заявок.

Утечка рассматривается как заданная функция координат и времени , определяемая из тех же соображений, что и в пп. 3.2. Ее величина аддитивно смешивается с гауссовым шумом ξ(t), который по-прежнему будем считать некоррелированным, однако его интенсивность, то есть дисперсия σ², оказывается неизвестной. При переходе к непрерывному наблюдению шум будем считать белым со спектральной плотностью N₀.

Поставленная задача означает [74], что наблюдается выборка

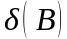(3.50)

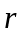где с вероятностью p₁; с вероятностью 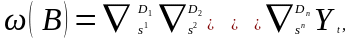; 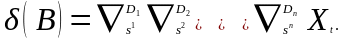. Корреляционная матрица гауссова шума , где δ_ij - символ Кронекера, σ² - величина неизвестная и может считаться распределенной равномерно в некотором диапазоне 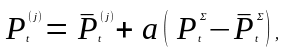. Оптимальный обнаружитель утечки должен составлять [74] отношение правдоподобия

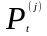(3.51)

где 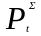и - оценки максимального правдоподобия дисперсии шума, полученные в предположении о наличии и об отсутствии утечки соответственно.

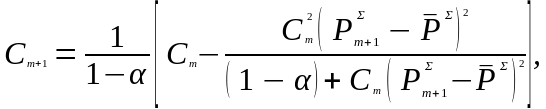Величины плотностей вероятностей и определяются выражениями

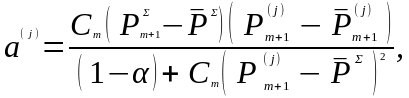
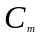(3.52)

так что

(3.53)

Величины и , определяемые из уравнения

(3.54)

имеют вид

(3.55)

Поэтому

(3.56)

Согласно (3.16) отношение правдоподобия (3.56) должно сравниваться с порогом

(3.57)

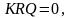где и 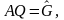определяются из (3.24) как

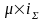
(3.58)

так как

(3.59)

где введены обозначения .

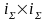
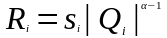Сравнение с порогом (3.57) отношения правдоподобия (3.56) после подстановки (3.58) приводит к следующему алгоритму.

Принимается решение о наличии утечки, если

(3.60)

или

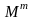(3.61)

При выполнении обратного неравенства принимается решение об отсутствии утечки.

Таким образом, оптимальный адаптивный обнаружитель должен в данном случае составлять оценки неизвестной дисперсии шума в предположениях, соответствующих обеим конкурирующим гипотезам, и сравнивать с порогом отношение этих оценок.

Характеристики оптимального обнаружителя утечки [74] определяются следующим образом. Учитывая, что

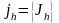(3.62)

отношение оценок дисперсий шумов находятся как

(3.63)

Для нахождения характеристик обнаружения определим вероятность

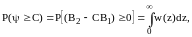(3.64)

где 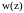- плотность вероятности для величины 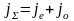, определяемой как

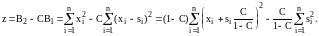(3.65)

Откуда ясно, что 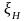нецентральное - распределение. При больших n действует гауссово приближение

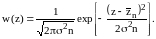(3.66)

При 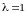будем иметь

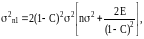(3.67)

а при

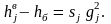(3.68)

где

Учитываем выражение

(3.69)

где 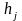- интеграл вероятности.

Соответственно вероятность ложной тревоги:

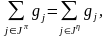, (3.70)

вероятность правильного обнаружения:

, (3.71)

где 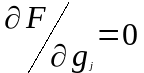- отношение сигнал / шум.

Кривая D(F) при и построена на рис. 3.3, где она сравнивается с характеристикой обнаружения при известной интенсивности шума.

Из выражений (3.70), (3.71) легко получить асимптотическое представление характеристик обнаружения при 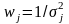[74]. Представляя порог из (3.60) в виде

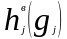(3.72)

где 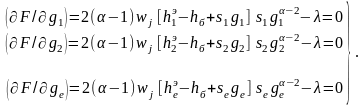- порог при отсутствии априорной неопределенности, и имея в виду, что при 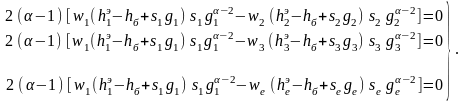, получаем

(3.73)

где и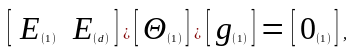 - вероятности ложной тревоги и правильного обнаружения при отсутствии априорной неопределенности.

Рис. 3.3. Характеристики обнаружения сигнала в шуме неизвестной (1)

и известной (2) интенсивности

Для нахождения алгоритма обнаружения, который следует применять при наблюдении непрерывной реализации случайного процесса , воспользуемся рекомендациями [74].

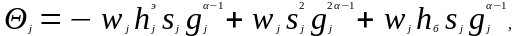
Если осуществить формальный предельный переход в (3.60), (3.61) при то порог

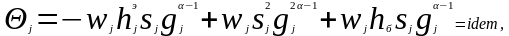(3.74)

а при единичном пороге (3.61) преобразуется к виду

(3.75)

и после перехода к пределу получается следующее условие принятия решения о наличии утечки:

(3.76)

где 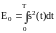- энергия сигнала.

Этот алгоритм и следует применять, если 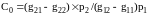представляет собой величину порядка единицы. Однако, учитывая, что, с одной стороны, могут иметь место соотношения коэффициентов потерь и априорных вероятностей, при которых весьма велико либо весьма мало, а с другой стороны, реальный шум не является белым, а имеет полосу _, получается следующий алгоритм принятия решения о наличии утечки:

(3.77)

где порог C определяется (3.60) при 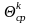- время наблюдения. Характеристики обнаружения получаются из (3.70) и (3.71) при указанном значении и при отношении сигнал / шум 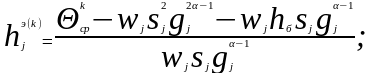где - двусторонняя спектральная плотность шума в полосе Δf_.

_{Следует учесть, что x(t) в (3.77) – это уже не белый, а реально существующий шум, так что вопрос о существовании интегралов не возникает. Конечно, алгоритм (3.77), согласно [138], строго говоря, не оптимален. Оптимальный алгоритм нужно было бы строить с помощью функционала отношения правдоподобия для случая коррелированного гауссова шума. Однако при больших 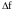алгоритм (3.77) является достаточно хорошим приближением к оптимальному, переходя при единичном пороге в (3.76).}

_{Алгоритм последовательного анализа, определяемый соотношениями (3.67)–(3.69) при подстановке в них выражений (3.56), (3.58), принимает следующий вид. На каждом n-ом шаге наблюдений отношение оценок дисперсии шума 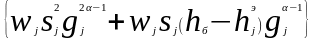сравнивается с двумя порогами} и . _{В случае принимается решение об отсутствии утечки, а в случае 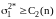– решение о ее наличии. При 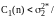наблюдение продолжается. Величины порогов определяются как}

(3.78)

При построении рекуррентного адаптивного алгоритма обнаружения в данном случае удобно подставить (3.60) на n - м шаге в виде

(3.79)

Для левой части неравенства (3.79) непосредственной подстановкой (3.55) находится рекуррентное соотношение

(3.80)

которое должно дополняться рекуррентным соотношением для оценок и . Для последних, исходя из (3.55), находятся точные формулы

(3.81)