3.4. Разработка алгоритма диагностики утечек с неизвестной амплитудой при учете помех от стохастичности потребления в системе газоснабжения

Выше рассмотрены случаи обнаружения утечки с неизвестной амплитудой в шуме, обладающем заданной интенсивностью, либо утечки заданной величины в шуме с неизвестной интенсивностью. Поставим теперь комбинированную задачу, являющуюся важным случаем диагностики утечек, в котором как амплитуда, так и интенсивность шума неизвестны одновременно.

Пусть в моменты наблюдается выборка 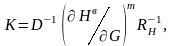случайного процесса , которая может состоять из компонент шума ξ(t) либо из компонент суммы сигнала заданного вида с неизвестной амплитудой α и шума. Интенсивность шума от стохастичности потребления при этом считается неизвестной.

Тогда определяемую приемником информацию об утечке 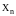можно записать в виде [74]

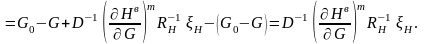(3.82)

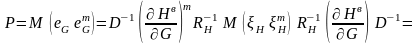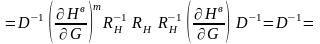
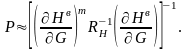
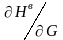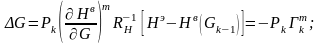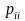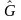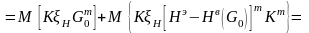
где с вероятностью с вероятностью - заданный вектор , где определяется из тех же соображений, что и в пп. 3.2; - случайный параметр, который по-прежнему будем считать распределенным равномерно в диапазоне Δα=α₂-α₁. Шум является гауссовым с корреляционной матрицей 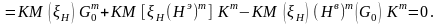- неизвестная интенсивность шума, которая распределена равномерно в интервале .

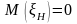Согласно приведенным выше результатам оптимальный алгоритм обнаружения состоит в сравнении с соответствующим порогом отношения правдоподобия:

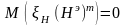(3.83)

где применяются введенные ранее обозначения, а * обозначены оценки максимального правдоподобия соответствующих параметров.

Плотность вероятности и оценка определяются вторыми формулами (3.52) , (3.55) и соответственно

(3.84)

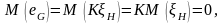(3.85)

Плотность вероятности находится как

(3.86)

Оценки максимального правдоподобия 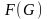и находятся из системы уравнений

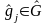
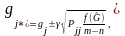(3.87)

После преобразований эти уравнения примут вид

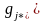
(3.88)

откуда

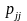(3.89)

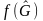(3.90)

Отношение правдоподобия (3.83) определяется как

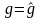(3.91)

Здесь, как и ранее, принято

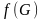
Отношение (3.91) должно сравниваться с порогом

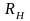(3.92)

Величина 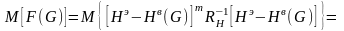относится к ситуации, когда имеется только шум неизвестной интенсивности, и поэтому определяется второй из формул (3.58):

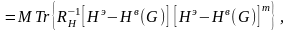(3.93)

где

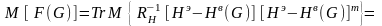
Величина 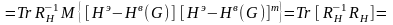в соответствии с (3.5) определяется как

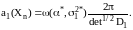(3.94)

Учитывая независимость и равномерность распределения для и , можно показать [75], что Матрица D₁ находится как

(3.95)

Согласно (3.88)

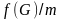(3.96)

где

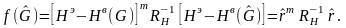
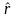
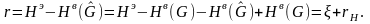
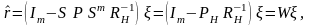(3.97)

Отсюда

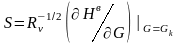(3.98)

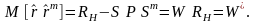(3.99)

В результате порог 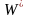имеет вид

(3.100)

Сравнение с порогом (3.100) отношения правдоподобия (3.91) эквивалентно алгоритму, в соответствии с которым принимается решение о наличии утечки, если

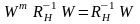_(3.101)

где порог 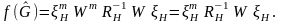определяется так:

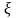(3.102)

а - оценочное значение нормированного отношения сигнал/ шум Если же считать, ч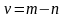то , то

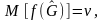(3.103)

где 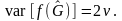- оценочное значение диапазона изменения отношения сигнал/шум (при заданном диапазоне изменения амплитуды сигнала и оценочном значении интенсивности шума, полученном в предположении о наличии утечки). Выражение в скобках в (3.103) совпадает с соответствующим порогом, определяемым соотношением (3.31), при обнаружении утечки с неизвестной амплитудой в шуме известной интенсивности. Разница заключается в том, что истинный диапазон Δh заменен оценочным Δh*. Структура алгоритма, включая и зависимость порога от 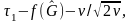, оказалась такой же, согласно [74], как и при обнаружении известной утечки в шуме неизвестной интенсивности.

При непрерывном наблюдении алгоритм (3.101) в результате предельного перехода принимает следующий вид:

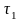(3.104)

где

(3.105)

Порог определяется так:

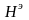(3.106)

где

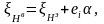(3.107)

а 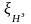- максимальная энергия сигнала.

В отношении алгоритма (3.104) в работе [74] указаны те же условия, которые были применены к алгоритму непрерывных наблюдений в пп. 3.3. Шум здесь подразумевается не белым, а имеющим полосу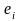 _{. А алгоритм (3.104) является лишь приближением к оптимальному алгоритму. При применении процедуры оптимизации алгоритмы (3.101) и (3.104) остаются в силе, однако порог} становится постоянным и определяется как

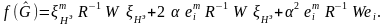(3.108)

Характеристики обнаружения могут быть получены в соответствии с [74]. Если пренебречь зависимостью порога X_n, то алгоритм будет следующим. Решение о наличии утечки принимается в случае, если

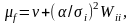(3.109)

где

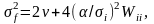(3.110)

После введения линейного преобразования

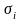(3.111)

с такой матрицей , что 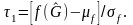, получим

_(3.112)

то есть

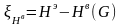_(3.113)

В силу рассмотренных ранее свойств и G функция корреляции

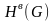
(3.114)

При нахождении математического ожидания 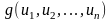учтено, что согласно (3.110) и (3.111)

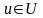(3.115)

Из условия 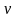т. е. 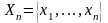следует:

(3.116)

Отсюда при а значит, при

(3.117)

при математическое ожидание , следовательно, и Из (3.110)

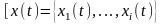(3.118)

Таким образом,

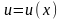(3.119)

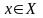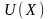где - статистически независимые нормально распределенные величины с параметрами ( ) при и при .

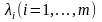Алгоритм обнаружения сводится к сравнению с порогом 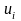величины

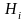(3.120)

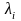
Для расчета характеристик обнаружения необходимо найти вероятность . Очевидно, что

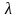(3.121)

где - интегральный закон распределения для .

Если ввести

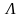(3.122)

то

(3.123)

где 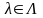- интегральный закон распределения величины 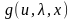, т. е. распределение Стьюдента [44]. При 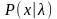это центральное, а при 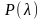нецентральное распределение Стьюдента.

В результате характеристики обнаружения могут быть найдены по таблицам и графикам математической статистики, причем ими следует пользоваться при малых вероятностях ложной тревоги F. При больших F и достаточно больших n хорошим приближением является

(3.124)

В результате алгоритм обнаружения сводится к тому, что решение о наличии утечки принимается, если

(3.125)

что с точностью до множителя совпадает с алгоритмом обнаружения сигнала с неизвестной амплитудой в шуме известной интенсивности. При этом характеристики обнаружения определяются соотношениями (3.36) и (3.37). Характеристики обнаружения при n=10 и h=8 приведены на рис. 3.4.

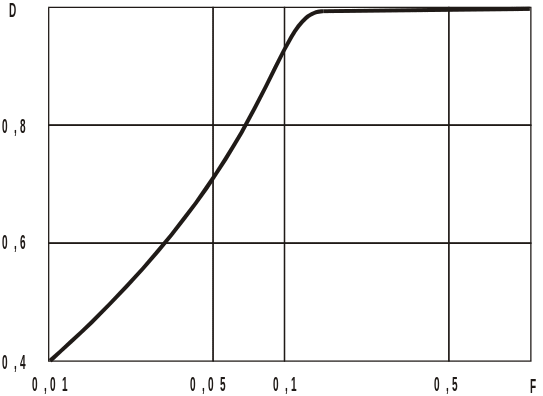
Рис. 3.4. Характеристика обнаружения сигнала с неизвестной амплитудой

в шуме неизвестной интенсивности

Адаптивный алгоритм последовательного анализа при обнаружении утечки с неизвестной амплитудой в шуме неизвестной интенсивности при тех же предположениях, что и в ранее рассмотренных задачах, сводится к сравнению на каждом - м шаге наблюдений отношения

(3.126)

с двумя порогами:

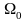(3.127)

где 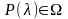- оценочное значение диапазона изменения отношения сигнал/шум, полученное на -м шаге наблюдений. Структура порогов получилась такой же, как (3.75). Как показано в [74], эти пороги являются случайными за счет зависимости .

Для нахождения рекуррентного адаптивного алгоритма обнаружения подобно (3.76) можно представить правило принятия решения о наличии утечки на 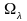- м шаге наблюдений в виде

(3.128)

Подставляя (3.126) в левую часть (3.128) и полагая, что при достаточно больших n можно использовать неравенство 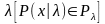, получим

(3.129)

Эту формулу, согласно [74], нужно дополнить рекуррентными соотношениями для 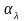, и , которые получаются на основе (3.90) и (3.84). В том же приближении, что и (3.129), они имеют вид

(3.130)