ГОУВПО «Воронежский государственный технический университет»

А. В. Володько И. М. Кириллов В. И. Юдин

РАСЧЕТ ОТКРЫТЫХ ОПТИЧЕСКИХ РЕЗОНАТОРОВ ГАЗОВЫХ ЛАЗЕРОВ МЕТОДОМ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ

Утверждено редакционно-издательским советом

университета в качестве учебного пособия

Воронеж 2011

УДК 535.8

Володько А. В. Расчёт открытых оптических резонаторов газовых лазеров методом интегральных уравнений: учеб. пособие / А. В. Володько, И. М. Кириллов, В. И. Юдин. Воронеж: ГОУ ВПО «Воронежский государственный технический университет», 2011. 84 с.

Учебное пособие посвящено рассмотрению ряда вопросов, связанных с расчётом свойств оптических резонаторов методом интегральных уравнений, в частности, рассмотрены методы расчёта пустых резонаторов с большим числом Френеля и методы учёта пространственной неоднородности активной среды лазера. Эти вопросы имеют в настоящее время большое прикладное значение, знакомство с ними принесет большую пользу будущим инженерам, расширит их кругозор.

Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 210300 «Радиотехника», специальности 210302 «Радиотехника», дисциплине «Электродинамика и распространение радиоволн».

Учебное пособие подготовлено в электронном виде в текстовом редакторе MS WORD 2003, содержится в файле пособие.doc.

Ил. 47. Библиогр: 7 назв.

Рецензенты: кафедра телекоммуникационных систем Воронежского института МВД России (начальник кафедры д-р техн наук, проф.

О. И. Бокова);

канд. физ.-мат. наук К. А. Зимовец

© Володько А. В., Кириллов И. М., Юдин В. И., 2011

© Оформление. ГОУВПО «Воронежский

государственный технический

университет», 2011

Введение

Последние десятилетия ознаменовались важными научными и практическими результатами, достигнутыми в физической и прикладной оптике. Оптические принципы, методы и аппаратура всё шире проникают в самые различные области науки и техники и играют значительную и постоянно возрастающую роль в ускорении научно - технического прогресса.

Бурное развитие оптики, происходящее на наших глазах, связано с созданием лазеров – принципиально новых (когерентных) источников электромагнитного излучения оптического диапазона. Применение лазерного излучения стремительно расширяется и охватывает практически всю экспериментальную физику, как и многие области техники и технологий. Достаточно упомянуть такие, как волоконно-оптическая связь, средства записи, хранения, обработки и защиты информации, физическая обработка любых материалов, медицинская аппаратура и экологические системы, высокоточное оружие. Лазеры не только привели к возникновению новых современных научных направлений, таких как нелинейная оптика, голография, управление термоядерной реакцией, разделение радиоизотопов, но и оказали большое влияние на классические разделы оптики.

Оптический резонатор является важнейшей частью квантовых генераторов оптического диапазона – лазеров. Именно резонатором в значительной мере определяются такие характеристики как коэффициент заполнения активной среды оптическим полем, частотные и пространственные характеристики излучения и другие. Оптимизация технических характеристик проектируемого лазера возможна только при всестороннем анализе положительных и отрицательных черт данного резонатора. Важную роль в таком анализе играет расчёт пространственного амплитудно-фазового распределения (АФР) поля на зеркалах, а также вычисление величины потерь в резонаторе.

Появление новых типов лазерных резонаторов, в частности, характеризующихся большими числами Френеля, привело к необходимости модернизации существующих методов их расчёта. В большей степени это относится к методу интегральных уравнений, так как именно этот метод позволяет рассчитывать АФР поля в резонаторах, образованных зеркалами практически любой формы.

В настоящем пособии рассмотрены методы расчёта пустых одиночных и связанных оптических резонаторов, а также методы учёта активной среды, заполняющей резонатор.

1. Расчёт одиночных пустых оптических резонаторов

В литературе наибольшее распространение получили несколько взаимосвязанных подходов к расчёту амплитудно-фазового распределения (АФР) поля в резонаторе. В их числе: оптика гауссовых пучков, матричная оптика, метод дифференциальных уравнений, метод интегральных уравнений и другие. Рассмотрим вкратце основные черты названных методов.

Уравнение гауссова пучка, распространяющегося вдоль оси z, можно записать двумя эквивалентными математическими выражениями: первое –

(1)

и второе –

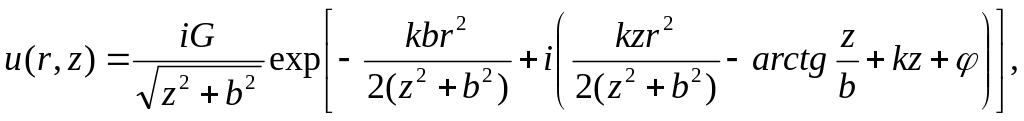(2)

где r – расстояние от точки наблюдения в пучке до оси z; G – амплитудная постоянная; k – волновое число; φ – начальная фаза; b – параметр конфокальности.

Известно, что гауссов пучок с учётом других компонент поля удовлетворяет параболическому приближению волнового уравнения Гельмгольца, а значит, приближённо удовлетворяет уравнениям Максвелла. Из приведённых выражений видно, что второе выражение (2) отличается от первого (1) тем, что в показателе экспоненты разделены действительная и мнимая части, что позволяет отдельно исследовать распределение амплитуд и фаз в пучке и другие его характеристики. Преимущества первого выражения состоят в удобстве согласования гауссового и матричного подходов.

Волновой фронт (поверхность постоянной фазы) гауссова пучка имеет форму параболоида вращения. С хорошей точностью его можно считать сферическим.

Рассмотрим теперь лазерный резонатор, образованный двумя сферическими зеркалами, с радиусами кривизны R1 и R2, расположенными на расстоянии d друг от друга (рис. 1):

Рис. 1

В случае идеальных металлических зеркал функция u (поперечная компонента электрического поля) должна обращаться в нуль на зеркалах. В случае диэлектрических зеркал, постоянные скачки фазы на зеркалах можно исключить из рассмотрения и считать, что поле также обращается в нуль на поверхности зеркал. Используя это условие как граничное, можно показать, что гауссов пучок является модой такого резонатора. Стоячая волна, образуемая гауссовым пучком, имеет вид:

(3)

Для того чтобы амплитуда этой стоячей волны обратилась в нуль, необходимо, чтобы аргумент косинуса стал равным mπ + π/2, а аргумент синуса – m'π, где m' и m – целые числа. Требуя, чтобы волна (3) на оси z в точках её пересечения с зеркалами обратилась в нуль, а также чтобы радиусы кривизны волновых фронтов в точках z₁ и z₂ совпали с радиусами кривизны зеркал, можно получить систему уравнений относительно неизвестных параметров пучка. Разрешая указанную систему, можно выразить параметры пучка через параметры резонатора, и таким образом найти гауссов пучок, являющийся модой данного резонатора.

Метод гауссовых пучков не учитывает потери энергии в резонаторе и поэтому применим только к устойчивым резонаторам в случае, если потерями можно пренебречь.

Рассмотрим выражение (1). Из-за неразделённости действительной и мнимой частей показателя экспоненты характеристики как амплитудного, так и фазового распределений сосредоточены в одном комплексном параметре q:

q = z – ib, (4)

который обычно называют комплексным параметром гауссова пучка, и который характеризует сечение пучка плоскостью z = z₀.

При переходе от одного сечения к другому параметр q изменяется по правилу q₂ = q₁ + l, где l – расстояние, разделяющее сечения 2 и 1. Можно указать более общее правило преобразования q при указанном переходе, а именно:

(5)

где коэффициенты A, B, C, D образуют лучевую матрицу АBCD:

(6)

Рассмотрим прохождение гауссова пучка через квадратичный фазовый корректор, то есть абсолютно тонкую линзу бесконечных размеров. Проходя через квадратичный фазовый корректор, волна приобретает дополнительный набег фазы, равный

(7)

где Р – оптическая сила фазового корректора – величина, обратная его фокусному расстоянию.

Как видно из (7), набег фазы в центре корректора больше (он равен нулю), чем на периферии, где набег фазы – отрицательная величина.

Можно показать, что при прохождении через квадратичный фазовый корректор гауссов пучок остаётся гауссовым пучком, хотя его параметры изменяются. Радиусы кривизны волновых фронтов связаны соотношением:

(8)

где R, R` – радиусы кривизны волновых фронтов в месте расположения фазового корректора; F – фокусное расстояние.

В более общем виде:

или

(9)

Это и есть правило преобразования комплексного параметра гауссова пучка при прохождении его через квадратичный фазовый корректор (линзу). Его можно представить в виде правила ABCD, если фазовому корректору (линзе) сопоставить лучевую матрицу

(10)

которую называют оператором или матрицей прохождения гауссова пучка через линзу.

Действие сферического зеркала так же может быть описано правилом ABCD, если сферическому зеркалу сопоставить матрицу (или оператор отражения)

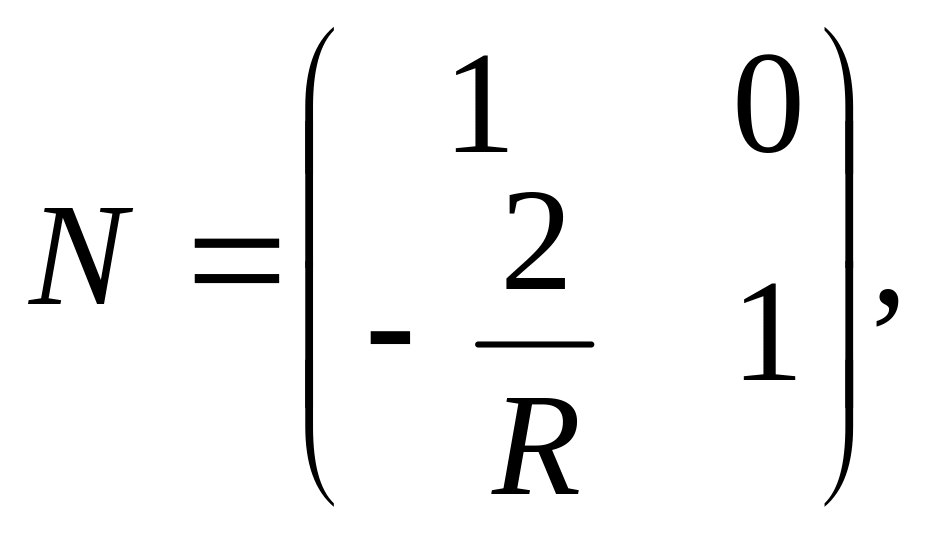(11)

где R – радиус кривизны зеркала.

Величины Р и 1/R могут быть и комплексными, тогда их мнимые части будет характеризовать потери энергии, а корректор будет называться комплексным квадратичным корректором.

Показано [1-3], что лучевая матрица системы, состоящей из гауссовых оптических элементов (элементов, описываемых гауссовой экспонентой), в том числе и матрица лазерного резонатора, равняется произведению лучевых матриц составляющих элементов, расположенных справа налево в том же порядке, в котором их проходит гауссов пучок. У оптической системы, образующей лазерный резонатор, вход и выход совпадают, поэтому комплексный параметр гауссова пучка после его прохода через оптическую систему резонатора должен принять своё исходное значение. Тогда для лазерного резонатора правило ABCD получаем в форме:

, (12)

характерной для замкнутых оптических систем. Соотношение (12) приводит к квадратному уравнению

(13)

разрешая которое относительно q, можно найти комплексный параметр пучка, являющегося продольной модой данного резонатора, а зная связь продольной и поперечных мод, можно найти и поперечные моды.

Матричная оптика является очень мощным и удобным математическим аппаратом для расчёта лазерных резонаторов. Именно простотой применения матричный метод завоевал большую популярность. На данный момент найдены и имеются в литературе [1-4] данные о лучевых матрицах большого числа оптических элементов, таких как участки сред с различными коэффициентами преломления, участки квадратичных сред и другие. Простота нахождения лучевых матриц различных комбинаций элементов позволяет легко рассчитывать различные схемы резонаторов.

Основным недостатком матричной оптики является то, что она применима лишь к резонаторам, состоящим из гауссовых оптических элементов, и часто это ограничивает её применение. Однако большинство оптических элементов с различной степенью точности можно считать гауссовыми. Это делает матричную оптику очень мощным аппаратом для расчёта лазерных резонаторов.

Метод дифференциального уравнения основан на решении уравнения Гельмгольца в параболическом приближении. При использовании данного метода полагают, что оптическая волна распространяется преимущественно в направлении оси z, и общая функция поля представляется как

. (14)

Тогда уравнение Гельмгольца будет иметь вид:

. (15)

В параболическом приближении

, (16)

что приводит к уравнению

(17)

с граничными условиями, соответствующими конкретной задаче.

Главным недостатком этого метода является необходимость применения параболического приближения, что не всегда недопустимо, например, при анализе дисковой конструкции оптического резонатора, характеризующейся большим значением числа Френеля.

Наиболее полное исследование лазерного резонатора, в том числе с учётом дифракционных эффектов, проводится, в основном, методом интегральных уравнений. Именно этот метод позволяет рассчитывать АФР и потери энергии в лазерных резонаторах, образованных зеркалами практически произвольной формы.

Пусть имеется свободное пространство, разделённое на две части непрозрачным плоским экраном с отверстием. Рассмотрим монохроматическую волну, заполняющую обе части пространства. Тогда каждая компонента вектора электрического или магнитного поля будет описываться функцией вида:

ψ(r) = u(r) e^–iωt,

где ω – частота, а функция u(r) – описывает пространственное распределение отдельных компонент электромагнитного поля и является разной для разных компонент. Согласно скалярной теории дифракции имеется связь, задаваемая некоторым интегральным соотношением (дифракционным интегралом), между пространственным распределением поля в плоскости отверстия с пространственным распределением поля за отверстием. В теории оптических резонаторов чаще всего применяется дифракционный интеграл в форме Рэлея-Зоммерфельда, поскольку вывод этого соотношения свободен от внутренних противоречий, характерных для другой формы дифракционного интеграла – формулы Френеля-Гирхгофа.

Введём декартову систему координат, расположенную так, чтобы оси x и y находились в плоскости экрана, а начало координат лежало в плоскости отверстия (рис. 2). Тогда поле в произвольной точке (x₁, y₁) за экраном находится согласно формуле Рэлея-Зоммерфельда [7]:

, (18)

где S – площадь отверстия; ρ – расстояние между элементом отверстия ds и точкой наблюдения; θ – угол между осью z и направлением от элемента ds к точке наблюдения.

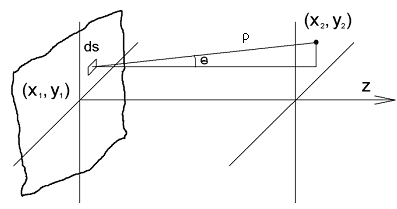
Рис. 2

В том случае, если расстояние ρ много больше максимального размера отверстия S, что соответствует условиям параксиальности, выражение (18) можно существенно упростить. Так как

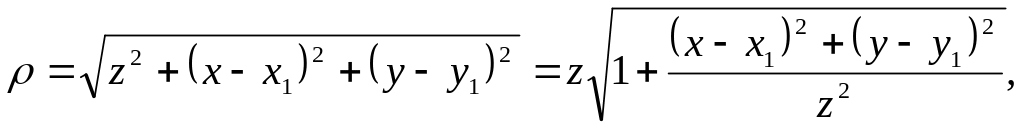(19)

то можно разложить (19) в ряд Тейлора и в знаменателе ограничиться первым членом разложения, то есть ρ ≈ z, cos θ ≈ 1. В показателе экспоненты ограничиться первым членом нельзя, так как возникающая погрешность умножается на большое число k, и неточность расчёта фазы становится сравнимой или большей π. С учётом этого, формула (19) преобразуется к виду:

(20)

Такое упрощение дифракционного интеграла (18) называется приближением Френеля. Оно является достаточно хорошим, если максимальная погрешность в фазе экспоненты, вносимая членами более высокого порядка в разложении корня много меньше π. Показано [3], что это условие выполняется, если:

. (21)

Рассматривая прохождение волны через некоторую оптическую систему и сравнивая получившееся итоговое выражение с лучевой матрицей системы, можно получить интегральное соотношение, описывающее распространение пучка через гауссову оптическую систему с геометрической длиной L и лучевой матрицей ABCD [1, 2]:

(22)

или в цилиндрической системе координат:

(23)

Таким образом, для расчёта прохождения поля через оптическую систему, содержащую негауссовы оптические элементы, необходимо разбить эту систему на подсистемы, в которых негауссовы элементы располагаются на входе или выходе отдельных гауссовых подсистем. Затем для каждой подсистемы строится уравнение (22) или (23), и, зная закон преобразования поля негауссовыми элементами, составляется общее интегральное соотношение.

Рассмотрим теперь применение метода интегральных уравнений к расчёту лазерных резонаторов. В дальнейшем будем рассматривать резонаторы, обладающие цилиндрической симметрией и дальнейшие расчёты проводить в цилиндрической системе координат.

Рассмотрим открытый резонатор общего вида. Пусть обход резонатора лазерным пучком описывается некоторым интегральным оператором Ñ. Пусть имеем интегральное уравнение на собственные значения

χ_iu_i= Ñu_i, (24)

где i = 0, 1, 2, …

Пронумеруем собственные числа этого уравнения в порядке убывания их абсолютной величины:

|χ₀| ≥ |χ₁| ≥ |χ₂| ≥ …

Важной особенность набора функций u_i является свойство полноты, то есть возможность представления пучка с произвольным поперечным АФР ψ в виде:

ψ = Σ a_iu_i, (25)

где а_i – постоянные. Предположим, что в резонатор запущен пучок с поперечным АФР, описываемым функцией ψ. После обхода резонатора, с учётом (24) и (25) имеем

ψ⁽¹⁾ = Σ a_iχ_iu_i (26)

После n-го обхода:

ψ⁽ⁿ⁾ = Σ a_iχ_iⁿu_i. (27)

При n → ∞, поперечное АФР стремится к распределению, описываемому одной из функций u_m, для которой, с одной стороны, a_m ≠ 0, а с другой |χ_m| больше всех прочих коэффициентов в разложении (25) [3].

Найдём явный вид оператора Ñ в случае применения параксиального приближения и использования цилиндрической системы координат. Рассмотрим оптический резонатор, образованный зеркалами произвольной формы. Отражения поля от зеркала произвольной формы можно заменить отражением от плоского зеркала в сочетании с прохождением некоторого оптического элемента, характеризующего форму поверхности зеркала (например, сферическое зеркало можно представить плоским зеркалом в сочетании с собирающей линзой). В отличие от зеркала, поле проходит через этот элемент дважды, что необходимо учитывать при построении функции, описывающей прохождение поля через оптический элемент. Таким образом, приходим к следующей схеме (рис. 3):

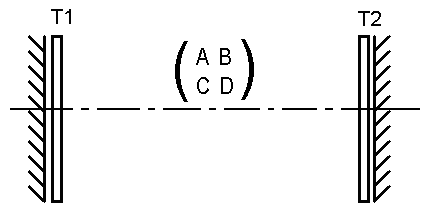
Рис. 3

Введём две системы декартовых координат с общей осью z, таких, что плоскость (r₁,φ₁) расположена вплотную к левому по схеме зеркалу, то есть совпадает с плоскостью оптического элемента Т1, а плоскость (r₂,φ₂) совпадает с плоскостью оптического элемента Т2. Пусть из плоскости (r₁,φ₁) налево начинает распространяться волна, являющаяся модой данного резонатора, заданная поперечным распределением амплитуд и фаз ψ₁. После прохождения элемента Т1, отражения от зеркала и повторного прохождения Т1 получим другое распределение ψ₁` = ψ<sub>1</sub>·T1<sup>2</sup>. Прохождение волны из плоскости (r<sub>1</sub>,φ<sub>1</sub>) к плоскости (r<sub>2</sub>,φ<sub>2</sub>) описывается интегральным оператором L<sub>1</sub>, имеющим вид (23) в случае применения параксиального приближения. Тогда для поперечного распределения поля ψ<sub>2</sub> в плоскости (r<sub>2</sub>,φ<sub>2</sub>) получим ψ<sub>2</sub> = L<sub>1</sub>ψ<sub>1</sub>`, а для поля ψ₂`: ψ<sub>2</sub>` = ψ₂ T2². Прохождение волны из плоскости (r₂,φ₂) к плоскости (r₁,φ₁) описывается интегральным оператором L₂, так же имеющим вид (23). В соответствии с предположением, что исходная волна является модой резонатора, полученное после прохода резонатора поле должно с точностью до константы совпасть с начальным, получаем:

χψ₁= L₂T2²ψ₂,

где ψ₂ = L₁T1²ψ₁.

Записывая явный вид интегральных операторов, приходим к системе интегральных уравнений на собственные значения, описывающих данный резонатор:

(28)

Модули собственных чисел |χ| определяют потери мощности соответствующим им мод, а аргументы – резонансные частоты. Решая задачу на собственные значения (28), можно найти поперечную структуру мод в исходной плоскости. Для получения поперечного распределения в произвольной плоскости внутри и вне резонатора, следует применять соотношение (23).

В некоторых случаях (в частности, в случае гибридного неустойчиво-устойчивого резонатора) систему уравнений (28) можно существенно упростить. Независимость искомого АФР и функций пропускания Т1 и Т2 от угловой координаты позволяют вынести их из-под знака интеграла по угловой координате:

(29)

где а – радиус апертуры зеркал.

Используя интегральное представление функции Бесселя нулевого порядка, из (29) получаем:

(30)

Система (30), в силу одномерности входящих в неё интегралов, требует для своего решения значительно меньше машинного времени, чем система (29). В некоторых случаях возможно и дальнейшее упрощение системы (30).

Случай, когда приближение Френеля неприменимо, то есть случай резонаторов, характеризующихся большим числом Френеля, является значительно более сложным. Это связано с невозможностью аналитического представления интеграла по угловой координате и более высокой скоростью осцилляции подынтегральной функции, что приводит к необходимости применения большого числа узлов интегрирования и значительно снижает скорость численных расчётов.

Рассмотрим гибридный неустойчиво-устойчивый лазерный резонатор (рис. 4):

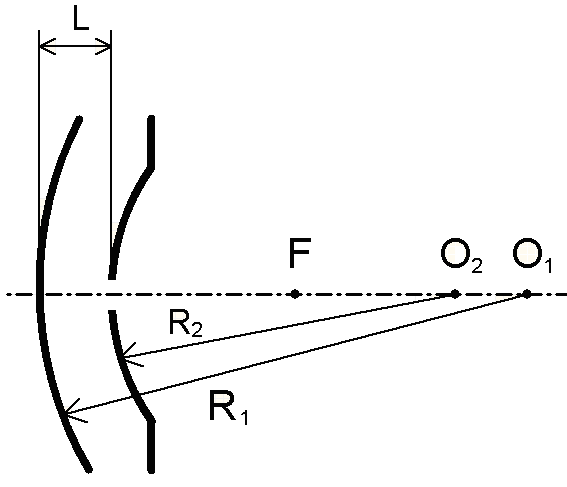
Рис. 4

Построим согласно методу интегральных уравнений систему интегральных соотношений. Пусть от левого зеркала к правому распространяется волна, являющаяся модой данного резонатора. АФР поля этой волны на правом зеркале найдём по формуле Зоммерфельда:

(31)

где ρ – расстояние между расчётными точками на зеркалах.

АФР поля на левом зеркале найдём из соотношения, аналогичного (31):

(32)

Согласно утверждению, что u(r, φ) является АФР поля моды данного резонатора, после обхода резонатора оно с точностью до комплексной константы совпадёт с самим собой. Таким образом, приходим к системе интегральных уравнений на собственные значения:

(33)

Будем рассматривать только те моды, АФР которых не зависит от угловой координаты. Имеем:

(34а)

(34б)

Основная сложность применения метода интегральных уравнений состоит в том, что при большом числе Френеля подынтегральная функция в (34) является быстроосциллирующей, и скорость осцилляций возрастает по мере увеличения числа Френеля. Необходимое число узлов интегрирования при этом также возрастает, что, в свою очередь, приводит к значительному увеличению объёма вычислений. Для его минимизации целесообразно воспользоваться следующим способом.

Заменим сферическое зеркало плоским зеркалом того же диаметра в сочетании с фазовым корректором, обладающим функцией пропускания F₁(r):

(35)

где R₁ – радиус кривизны сферического зеркала.

Зеркало плоско-сферической формы заменим плоским зеркалом такого же диаметра в сочетании с корректором, обладающим функцией пропускания F₂(r). В случае отсутствия окна для вывода излучения, функция F₂(r) имеет вид:

(36)

где R₂ – радиус кривизны сферической части плоско-сферического зеркала; b – радиус апертуры сферической части плоско-сферического зеркала. Видно, что при отсутствии окна для вывода излучения корректор F₂(r) является чисто фазовым и амплитудная часть тождественно равна единице. В случае наличия окна для вывода излучения в выражении для F₂(r) появится амплитудная составляющая и корректор станет амплитудно-фазовым. Очевидно, что наличие резких краёв у окна будет значительно влиять на АФР. Однако у окна для вывода излучения в реальном резонаторе всегда будут иметь место фаски или другие неровности краёв. По этой причине может быть целесообразно «сгладить» края окна. Это можно осуществить, к примеру, при помощи квазигауссовой функции. Тогда выражение для корректора F₂(r) будет иметь вид:

, (37)

где

(38)

в случае отсутствия сглаживания краёв окна;

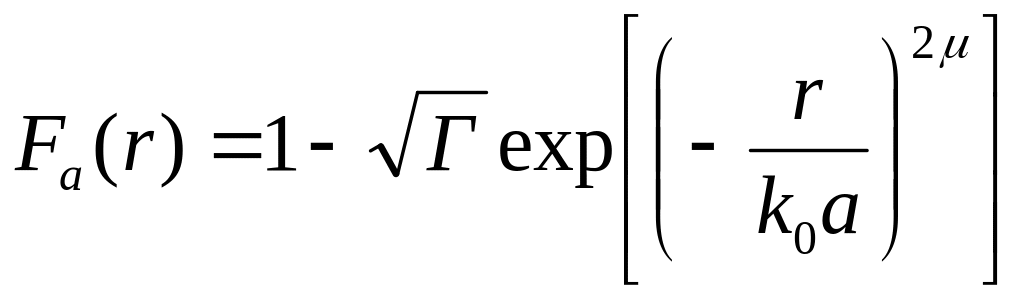, (39)

при использовании сглаживания;

(40)

Г – коэффициент пропускания по мощности материала окна для вывода излучения; R₂ – радиус кривизны сферической части правого зеркала; k₀ – отношение радиуса зеркала к радиусу окна; k₁ – отношение радиуса апертуры сферической части к радиусу апертуры зеркала, μ = 1, 2, ….

Таким образом, получаем эквивалентную схему рассматриваемого резонатора (рис. 5):

Рис. 5

Система интегральных уравнений данного резонатора будет иметь вид:

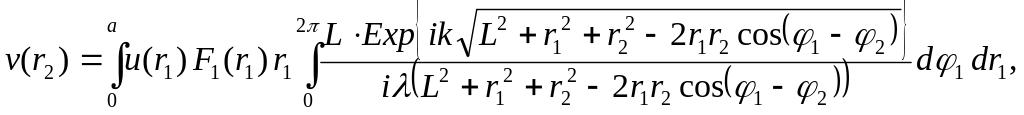(41)

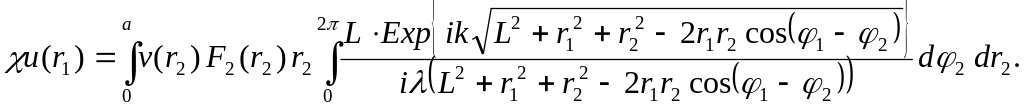
Приведём систему (41) к более удобному для решения виду. Внесём в первом уравнении φ₂, а во втором φ₁ под знак дифференциала. Обозначим φ = φ₁ – φ₂. Заметим, что функция, стоящая под внутренним интегралом, является чётной относительно прямой φ = π. В итоге имеем:

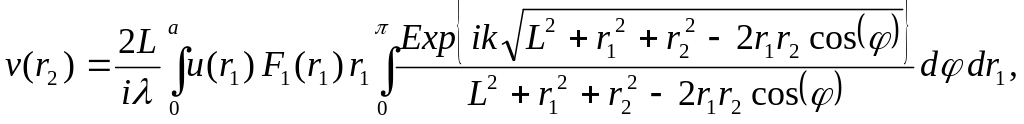
(42)

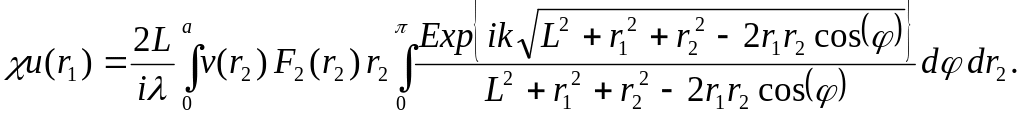
Введём замену переменных . Получим:

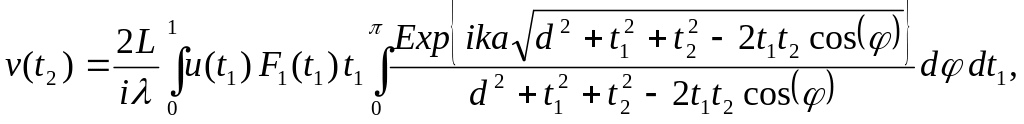(43)

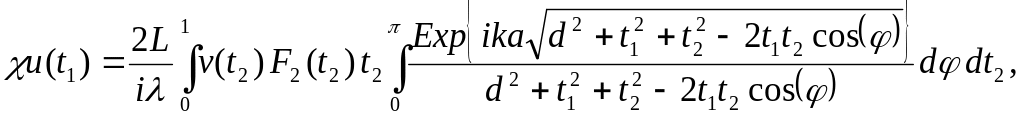
где .

Обозначим

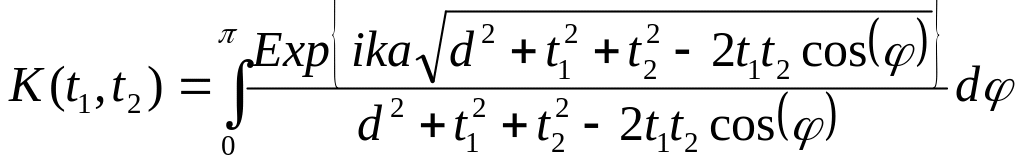. (44)

Таким образом, имеем:

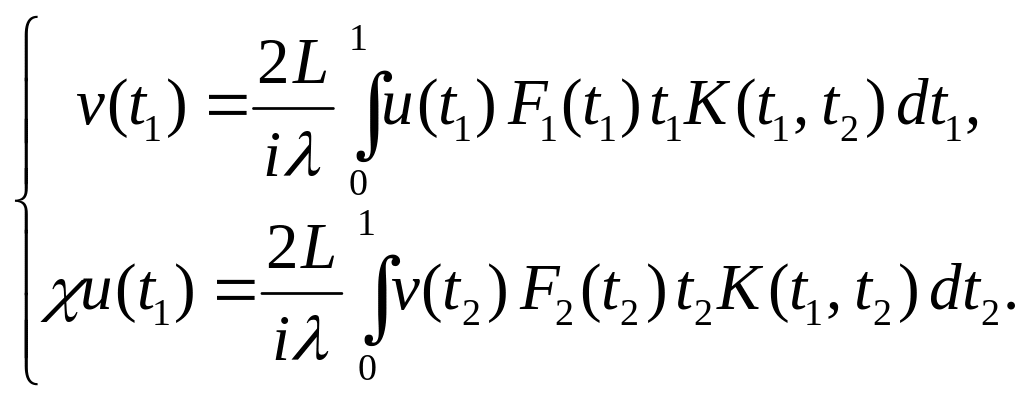(45)

Получили систему из двух зацепляющихся интегральных уравнений, описывающую данный резонатор.

Для решения систем типа (45) наиболее часто применяют метод итераций, допускающий применение разнообразных приближённых (в том числе численных) методов интегрирования. Метод итераций заключается в следующем. Зададим произвольное начальное распределение амплитуд и фаз поля на левом зеркале u₀(t₁). По первому из соотношений (45) найдём распределение поля на правом зеркале v₀(t₂). Затем по второму из соотношений (45) найдём распределение u₁(t₁), по известному u₁(t₁) найдём v₁(t₂) и так далее. Как показано выше, после некоторого числа итераций, соответствующих обходу резонатора электромагнитной волной, АФР будет изменяться слабо. Критерием окончания итерационного процесса служит малость величины σ – разности следующих друг за другом итераций, при этом σ определяется следующим образом [3]:

(46)

где ; * – знак комплексного сопряжения; n – номер итерации.

Приближённое значение величины |χ|² определяется по формуле:

(47)

а потери α в резонаторе – по формуле:

(48)

Так как интеграл (44) не выражается через элементарные функции, при его вычислении необходимо использовать приближённые методы. Рассмотрим, при каких условиях будет выполняться приближение Френеля, позволяющее свести (44) к функции Бесселя нулевого порядка. Для этого необходимо рассмотреть отдельно амплитудную и фазовую части функции, стоящей под интегралом. Для фазовой части имеем:

. (49)

Разложим функцию F(t₁, t₂, φ) в ряд Тейлора, ограничившись двумя первыми членами. Получим:

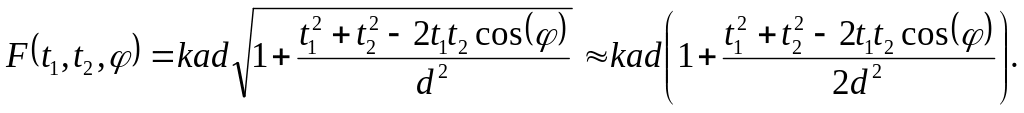(50)

Ряд Тейлора для функции F(t₁, t₂, φ) является знакочередующимся. Известно, что остаток ряда при отбрасывании некоторого числа последних членов по модулю не превосходит модуль первого отброшенного члена для знакочередующихся рядов. Нам необходимо, чтобы погрешность в определении фазы не превышала 0,01π. Таким образом, получаем:

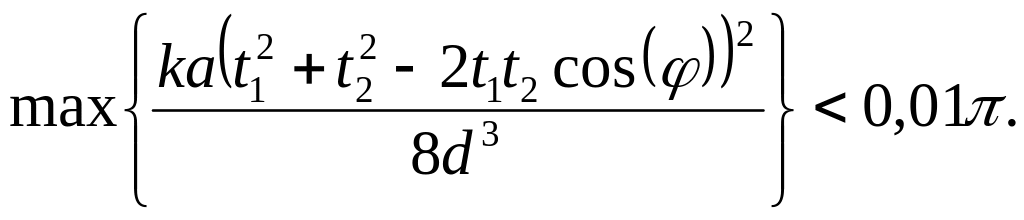(51)

Найдём из (51) диапазон изменения t₁, считая, что t₂ изменяется от 0 до 1, φ – от 0 до π. Максимум в левой части (51) достигается при t₂ = 1, φ = π. Тогда имеем:

(52)

Решая неравенство (52) относительно t₁, получаем:

(53)

Из (53) следует, что применение приближения Френеля возможно только в том случае, если величина превышает единицу. Для амплитудной части имеем:

. (54)

График функции А(t₁, t₂, φ) при трёх значениях параметров t₁ и t₂ приведён на рис. 6:

Рис. 6

Как видно из рисунка, при увеличении параметров t₁ и t₂ разность значений амплитуды на концах интервала интегрирования увеличивается. Однако вместе с этим увеличивается и частота осцилляции в фазовой части, поэтому на промежутке, соответствующей одной осцилляции амплитуда меняется мало. По этой причине, при интегрировании вклад от соседних положительных и отрицательных полуволн примерно компенсируется. Из этих соображений ясно, что более жёсткие условия накладывает фазовая часть подынтегральной функции. Тогда для функции К(t₁, t₂) (симметричной относительно замены своих переменных) при малых t₁ имеем:

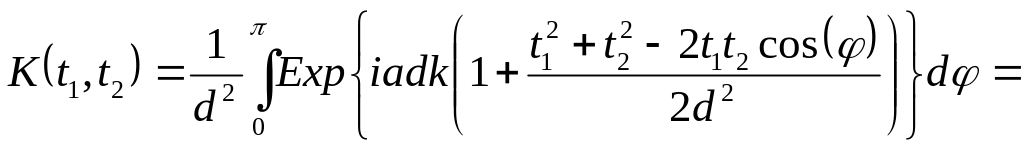
В общем случае:

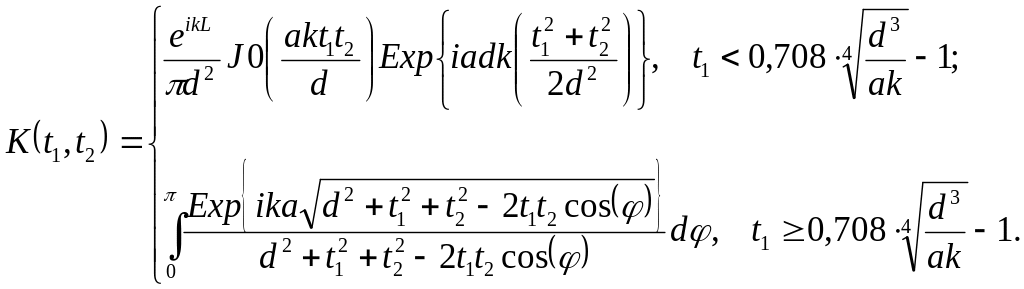(55)

Для численного вычисления интегралов в (45) воспользуемся методом Уэдля. При этом будем искать значения искомой функции в узлах интегрирования, а интеграл (44) будем вычислять при значениях параметров t₁ и t₂ в узлах интегрирования.

При увеличении параметров t₁ и t₂ скорость осцилляции подынтегральной функции в (44) возрастает. На рис. 7 показаны графики зависимости действительной части подынтегральной функции (44) от φ при t₁ = t₂ = 0,005 (пунктирная линия) и t₁ = t₂ = 0,01 (сплошная линия).

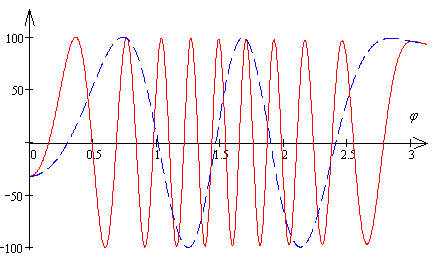
Рис. 7

Для численного вычисления интеграла (44) применим метод Уэдля. С целью увеличения скорости численного интегрирования, число узлов аппроксимации следует сделать переменным, зависящим от количества осцилляций. Определим число осцилляций. Приравняем действительную и мнимую части подынтегральной функции нулю:

(56)

(57)

Выразим из (56) и (57) cos(φ):

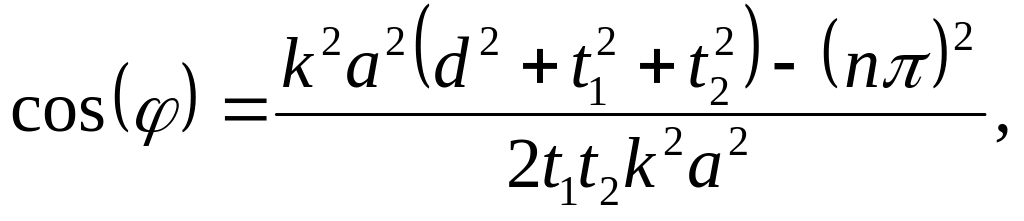(58)

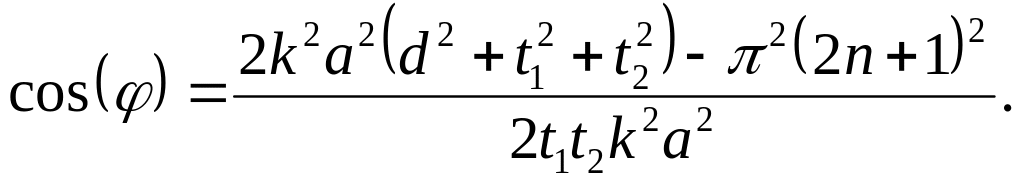(59)

Найдём из (58) и (59) такие значения n, при которых значения правых частей (59) и (59) не превышает по модулю единицу. Обозначим их n_min и n_max. Число корней функции на отрезке [0, π] определится разностью n_max − n_min. Из (58):

(60)

(61)

где floor(a) – целая часть числа а.

Аналогично выражая n_min и n_max из (59), убеждаемся, что число корней действительной и мнимой частей на отрезке [0, π] равны. Для вычисления искомого числа осцилляций N_осц, к числу коней необходимо добавить 2. Таким образом, имеем:

(62)

Число узлов интегрирования Р можно определять следующим образом:

Р = N_осц·q, (63)

где q – число узлов интегрирования, приходящееся в среднем на одну осцилляцию.

Так как согласно методу Уэдля число узлов интегрирования должно быть кратно шести, к числу узлов интегрирования, получаемому по формуле (63), необходимо добавить разницу между шестью и остатком от деления Р на шесть. Скорректированное таким образом количество узлов интегрирования N определится тогда по формуле:

(64)

где mod(a, b) – остаток от деления a на b. Вычисления показывают, что достаточная точность достигается при q ≥ 4. При этом дальнейшее увеличение значения не приводит к значительному повышению точности, но увеличивает время вычислений.

При N_осц > 200 для вычисления (44) становится возможным применение метода стационарной фазы. Учитывая, что на отрезке [0, π] подынтегральная функция в (44) имеет две стационарные точки, получим:

(65)

Так как вычисление интеграла (44) методом Уэдля занимает намного большее время, чем методом стационарной фазы, вычисления по методу Уэдля следует выполнить предварительно и записать результаты в файл на жёстком диске ЭВМ. Это позволит при решении системы (45) методом итераций не вычислять при каждой итерации интеграл (44), что сократит время решения. Предварительное вычисление интеграла (44) только методом Уэдля позволит значительно уменьшить объём массива значений (44) и разместить его целиком в ОЗУ ЭВМ без применения подкачки с жёсткого диска.

Так как рассмотренная методика расчёта ориентирована на вычислительный эксперимент, при решении таких задач, как оптимизация свойств резонатора по тому или иному параметру, может потребоваться многократно вычислять АФР и потери поля при вариации параметров зеркал. Так как в (44) входят только те параметры резонатора, которые определяют число Френеля, при изменении конфигурации зеркал (например, радиуса кривизны или радиуса окна для вывода излучения), нет необходимости производить расчёт ядра (44) заново. Именно представление зеркал в виде амплитудно-фазовых корректоров позволяет получить в этом случае выигрыш по времени вычислений.

Как было отмечено, вычисление интегралов в (45) целесообразно также проводить методом Уэдля. При этом число узлов интегрирования N_R целесообразно положить в шесть раз большим, чем максимальное число осцилляций подынтегральной функции в (44), то есть находить по формуле

(66)

Таким образом, алгоритм расчёта АФР поля и потерь включает в себя два основных этапа: вычисление значений (44) при значении параметров t₁ и t₂, соответствующих узлам интегрирования в (45), таких, чтобы выполнялось условие N_осц < 200 и запись рассчитанных значений на жёсткий диск ЭВМ; решение уравнений (45) методом итераций и вычисление потерь.

Рассмотрим результаты расчётов АФР и потерь поля в неустойчиво-устойчивом резонаторе с использованием изложенного выше метода. Из качественного рассмотрения хода лучей в квазиустойчивом резонаторе ясно, что наиболее оптимальной конфигурацией зеркал является равноугольная конфигурация. При этом лучи, проведённые из общего фокуса зеркал через края сферического зеркала, пройдут через точку сопряжения сферической и плоской частей плоско-сферического зеркала. Для проверки этого вывода с учётом дифракционных явлений, необходимо исследовать влияние величины радиуса апертуры сферической части плоско-сферического зеркала к радиусу апертуры зеркала (k₁ = b/a) на АФР оптического поля при различных значениях радиусов кривизны зеркал (рис. 8):

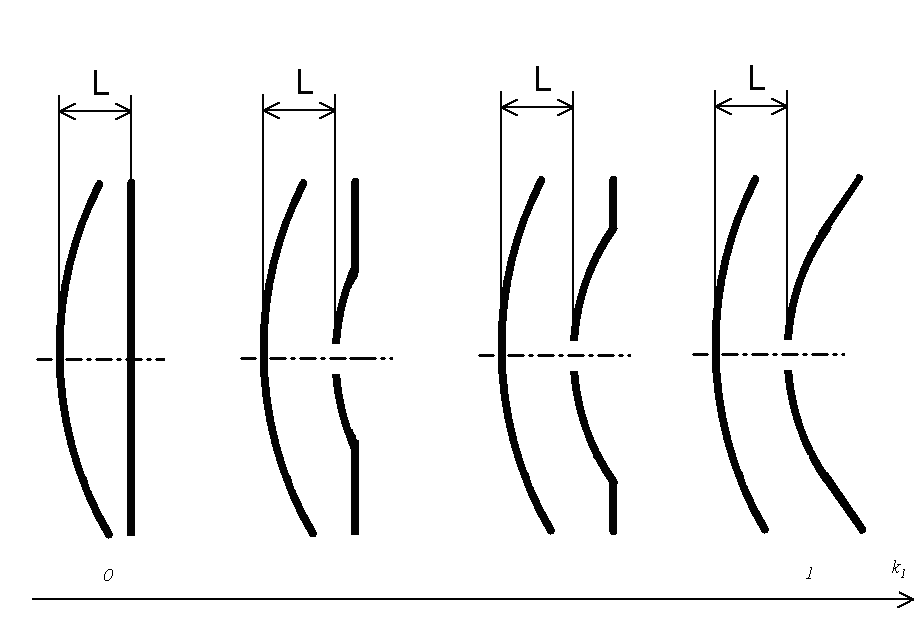
Рис. 8

При исследовании свойств гибридного квазиустойчивого резонатора было установлено, что сходимость итерационного процесса к стационарному решению имеет место не при всех значениях параметров зеркал.

На рис. 9 показана зависимость величины критерия сходимости σ после прохождения 1000 итераций от отношения радиуса апертуры сферической части плоско-сферического зеркала к радиусу апертуры зеркала k₁ при значении коэффициента увеличения неустойчивой части резонатора М = = 1,1:

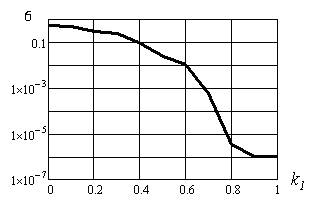
Рис. 9

Видно, что при k₁ меньших 0,8, сходимость решения резко ухудшается. В частности, при k₁ = 0,8 для достижения значения σ = 10^–6 потребовалось выполнить 330 итераций, тогда как при k₁ = 0,2 после проведения 1000 итераций значение σ составило 0,296. Это связано с тем, что резонатор приближается к устойчивой конфигурации и в резонаторе растёт количество колебаний высоких порядков, потери которых малы из-за большого числа Френеля.

На рис. 10 приведены графики зависимости амплитуды поля в точке, соответствующей половине радиуса апертуры зеркала от номера итерации при k₁ = 0,8 (левый график) и k₁ = = 0,2 (правый график):

Рис. 10

Видно, что при малом значении k₁ АФР поля не сходится к стационарному решению. Расчёты показали, что с достаточной точностью можно считать АФР установившимся при σ = 10^–4.

Другой важной характеристикой резонатора является коэффициент равномерности распределения излучения К_исп, который можно определить как

, (67)

где u(t) – АФР поля, нормированное к максимальному значению. В расчётах использовано среднее между значениями К_исп, вычисленными через АФР на левом и правом зеркалах.

На рис. 11 построены расчётные графики зависимости К_исп и α от величины k₁ при М = 1,1:

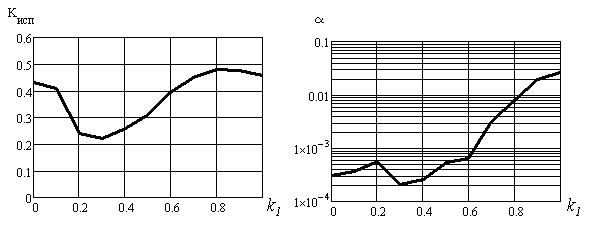
Рис. 11

Рис. 10 и рис. 11 показывают, что оптимальным значением k₁ является значение, обеспечивающее одномодовый режим генерации (σ < 10^-4) и компромисс между величиной потерь и величиной К_исп. Для М = 1,1 таким значением является k₁ = 0,8, при этом значение k₁, соответствующее равноугольной конфигурации составляет 0,9.

Зависимости коэффициента равномерности К_исп (левый столбец графиков), потерь α (средний столбец графиков, логарифмический масштаб по оси ординат) и критерия сходимости σ (правый столбец графиков, логарифмический масштаб по оси ординат) от величины параметра k₁ при М = = 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; приведены на рис. 12а, б, в, г, д, е, ж соответственно.

Рис. 12а

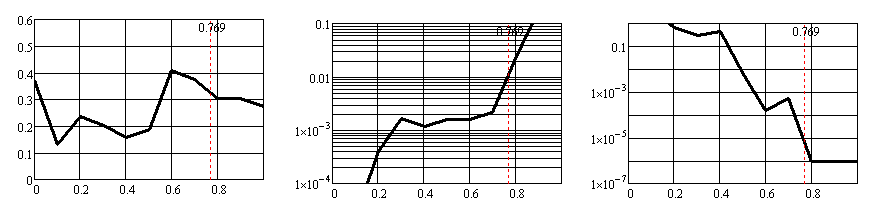
Рис. 12б

Рис. 12в

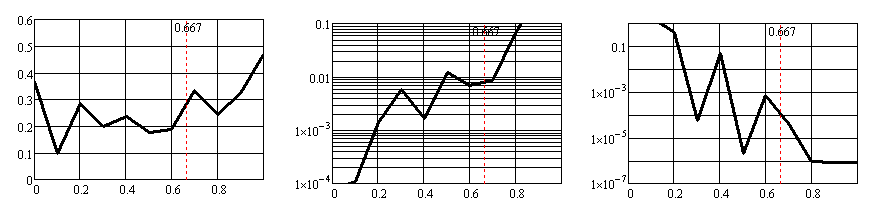
Рис. 12г

Рис. 12д

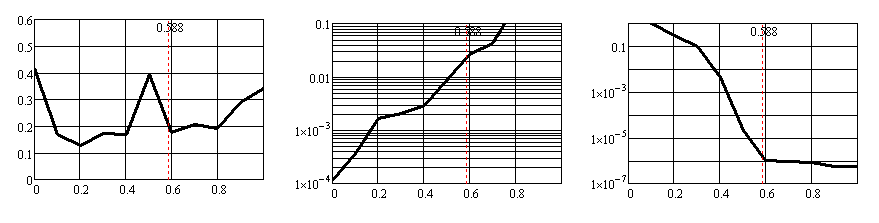
Рис. 12е

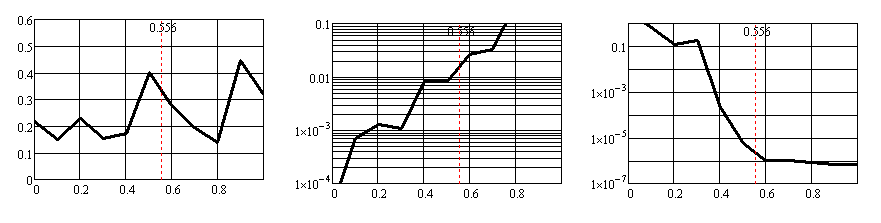
Рис. 12ж

Высокое значение К_исп в одномодовом режиме, составляющее 0,552, достигалось при М = 1,2, когда k₁ = 0,8; величина потерь составила 0,0122. Распределения интенсивности (рис. 13а) и фаз (рис. 13б) оптического поля на левом и правом зеркалах (соответственно левый и правый графики) данного резонатора показаны ниже.

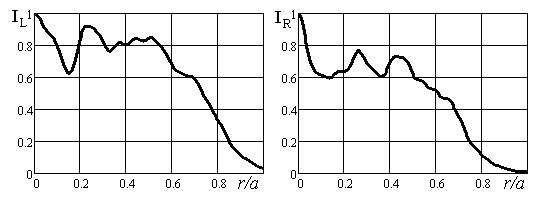
Рис. 13а

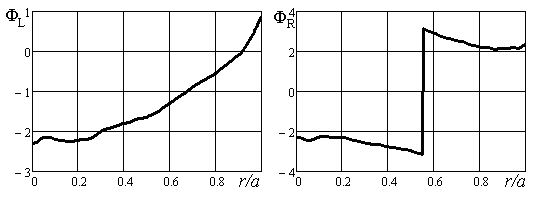
Рис. 13б

Для значений М = 1,2; k₁ = 0,8 исследовались зависимости величины потерь и коэффициента равномерности от отношения радиуса окна для вывода излучения к радиусу апертуры зеркала k₀ при значениях показателя степени сглаживания края окна (μ = 1, 2, 3, 0). Полученные результаты иллюстрируются на рис. 14 (μ = 1), рис. 15 (μ = 2), рис. 16 (μ = = 3) и рис. 17 (μ = 0):

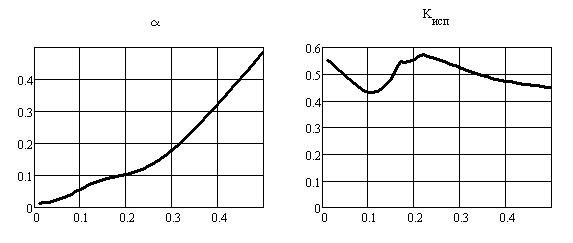
Рис. 14

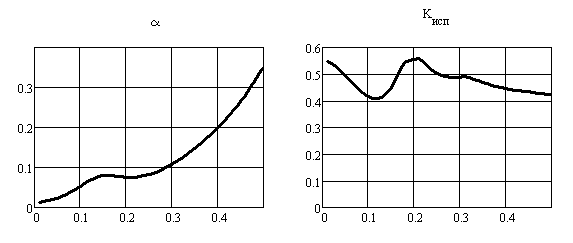
Рис. 15

Рис. 16

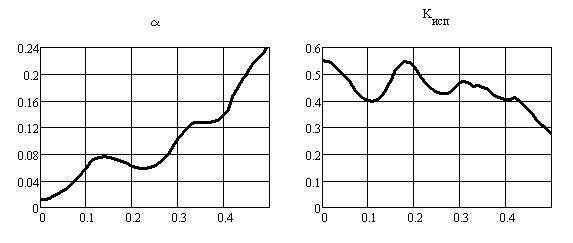
Рис. 17

Из графика зависимости α видно, что при отсутствии сглаживания потери увеличиваются немонотонно. При этом, как следует из графика зависимости К_исп, он также изменяется немонотонно (имеют место локальные минимумы при полуцелых значениях зон Френеля, перекрываемых апертурой окна). При сильном сглаживании края (μ = 1, рис. 14) потери значительно увеличиваются и в зависимости α появляется монотонность, однако зависимость К_исп остаётся немонотонной. При увеличении μ зависимости α и К_исп от радиуса окна приближаются к аналогичным зависимостям, полученным без сглаживания.

Из рассмотрения рис. 14–17 ясно, что наличие окна вносит возмущение в АФР поля в резонаторе, в частности при изменении радиуса окна может уменьшаться величина К_исп. Улучшить ситуацию может применение частично прозрачного материала окна для вывода излучения. Ниже показаны распределения интенсивности поля (рис. 18) на зеркалах резонатора при относительном радиусе окна k₀ = 0.3, Г = 1:

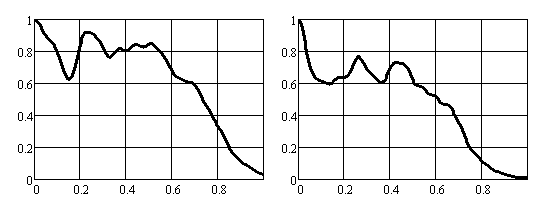
Рис. 18

Видно наличие всплеска интенсивности в центре правого зеркала, ухудшающего равномерность распределения. На рис. 19 показаны зависимости α и К_исп от величины коэффициента пропускания материала окна Г при k₀ = 0.3, μ = 0:

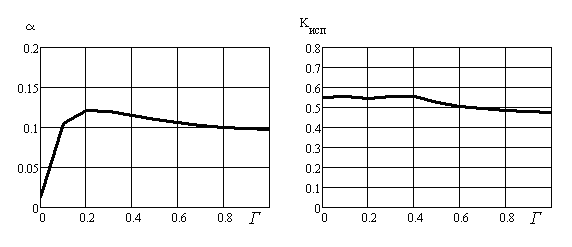
Рис. 19

Из графиков следует, что величина потерь изменяется в пределах 12%, а величина К_исп остаётся практически постоянной при увеличении коэффициента пропускания от 0 до 0,4. На рис. 20 показаны распределения интенсивностей поля при k₀ = 0.3, μ = 0, Г = 0,4:

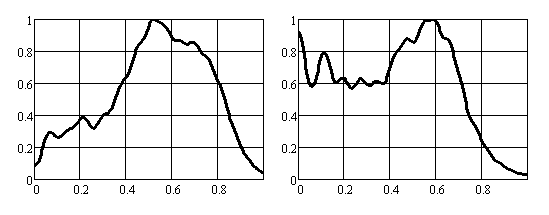
Рис. 20

Можно видеть, что пик интенсивности в центре правого зеркала значительно уменьшился, но появился провал интенсивности в центре левого зеркала. Частично исправить это обстоятельство помогает сглаживание края окна. На рис. 21 показаны распределения интенсивностей поля на зеркалах резонатора при k₀ = 0.3, μ = 1, Г = 0,4:

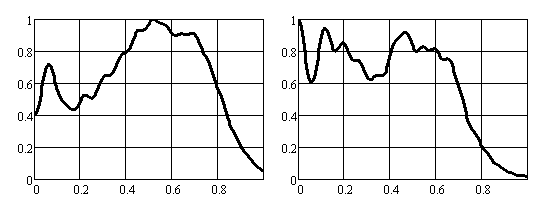
Рис. 21

В последнем случае пик интенсивности на правом зеркале отсутствует, провал интенсивности на левом зеркале значительно уменьшился.

Таким образом, изменяя радиус окна для вывода излучения, коэффициент отражения материала окна и степень сглаживания краёв окна, можно не только управлять величиной потерь на вывод излучения, но и формировать АФР поля в резонаторе, добиваясь максимального значения коэффициента равномерности АФР индуцированного оптического поля.