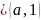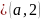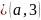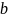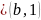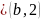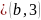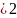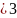- •Введение
- •1. Теория множеств
- •1.1. Основные понятия
- •1.2. Операции над множествами
- •1.3. Алгебраические свойства операций над множествами
- •1.4. Нечёткие множества
- •2. Элементы комбинаторики
- •2.1. Основные правила комбинаторики
- •2.2. Выборки элементов без повторений
- •2.3. Выборки элементов с повторениями
- •2.4. Объединение комбинаторных конфигураций
- •2.5. Бином Ньютона
- •3. Отношения на множествах
- •3.1. Декартово произведение множеств
- •3.2. Булев куб и его свойства
- •3.3. Понятие отношения
- •3.4. Операции над отношениями
- •3.5. Свойства отношений на множестве
- •3.6. Отношения эквивалентности, толерантности и порядка
- •3.7. Нечеткие отношения
- •3.8. Понятие отображения
- •3.9. Алгебраическая операция
- •3.10. Общие сведения об алгебраических системах
- •4 Булевы функции
- •4.1. Основные определения и операции над высказываниями
- •4.2. Типы пф.
- •4.3. Равносильность формул
- •4.4. Дизъюнктивные и конъюнктивные нормальные формы
- •4.5 Алгоритм приведения пф к нормальным формам
- •4.6 Аналитический способ приведения к сднф
- •4.7. Табличный способ приведения к сднф
- •4.8. Табличный способ приведения к скнф
- •4.9. Логическое следствие
- •4.10. Алгоритм проверки правильности рассуждений
- •4.11. Алгоритм определения всех логических следствий из данных посылок
- •4.12. Алгоритм определения всех посылок, логическим следствием которых является данная формула
- •4.13. Полнота систем булевых функций
- •4.14. Полином Жегалкина
- •4.15. Замкнутость
- •4.16. Теорема Поста
- •4.17. Нечеткая логика
- •5. Многозначные функции
- •5.1. Функции и формулы k-значной логики
- •5.2. Полнота и замкнутость функций k-значной логики
- •5.3. Особенности k – значной логики
- •6.. Основные понятия теории графов.
- •6.1. Задачи теории графов.
- •6.2. Основные определения.
- •6.3. Степени вершин графа.
- •6.4. Изоморфизм графов.
- •6.5. Матричные способы задания графов.
- •6.6. Основные операции над графами.
- •6.7. Маршруты в графах
- •6.8. Связность в графах.
- •Связность и матрица смежности графа.
- •6.9. Матрица взаимодостижимости.
- •6.10. Деревья Свободные деревья.
- •Ориентированные, упорядоченные и бинарные деревья.
- •6.11. Эйлеровы графы.
- •6.12 Гамильтоновы графы.
- •6.13. Планарные графы.
- •6.14. Потоки в сетях. Основные определения.
- •Теорема Форда и Фалкерсона.
- •Алгоритм построения максимального потока в сети.
- •7. Конечные автоматы
- •7.1. Понятие конечного автомата Общие сведения о конечных автоматах
- •7.2. Абстрактное определение конечного автомата
- •7.3. Автоматная функция и её моделирование Понятие ограниченно детерминированной функции
- •Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •7.4. Эксперименты с автоматами
- •8. Рекуррентные уравнения
- •8.1. Определение рекуррентного уравнения/ Решение линейного однородного рекуррентного уравнения
- •8.2. Решение линейного неоднородного рекуррентного уравнения
- •8.3. Решение рекуррентного уравнения для чисел Фибоначчи
- •Заключение
- •Библиографический список
- •Оглавление
- •1.Теория множеств 5
- •2 Элементы комбинаторики 14
- •3 Отношения на множествах 22
- •4. Булевы функции 42
- •5. Многозначные функции 64
- •6. Основные понятия теории графов 70
- •7. Конечные автоматы 106
- •8. Рекуррентные уравнения 120
- •394026 Воронеж, Московский просп., 14
3. Отношения на множествах
3.1. Декартово произведение множеств
При задании конечных множеств не имеет значения порядок, в котором перечислены его элементы. Однако бывают случаи, когда необходимо работать с упорядоченными наборами элементов. Для этого необходимо познакомимся с упорядоченной парой элементов.
Упорядоченной
парой называется запись вида
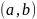 ,
где на первом месте расположен элемент
а,
принадлежащий некоторому множеству А,
а на втором месте – элемент
,
где на первом месте расположен элемент
а,
принадлежащий некоторому множеству А,
а на втором месте – элемент
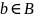 .
В частном случае множества А
и В
могут совпадать.
.
В частном случае множества А
и В
могут совпадать.
Множество
всех упорядоченных наборов элементов
вида
таких, что
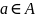 и
называется декартовым
или прямым
произведением
множеств А
и В
и обозначается как
.
Следовательно, по определению:
и
называется декартовым
или прямым
произведением
множеств А
и В
и обозначается как
.
Следовательно, по определению:
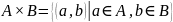 .
.
Пример.
Пусть
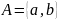 и
и
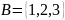 .
Тогда:
.
Тогда:
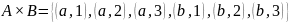 ;
;
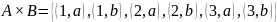 .
.
Заметим,
что при этом
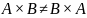 .
Далее
.
Далее
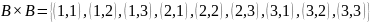 .
.
Отметим,
что если множества А
и В
конечны и
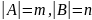 ,
то
,
то
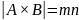 .
.
Прямое произведение множеств может быть изображено графически. Для этого используется диаграмма Венна. В частности, для множества из предыдущего примера она имеет вид
Таблица 5
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
В
качестве следующего примера рассмотрим
произведение множества вещественных
чисел R
на самого на себя. Множество
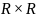 или
или
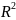 состоит из всех упорядоченных пар
вещественных чисел
состоит из всех упорядоченных пар
вещественных чисел
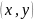 .
Их можно представить себе как координаты
точек на плоскости. Множество
называется декартовой
плоскостью.
.
Их можно представить себе как координаты
точек на плоскости. Множество
называется декартовой
плоскостью.
Декартовым
произведением произвольного числа
множеств
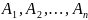 называется множество
называется множество
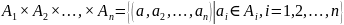 .
.
Элементы этого множества – конечные упорядоченные наборы, с которыми работают все языки программирования и базы данных.
Если
каждое из множеств
совпадает со множеством А,
то прямое произведение данного множества
самого на себя,
взятое
раз называется
степенью
множества А
и записывается
в виде
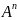 то есть
то есть
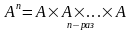 .
.
Пример.
Пусть
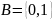 .
Тогда множество
.
Тогда множество
 состоит из всевозможных последовательностей
нулей и единиц длины n.
Такая последовательность называется
булевым
вектором (битовой строкой или строкой
бит) длины
n.
Совокупность всех булевых векторов
размерности n
называется
булевым кубом размерностью.
состоит из всевозможных последовательностей
нулей и единиц длины n.
Такая последовательность называется
булевым
вектором (битовой строкой или строкой
бит) длины
n.
Совокупность всех булевых векторов
размерности n
называется
булевым кубом размерностью.

 a
a