
- •Введение
- •1. Теория множеств
- •1.1. Основные понятия
- •1.2. Операции над множествами
- •1.3. Алгебраические свойства операций над множествами
- •1.4. Нечёткие множества
- •2. Элементы комбинаторики
- •2.1. Основные правила комбинаторики
- •2.2. Выборки элементов без повторений
- •2.3. Выборки элементов с повторениями
- •2.4. Объединение комбинаторных конфигураций
- •2.5. Бином Ньютона
- •3. Отношения на множествах
- •3.1. Декартово произведение множеств
- •3.2. Булев куб и его свойства
- •3.3. Понятие отношения
- •3.4. Операции над отношениями
- •3.5. Свойства отношений на множестве
- •3.6. Отношения эквивалентности, толерантности и порядка
- •3.7. Нечеткие отношения
- •3.8. Понятие отображения
- •3.9. Алгебраическая операция
- •3.10. Общие сведения об алгебраических системах
- •4 Булевы функции
- •4.1. Основные определения и операции над высказываниями
- •4.2. Типы пф.
- •4.3. Равносильность формул
- •4.4. Дизъюнктивные и конъюнктивные нормальные формы
- •4.5 Алгоритм приведения пф к нормальным формам
- •4.6 Аналитический способ приведения к сднф
- •4.7. Табличный способ приведения к сднф
- •4.8. Табличный способ приведения к скнф
- •4.9. Логическое следствие
- •4.10. Алгоритм проверки правильности рассуждений
- •4.11. Алгоритм определения всех логических следствий из данных посылок
- •4.12. Алгоритм определения всех посылок, логическим следствием которых является данная формула
- •4.13. Полнота систем булевых функций
- •4.14. Полином Жегалкина
- •4.15. Замкнутость
- •4.16. Теорема Поста
- •4.17. Нечеткая логика
- •5. Многозначные функции
- •5.1. Функции и формулы k-значной логики
- •5.2. Полнота и замкнутость функций k-значной логики
- •5.3. Особенности k – значной логики
- •6.. Основные понятия теории графов.
- •6.1. Задачи теории графов.
- •6.2. Основные определения.
- •6.3. Степени вершин графа.
- •6.4. Изоморфизм графов.
- •6.5. Матричные способы задания графов.
- •6.6. Основные операции над графами.
- •6.7. Маршруты в графах
- •6.8. Связность в графах.
- •Связность и матрица смежности графа.
- •6.9. Матрица взаимодостижимости.
- •6.10. Деревья Свободные деревья.
- •Ориентированные, упорядоченные и бинарные деревья.
- •6.11. Эйлеровы графы.
- •6.12 Гамильтоновы графы.
- •6.13. Планарные графы.
- •6.14. Потоки в сетях. Основные определения.
- •Теорема Форда и Фалкерсона.
- •Алгоритм построения максимального потока в сети.
- •7. Конечные автоматы
- •7.1. Понятие конечного автомата Общие сведения о конечных автоматах
- •7.2. Абстрактное определение конечного автомата
- •7.3. Автоматная функция и её моделирование Понятие ограниченно детерминированной функции
- •Моделирование автоматной функции с помощью схемы из функциональных элементов и задержки
- •7.4. Эксперименты с автоматами
- •8. Рекуррентные уравнения
- •8.1. Определение рекуррентного уравнения/ Решение линейного однородного рекуррентного уравнения
- •8.2. Решение линейного неоднородного рекуррентного уравнения
- •8.3. Решение рекуррентного уравнения для чисел Фибоначчи
- •Заключение
- •Библиографический список
- •Оглавление
- •1.Теория множеств 5
- •2 Элементы комбинаторики 14
- •3 Отношения на множествах 22
- •4. Булевы функции 42
- •5. Многозначные функции 64
- •6. Основные понятия теории графов 70
- •7. Конечные автоматы 106
- •8. Рекуррентные уравнения 120
- •394026 Воронеж, Московский просп., 14
2. Элементы комбинаторики
2.1. Основные правила комбинаторики
Комбинаторика – раздел математики, связанный с решением задач выбора и размещения элементов конечного множества в соответствии с заданными правилами.
Каждое правило определяет способ построения некоторой конструкции из элементов исходного множества. Полученные конструкции называются комбинаторными конфигурациями.
Цель комбинаторного анализа заключается в изучении комбинаторных конфигураций, алгоритмов их построения, а также решении задач по их перечислению.
Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения.
Правило суммы. Пусть A, B – конечные множества, |A| = n, |B| = m.
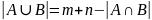 ,
,
следовательно
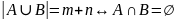 .
.
Комбинированная интерпретация.
Если некоторый объект A можно выбрать n способами, а другой объект B можно выбрать m способами, то выбор "либо A, либо B" можно осуществить n+m способами.
Правило
произведения.
Если мощность |A|
= n,
|B|
= m,
то
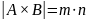 .
.
Комбинаторная интерпретация.
Если
объект A
можно выбрать n
способами,
а после каждого такого выбора другой
объект B
можно выбрать
(независимо от выбора объекта A)
m
способами,
то пары объектов A
и B
можно выбрать
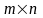 способами.
способами.
Пусть
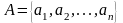 ,
,
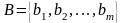 и |А|
- число элементов множества A.
Составим декартово произведение
и |А|
- число элементов множества A.
Составим декартово произведение
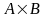 множеств
A
и B,
т.е. множество пар
множеств
A
и B,
т.е. множество пар
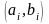 .
.
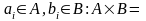
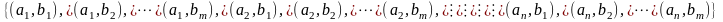
Тогда правило произведения записывается следующим образом:
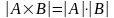
Пример. Сколько всего существует двузначных чисел?
Решение.
Поскольку в двузначном числе цифра,
обозначающая
число десятков, должна быть отлична от
нуля, то A
= {1, 2, ..., 9}, B
= {0, 1, 2, ..., 9} и
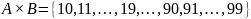 ,
,
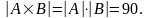
2.2. Выборки элементов без повторений
Простейшими комбинаторными конфигурациями являются перестановки, размещения и сочетания.
Перестановки.
Пусть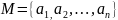 .
Перестановкой элементов множества M
называется любой упорядоченный набор
элементов
.
Перестановкой элементов множества M
называется любой упорядоченный набор
элементов
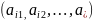 ,
состоящий из n
различных элементов множества M.
,
состоящий из n
различных элементов множества M.
Перестановки отличаются друг от друга порядком следования элементов.
Теорема. Число всех перестановок равно n!
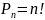
Доказательство. На первом месте можно разместить n элементов, на втором – любой из оставшихся (n-1) элементов и т.д. Для последнего места остается 1 элемент. В силу правила произведения имеем:
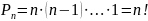 .
.
Пример. Сколькими способами можно разместить 5 студентов при наличии 5 мест.
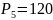 .
.
Размещения.
Пусть
множество M
состоит из
n
элементов. Размещением (упорядоченной
выборкой) из n
элементов
по m
элементов
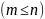 называется любой упорядоченный набор
элементов
,
состоящий из m
различных
элементов множества M.
называется любой упорядоченный набор
элементов
,
состоящий из m
различных
элементов множества M.
Теорема.
Число размещений n
элементов по m
элементов
обозначается .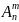 .
Справедлива формула:
.
Справедлива формула:
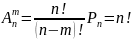
Доказательство. Размещение M элементов множества Mможно представить, как заполнение некоторых m позиций элементами множества M. При этом первую позицию можно заполнить nспособами, вторую позицию (n-1) способами. Последнюю позицию можно заполнить (n-m+1) способами.
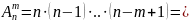
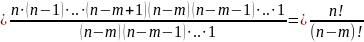
Пример. Из 10 книг производным образом берутся 3 книги и ставятся на полку. Сколько существует способов такой расстановки книг.
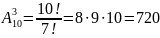 .
.
Заметим, что размещение из n элементов по n элементам представляет собой перестановку, т.е.:
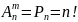
Сочетания.
Сочетанием
(неупорядоченной выборкой) из n
элементов
по m,
где
![]() ,
называется неупорядоченное подмножество
множества M,
состоящее из n
различных
элементов.
,
называется неупорядоченное подмножество
множества M,
состоящее из n
различных
элементов.
Теорема.
Число сочетаний из n
элементов
по m
обозначается как
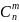 и определяется по формуле:
и определяется по формуле:
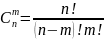
Доказательство.
Если объединить размещения из n
элементов
по m,
которые состоят из одних и тех же
элементов (то есть не учитывать порядка
расположения элементов), то получим
сочетание из n
элементов
по m.
Так как для каждого такого сочетания
можно получить n!
размещений. Тогда
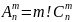 и, следовательно:
и, следовательно:
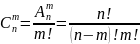 .
.
