5. Системы счисления и арифметические операции над числами

1. Системы счисления для представления чисел в ЭВМ

2. Представление в ЭВМ целых двоичных чисел без знака

3. Представление в ЭВМ целых чисел со знаком

4. Двоично-десятичная система представления чисел

5. Представление чисел в формате с плавающей точкой

Для внутреннего представления целых и десятичных чисел со знаком и без знака в ЭВМ используются двоичные числа. При этом числа, в зависимости от способа кодирования, представляются в различных форматах и занимают несколько байтов. Для записи чисел в программах также используются числа в различных системах счисления.

Цель главы – ознакомление с основными системами счисления, основными методами представления в ЭВМ целых чисел со знаком и без него и представлением чисел в формате с плавающей точкой.

После изучения главы необходимо знать

• Используемые системы счисления для представления чисел,

• представление целых чисел без знака,

• представление целых чисел со знаком в прямом коде,

• представление целых чисел со знаком в обратном коде,

• представление целых чисел со знаком в двоично-десятичном коде,

• представление дробных чисел со знаком в формате с плавающей точкой.

5.1. Системы счисления для представления чисел в эвм

Общепринятой формой представления чисел является использование позиционной системы счисления. В позиционной системе счисления вес, т.е. значимость каждой цифры a_i , составляющей число, определяется его позицией внутри числа. В соответствии со своей позицией каждая цифра a_i числа N умножается на коэффициент, представляющий собой так называемое основание системы счисления p, возведенное в степень, равную номеру позиции данной цифры справа налево.

N = ..a₄ a₃ a₂ a₁ a₀ ..=..a₄ p⁴ +a₃ p³ +a₂ p² +a₁ p¹ +a₀ p⁰.. ( 5.1)

Внутри машины все числа представляются в системе счисления с основанием 2. Такие числа записываются в виде последовательности 0 и 1 и называются двоичными. Для удобства ввода/вывода и при составлении программ в ряде случаев используется системы счисления с основанием 8 (восьмеричная) и 16 (шестнадцатеричная), позволяющие легко преобразовывать записанные в них числа в двоичные. В шестнадцатеричной системе счисления для обозначения цифр более 9 используются буквы: 10 =А, 11 =В, 12 =С, 13 =D, 14 =Е, 15 =F. Для указания системы счисления часто используют нижний индекс, который показывает основание системы счисления. Для указания, что число записано в 16-ричной системе счисления, в его конце вместо нижнего индекса часто ставят букву h: 1АВ2h.

Примеры:

5724₁₀=5*10³+7*10²+2*10¹+4*10⁰ - целое число в десятичной системе счисления;

34,85₁₀=3*10¹+4*10⁰+8*10^-1+5*10^-2-дробное число в десятичной системе счисления;

2731₈ =2*8³ +7*8² +3*8¹ +1*8⁰ - целое число в восьмеричной системе счисления;

11010₂ =1*2⁴ +1*2³ +0*2² + 1*2¹ +0*2⁰ - целое число в двоичной системе счисления.

Десятичное значение числа находится путем преобразования каждой его цифры в десятичный эквивалент и выполнения действий десятичной арифметики в соответствии с формулой ( 5.1 ). Например:

1ВЕ8h =1х16 ³+11х16² +14х16¹ +8х16⁰ =7144₁₀

437.5₈ =4х8² +3х8¹ +7х8⁰ +5х8^-1 =287.625₁₀

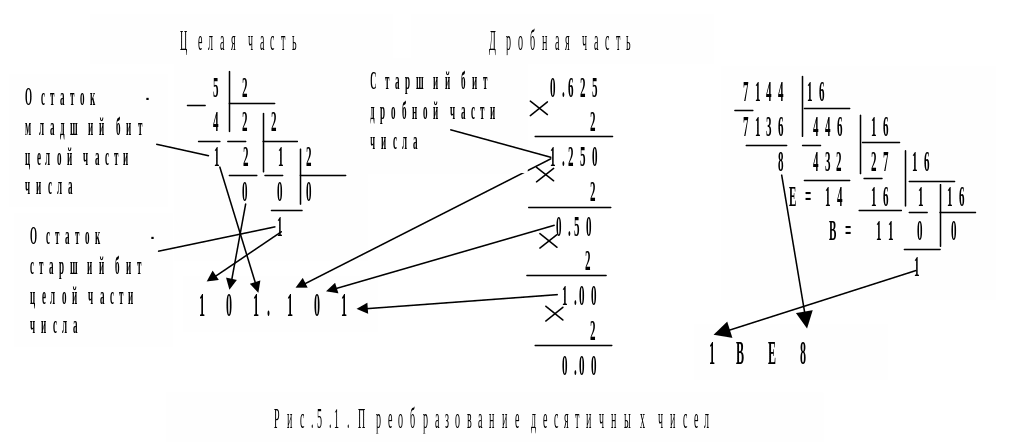
Для получения числа с другим основанием счисления из десятичного целого последовательно делят исходное число на новое основание и записывают последовательно остатки справа налево как цифры целой части числа. Для преобразования дробной части десятичного числа к новому основанию дробные части числа умножают последовательно на новое основание счисления, приписывая последовательно слева направо получаемые целые части как цифры дробной части числа по новому основанию (рис.5.1).

Примеры: 5.625 =101.101 =2² +2⁰ +2^-1 +2^-3 =5.625

7144₁₀ = 1х16³ +11х16² +14х16¹ +8х16⁰ =1ВЕ8₁₆=1ВЕ8h

Для преобразования двоичного числа в восьмеричное (шестнадцатеричное), оно, начиная от двоичной точки, двигаясь влево и вправо, разбивается на группы из 3(4) бит и каждая группа заменяется соответствующей восьмеричной (шестнадцатеричной) цифрой.

Целые числа

101011000110 ₂=101 011 000 110 =5306

101011000110 ₂=1010 1100 0110 =АС6

Дробные числа

11.1010011011₂ =011.101 001 101 100 =3.5154

11.1010011011 ₂=0011.1010 0110 1100 =3.А6С

При обратных преобразованиях каждая восьмеричная (шестнадцатеричная) цифра заменяется двоичным 3-х(4-х)-разрядным числом. Напомним, что разряды двоичного числа обычно называются битами, восемь следующих подряд битов составляют байт, а два байта - слово.

разряды (биты)

1 0 0 1 1 1 0 0 1 0 1 0 0 0 1 0

¦<-- старший -->¦<--- младший -->¦ - байты

¦<---------- слово -------------->¦

Рис.5.2. Формат машинного слова