
- •Введение
- •1. Сведения из теории вероятностей
- •Значение статистических методов исследования
- •1.2. Экспериментальные основы теории вероятностей
- •1.3. Вероятность события. Свойства вероятности событий
- •1.4 Соединения или комбинации
- •1.4.1. Размещения и перестановки
- •1.4.2. Соединения и выборки
- •1.4.3. Сочетания
- •1.4.4. Задачи о размещении элементов по ячейкам.
- •2. Распределения вероятностей
- •2.1. Биномиальное распределение
- •2.2. Гипергеометрическое распределение
- •2.3. Расчеты вероятностей числа дефектных изделий в выборке
- •2.4. Функция распределения и плотность вероятности случайной величины
- •2.5. Распределение Пуассона.
- •2.5.1. Применение распределения Пуассона в задачах качества
- •2.6. Показательное распределение времени ожидания сбоя
- •2.6.1. Функция надежности.
- •2.6.2. Функция распределения времени ожидания сбоя.
- •2.6.3. Метод дополнительной вероятности.
- •2.6.4. Зависимость интенсивности отказов от времени. Практические случаи - кривая в форме «ванны».
- •2.6.5. Среднее время между отказами
- •2.7. Нормальный закон распределение и его приложения в задачах качества
- •2.7.1. Нормальная плотность вероятности и ее параметры.
- •2.7.2. Функция Лапласа и расчеты вероятностей при нормальном распределении
- •Значение функции
- •2.7.3. Возможность (осуществимость) процесса.
- •2.7.4. Статистическое управление качеством (процессами).
- •3. Статистическая выборка [7]
- •3.1. Выборочный контроль и оперативная характеристика.
- •3.2. Планы выборочного контроля
- •Планы типа однократной выборки
- •Планы типа двукратной (многократной) выборки
- •Планы типа последовательного анализа
- •3.3. Оперативная характеристика
- •3.4. Методы выборочного контроля
- •3.5. Программы выборки на основе риска производителя
- •3.6. Программы выборки на основе риска потребителя
- •Процент брака
- •3.7. Соотношение между различными программами выборки
- •3.8. Решение задач с использованием таблиц выборочного контроля
- •3.9. Общие требования, предъявляемые к стандартам выборочного контроля
- •4. Контрольные карты статистически управляемых процессов [7]
- •4.1. Примеры построения контрольных карт
- •4.1.1. Карта динамики процесса
- •4.1.2. Карта (диаграмма) управляемости процесса
- •4.2. Методика выбора формы контрольной карты
- •4.3. Контрольная карта числа дефектных единиц продукции .(np – карта)
- •4.4. Контрольная карта числа дефектов (с-карта)
- •4.5. Сигнальные признаки. Предельные отклонения
- •Сигнальные отклонения
- •Дополнительные признаки
- •5. Контрольные карты количественных и интегрально-суммарных признаков [7]
- •5.1. Вычисление предельных отклонений для нормального закона распределения
- •5.2. Контрольные карты для средних арифметических значений и размахов: и r
- •5.3. Диапазон как замена стандартного отклонения
- •Задание № 1 для самостоятельной работы
- •Алгоритм построения контрольных карт и r
- •Задание № 2 для самостоятельной работы
- •Сигнальные отклонения
- •5.4. Интегрально-суммарные контрольные карты
- •5.3. Интегрально-суммарная карта,
- •6. Cтатистические методы анализа динамических рядов [7]
- •6.1. Метод скользящей средней
- •6.2. Метод взвешенной скользящей средней
- •394026 Воронеж, Московский просп., 14
2.7.2. Функция Лапласа и расчеты вероятностей при нормальном распределении
Для
определения вероятности
![]()
н![]() ахождения
в интервале случайной
величины
ахождения
в интервале случайной
величины
![]() ,
следующей
нормальному закону, приходится вычислять
определенный
интеграл вида
,
следующей
нормальному закону, приходится вычислять
определенный
интеграл вида
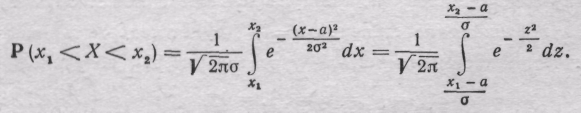
Определенный интеграл с переменным верхним пределом вида
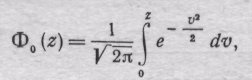
выражающий
площадь под кривой
![]() в
промежутке от 0 до
в
промежутке от 0 до
![]() (рис.
2.9), носит название нормированной
функции Лапласа, или
просто функции
Лапласа.
(рис.
2.9), носит название нормированной
функции Лапласа, или
просто функции
Лапласа.

Рис. 2.9
В таблицах (см. табл. 2.4) обычно приведены значения функции Лапласа для z от 0 до 5.
Таблица 2.4
Значение функции
![]()

Заметим, что
![]()
![]()
и
![]()
т. е.
площадь в промежутке
![]() равна
площади в промежутке
равна
площади в промежутке
![]() ,
но считается отрицательной.
,
но считается отрицательной.
Интегральную функцию нормального распределения можно выразить через функцию Лапласа следующим образом:
![]()
Если теперь воспользоваться функцией Лапласа, то
получим
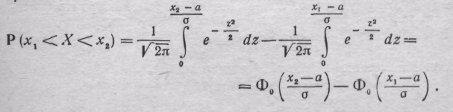
Полезно помнить,
что для нормально распределенной
случайной величины вероятность оказаться
в полосе
![]() от
среднего равна 68%, вероятность выхода
за пределы полосы
от
среднего равна 68%, вероятность выхода
за пределы полосы
![]() составляет
приблизительно 5% ,и только в 0.27% случаев
процесс может выйти за пределы
составляет
приблизительно 5% ,и только в 0.27% случаев
процесс может выйти за пределы
![]() .
.
Пример.
1. Определить вероятность получения 16 или менее бракованных деталей в выборке из 100 изделий, если доля брака во всей партии составляет 10% (0.1).
*
Используем биномиальное распределение
:
![]() ,
,
![]() .
.
Табл. 2.1. дает
значение
![]() ,
нас интересует дополнительная вероятность
,
нас интересует дополнительная вероятность
![]() .
.
* Используем
пуассоновское распределение как
аппроксимацию биномиального:
![]() .
.
Табл.2.2. дает
значение
![]() ,
,
дополнительная
вероятность
![]() .
.
Используем
нормальное распределение как
аппроксимацию биномиального:
![]() ,
,
![]() ;
;
условие, что
![]() означает,
что приведенная величина
означает,
что приведенная величина
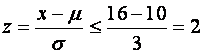 .
.
Вероятность
![]()
![]()
![]()
![]() 0,5+
0,5+
![]() =
=
=0,5+
![]() =0,9773
=0,9773
В данном случае для аппроксимации биномиального распределения предпочтительнее использовать нормальный закон.
2.7.3. Возможность (осуществимость) процесса.
Представим себе, что имеется станок, предназначенный для изготовления деталей с определенными отклонениями. Процесс протекает в нормальных условиях, выполняется ряд измерений изготавливаемых на нем деталей. Распределение измеряемых параметров будет характеризовать «возможность процесса», выполняемого на станке. Если допуски на размеры конкретной детали шире, чем погрешность процесса, то станок обеспечивает необходимую возможность процесса. Ели же допуски уже, чем погрешность процесса - возможность выполнения процесса на данном станке не обеспечивается и данную работу на нем не следует выполнять.
Необходимо отметить, что возможность процесса выясняется не только по ряду измерений, выполняемых при статистическом анализе. Предположение о нормальном законе распределения вероятностей допускает выход измеряемых параметров за пределы того диапазона, который должен быть обеспечен.
В управлении
качеством границы
![]() являются
предельными для осуществимого процесса.
являются
предельными для осуществимого процесса.
Соответственно определяется индекс возможности процесса -
![]() ,
,
где ВО и НО суть верхнее и нижнее предельные отклонения, заданные техническими условиями.
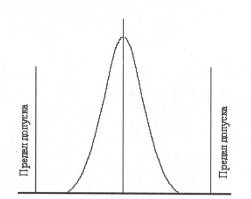
Рис . 2.10. Процесс имеет большой запас
в отношении пределов допуска
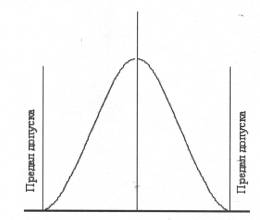
Рис. 2.11. Процесс проходит точно в пределах допуска
На рис.2.10 - рис.2.13 представлены нормальные кривые с различным расположением по отношению к пределам допусков, и приводится их интерпретация.
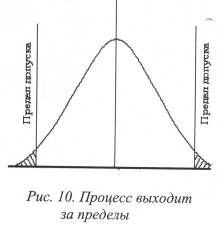
Рис.2.12

Рис. 2.13
На рис. 2.10 представлена ситуация, когда технологический процесс может обеспечить выпуск продукции в пределах технических условий со значительным запасом. Это значит, что он может осуществляться с помощью менее точных, а следовательно, как правило, менее дорогостоящих станков или технологического оборудования. На рис. 2.11 показана ситуация, когда процесс точно укладывается в пределы, но в этом случае почти наверняка будет производиться брак, списываемый в лом, поскольку, как это показано на рис.2.12., весьма вероятно, что процесс налажен неточно вокруг центральной точки или отклоняется от нее (рис.2.13).
Данная проблема может решаться следующими способами:
* путем усовершенствования процесса или использования лучших станков или операторов;
* путем расширения пределов допусков технических условий;
* путем признания неизбежности производства некоторого количества брака;
* путем оценки этого количества брака и обеспечения дополнительного контроля для его разбраковки.
