2.5.1. Применение распределения Пуассона в задачах качества
Биномиальный закон
распределения относится к случаям,
когда была сделана выборка фиксированного
объема. Распределение Пуассона относится
к случаям, когда число случайных событий
происходит на определенных длинах,
площадях, объемах или временах, при этом
определяющим параметром распределения
является среднее число событий
,
а не объем выборки
и
вероятность успеха
.
Распределение вероятностей для числа
успехов
имеет
при этом следующий вид:
.
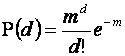Здесь е - основание натуральных логарифмов, это иррациональное число, равно 2.718281… .
Закон Пуассона распространяется на “редко” происходящие события. При этом возможность очередной “удачи” (например, сбоя) является постоянной. Сохраняется непрерывно и не зависит от числа предыдущих “удач” или ”неудач (это называют “независимостью от прошлого”).
Для приложений
важным свойством распределения Пуассона
является также то, что оно аппроксимирует
биномиальное распределение в пределе,
когда
,
а
так,
что среднее
.
Таким образом,
для эффективного применения распределения
Пуассона как аппроксимации биномиального
необходимо, чтобы вероятность успеха
была
существенно меньше
,
а произведение
была
порядка единицы и более.
Учитывая указанное предельное свойство, нетрудно получить выражение дисперсии для пуассоновской случайной величины как соответствующий предел дисперсии биномиального распределения,
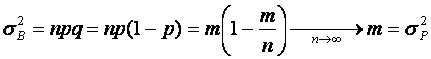
Таким образом,
для пуассоновской случайной величины
математическое ожидание
и дисперсия
имеют
одно и то же значение равное
.
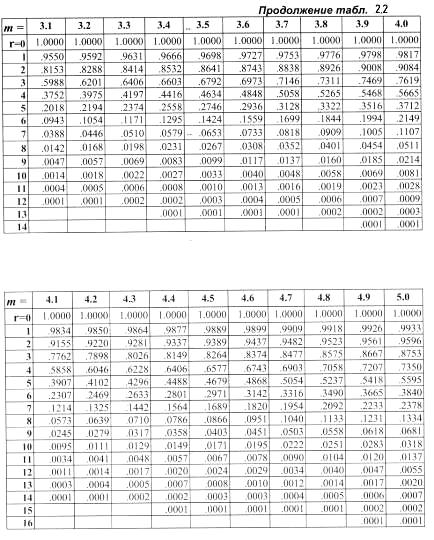
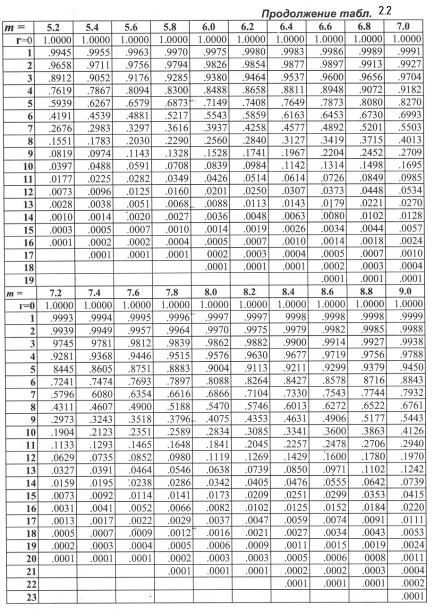
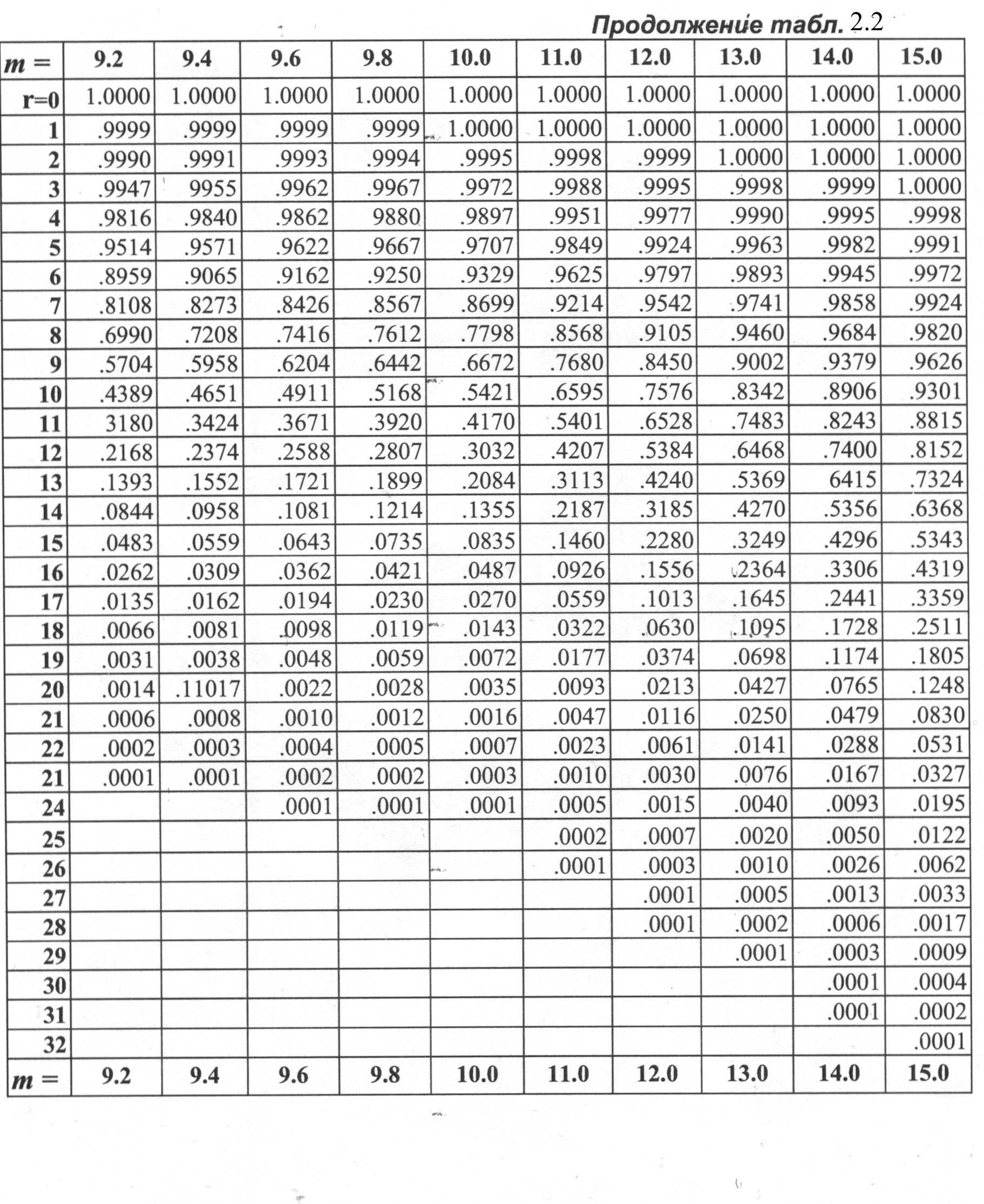
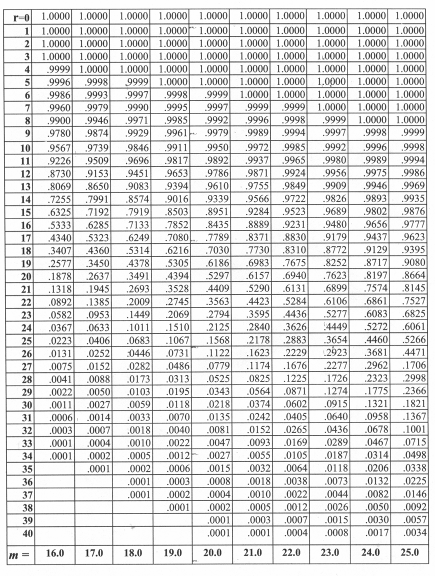
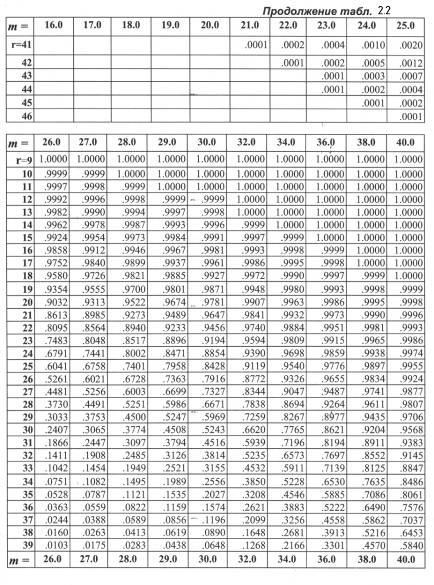
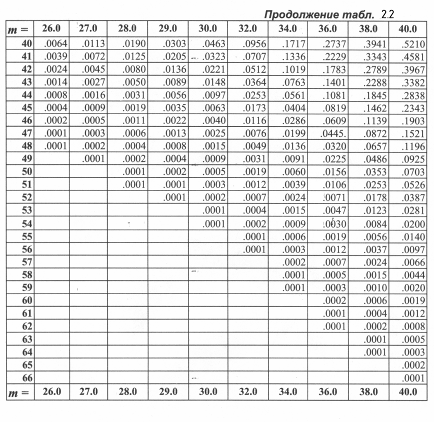
В таблице 2.2. представлены кумулятивные пуассоновские вероятности. как в таблице 2.1 для биномиального распределения
.
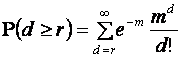Правила использования таблицы 2.2 такие же, как и таблицы 2.1..
Примеры
1. Какова вероятность получения двух бракованных изделий в выборке из 20 штук, если вероятность брака для процесса составляет 0,04 (4%)?
Применить закон распределения Пуассона для этого случая. Какова будет вероятность того, что произойдет в точности два отказа, если пользоваться таблицей для закона Пуассона.
Среднее число
отказов в выборке из
,
при вероятности отказа
,
равно
.
В столбце, соответствующем
,
и в строках для
и
находим
значения кумулятивных вероятностей
и
.
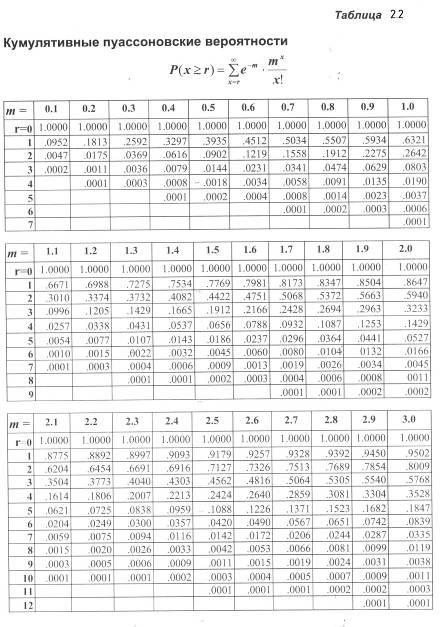
Их разность даст искомый ответ,
.
Сравните этот результат с ранее полученным ответом - 0.1458.
2. В течение дня 144 текстильные машины, производящие пряжу одного и того же типа, имели 216 остановок. Какова вероятность того, что одна машина в течение одного дня будет иметь 4 или более остановок?
В условии неявно предполагается, что причина остановки станка мгновенно определяется, устраняется, и он вновь включается в работу (см. ниже “момент восстановления”). В такой ситуации биномиальное распределение неприменимо, и мы должны воспользоваться распределением Пуассона.
Среднее число
остановок на одну машину в день составляет
216/144 = 1.5. Итак, для использования Таблицы
3.2. мы имеем m = 1.5,
.
Ответом является вероятность, равная 0.0656.