3.6. Ранг матрицы. Базисный минор.

Рассмотрим некоторую, не обязательно квадратную, матрицу А. Выберем какие-нибудь s номеров строк i₁, i₂, , i_s и s номеров столбцов j₁, j₂, , j_s, причём i₁<i₂<<i_s и j₁<j₂<<j_s.

Определение. Минором порядка s матрицы А называется детерминант матрицы порядка s, образованный элементами, расположенными на пересечении выбранных строк и столбцов, т.е. число

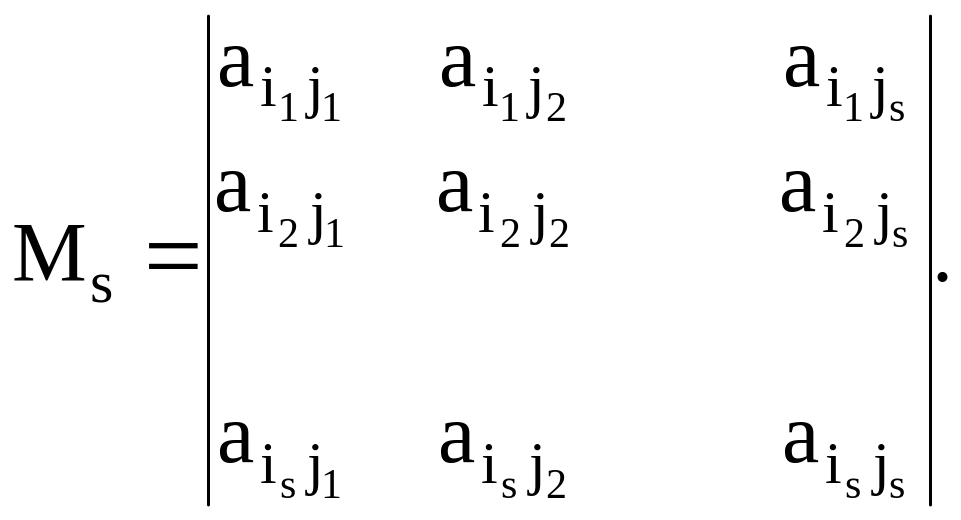
Определение. В матрице А размеров минор порядка r называется базисным, если он отличен от нуля, а все миноры порядка r+1 равны нулю или миноров порядка r+1 вообще нет, т.е. r совпадает с меньшим из чисел m или n.

Определение. Строки и столбцы, на пересечении которых расположен базисный минор, называются базисными строками и столбцами.

Определение. Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы и обозначается .

Свойства ранга матрицы и базисного минора.

1. Ранг матрицы А размеров 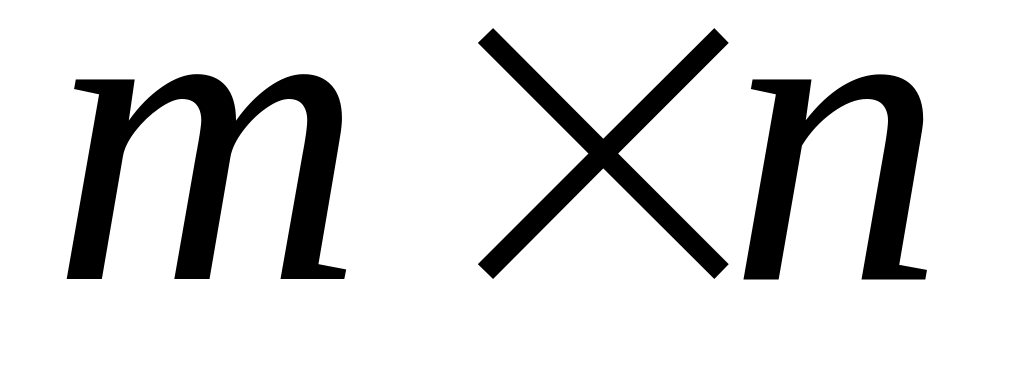не превосходит меньшего из её размеров.

2. rangA=0 тогда и только тогда, когда

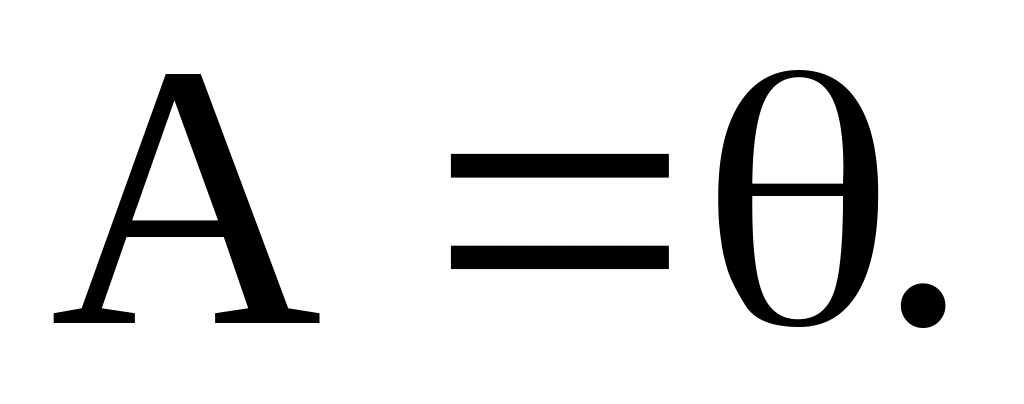
3. Для квадратной матрицы А порядка n rangA= n тогда и только тогда, когда А – невырожденная.

4. Базисные строки (столбцы) матрицы А линейно независимы.

5. Теорема о базисном миноре. В произвольной матрице каждый столбец (строка) является линейной комбинацией базисных столбцов (строк).

6. Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (строк) в этой матрице.

7. 

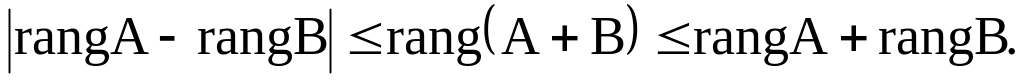
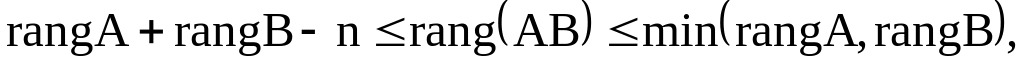8. где n – число столбцов матрицы А или строк матрицы B.

9. rang(A^TA)=rang A.

10. rang(AB)= rang A, если B – квадратная матрица и

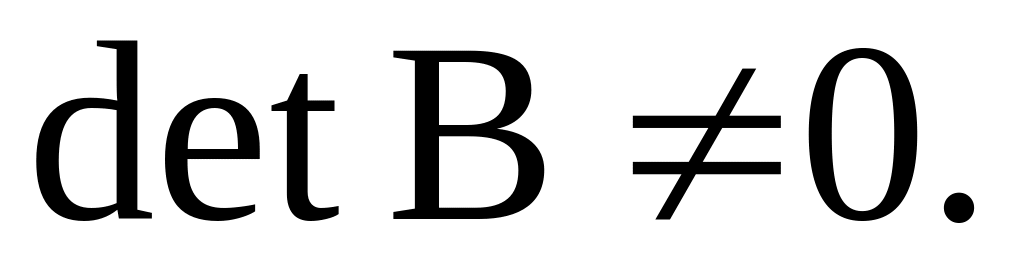
Элементарные преобразования матриц.

1. Отбрасывание нулевой строки (столбца).

2. Умножение всех элементов строки (столбца) на число, не равное нулю.

3. Изменение порядка строк (столбцов) матрицы.

4. Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5. Транспонирование матрицы.

Теорема. Ранг матрицы не изменяется при элементарных преобразованиях.

Определение. Матрицы А и B называются эквивалентными (АB), если матрица B получена из матрицы А в результате элементарных преобразований.

3.7 Нахождение ранга матрицы

Алгоритм Гаусса вычисления ранга матрицы.

1. Если все 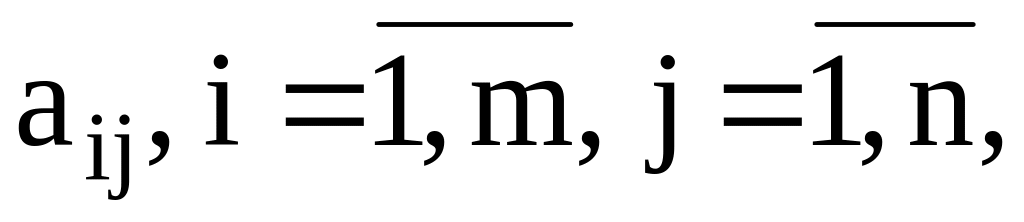то rangA = 0.

2. Выбираем элемент матрицы 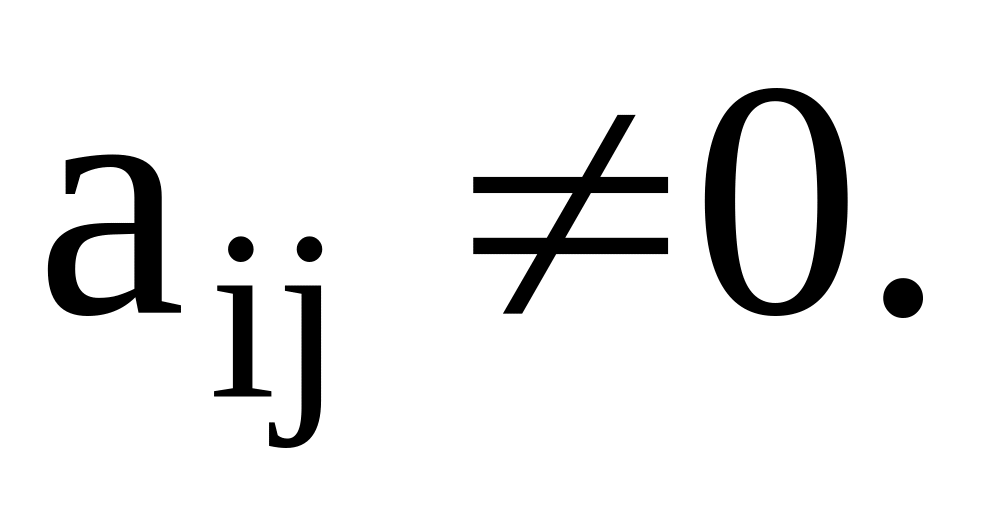Помещаем его в левый верхний угол матрицы и делим первую строку матрицы на С помощью элементарных преобразований обращаем все элементы первой строки в нули: 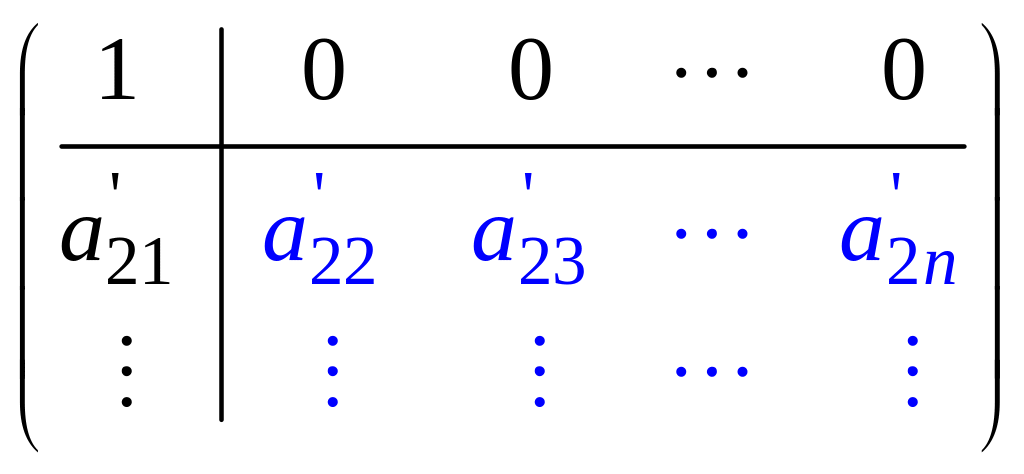. Если в части матрицы, выделенной синим цветом, все то rangA = 1.

3. Если хотя бы один элемент в области, выделенной синим цветом, отличен от нуля, алгоритм повторяем. Перестановкой строк и столбцов матрицы выбранный элемент помещаем на место второго элемента второй строки; делим всю вторую строку матрицы на этот элемент; элементы второй строки, начиная с третьего, обращаем в нули. Получим матрицу вида:

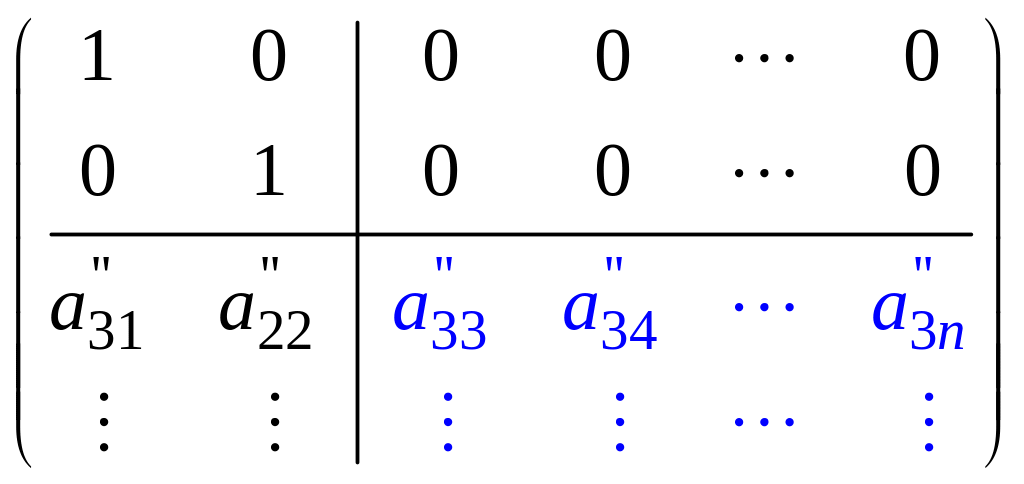. Если в части этой матрицы, выделенной синим цветом, то rang A = 2.

4. Если хотя бы один элемент 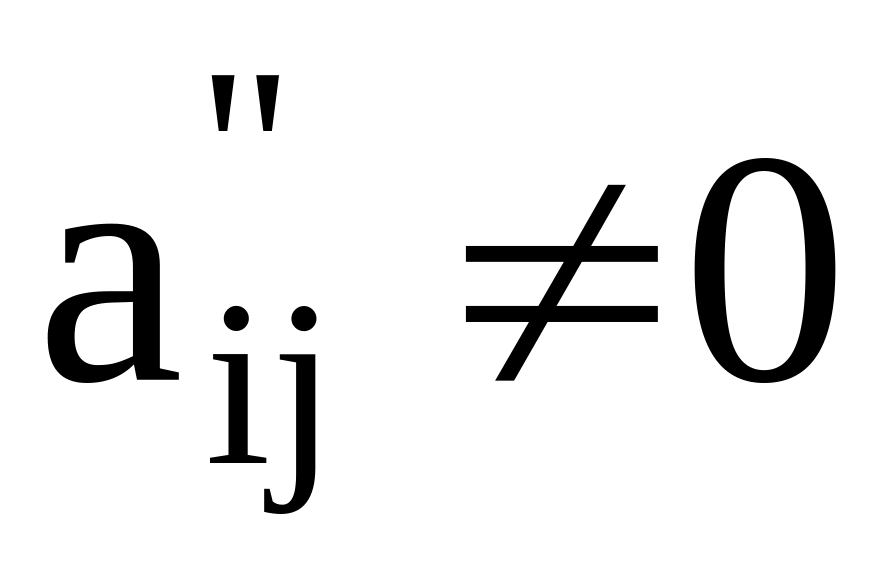в этой области, то алгоритм повторяем.

После r шагов получим матрицу ранга r вида:

Пример. Определить ранг и базисный минор матрицы:

Решение. Выполним следующие преобразования: первую, третью и четвертую строки поделим на 2, затем поменяем местами первый и второй столбцы:

 .

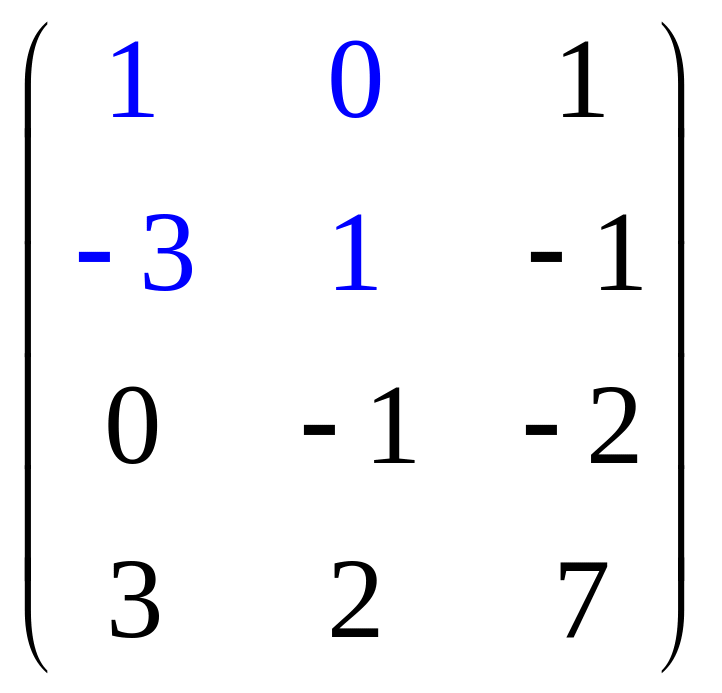Из третьего столбца вычтем первый, потом из него же вычтем второй, умноженный на два:



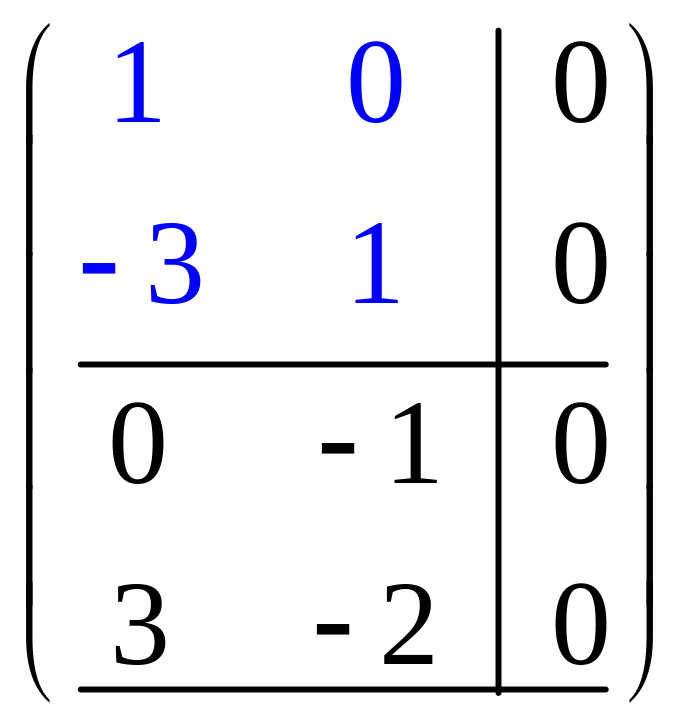
Очевидно, что ранг последней (а, значит, и исходной) матрицы равен 2.

Для того, чтобы определить базисный минор в исходной матрице, нам необходимо выделить базисные строки и столбцы. Для последней матрицы базисный минор выделен синим цветом. Проходя все действия в обратном порядке, определим базисный минор исходной матрицы.

Метод окаймляющих миноров.

Определение. Минор M₁ называется окаймляющим для минора М, если М получается из M₁ вычёркиванием одной крайней строки (первой или последней) и одного крайнего столбца.

Теорема. Если в матрице А размеров имеется минор порядка r, не равный нулю, а все его окаймляющие миноры порядка r+1 равны нулю, то rang A =r.

Пример. Для предыдущего примера:

Вычисляем минор второго порядка:

Выбираем миноры третьего порядка, в которые входят строки и столбы, дающие предыдущий минор. Таких миноров всего два:

Так как оба этих минора равны нулю, то ранг матрицы равен 2 (то есть порядку минора M₂).