5.3. Симплекс – метод решения злп
Симплекс (лат. simplex) –
простейший выпуклый многогранник в n-
мерном пространстве с n+1
вершиной (например, тетраэдр в трёхмерном
пространстве); симплексом является
также ОДР неравенства вида
Геометрический смысл симплекс-метода состоит в последовательном переходе от одной вершины многогранника ограничений (называемой первоначальной) к соседней, в которой линейная функция принимает лучшее (по крайней мере не худшее) значение (по отношению к цели задачи), до тех пор, пока не буде найдено оптимальное решение – вершина, где достигается оптимальное значение целевой функции (если задача имеет конечный оптимум).
Впервые симплекс-метод был предложен американским учёным Дж. Данцигом в 1949 г., однако, ещё в 1939 г. идеи метода были разработаны российским математиком Л.В.Канторовичем.
Для применения симплекс-метода общую ЗЛП следует записать в основной (канонической) форме:
(7) 
(8) 
(9)
Правила перехода к канонической форме.
Если требуется найти min F, то заменяя F на (-F), переходят к задаче максимизации, т.е. min F = max (-F).
Если ограничение является неравенством со знаком ≤, то от него переходят к равенству, прибавляя к левой части ограничения дополнительную неотрицательную переменную.
Если ограничение является неравенством со знаком ≥, то от него переходят к равенству, вычитая из левой части дополнительную неотрицательную переменную.
Если в задаче какая – либо из переменных произвольная, т.е. не подчиняется условию неотрицательности, то от неё избавляются, заменяя её разностью двух других неотрицательных переменных. Например, для произвольной переменной xk,
,
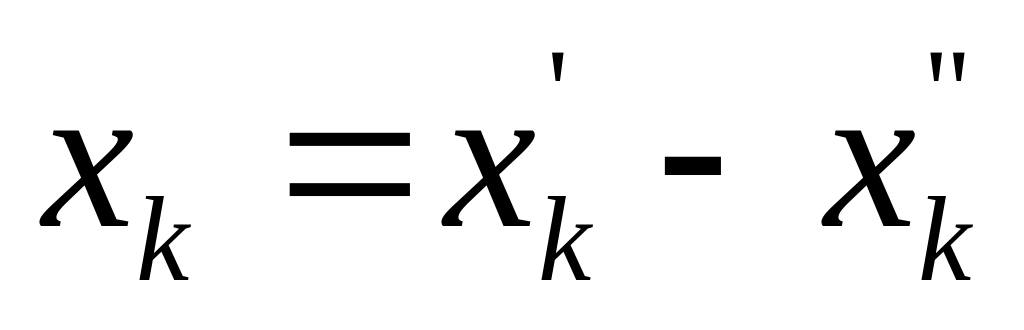где
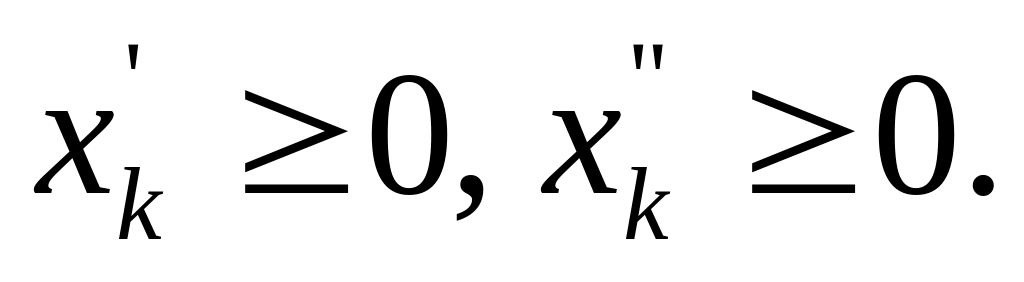
Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений – неравенств в ограничения–равенства равно числу преобразуемых неравенств.
Вводимые дополнительные переменные имеют вполне определённый смысл. Так, если в ограничениях исходной ЗЛП отражаются расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объёму неиспользованного соответствующего ресурса.
Задача (7) – (9) не всегда имеет решение. Во-первых, система уравнений (8) может оказаться несовместной. Во-вторых, она может оказаться совместной не в области неотрицательных решений. В-третьих, допустимые решения системы (8)-(9) существуют, но среди них нет оптимального: функция (F) неограничена в ОДР. Предположим, что все уравнения системы (8) линейно независимы, т.е. выражают независимые друг от друга условия задачи.
Если это не так, то лишние уравнения нужно исключить. Задачу (7)-(9) имеет смысл решать, когда число уравнений в системе (8) ограничений меньше числа входящих в них неизвестных: m<n. Иначе, если m=n, то система (8) имеет единственное решение и задача максимизации функции (7) не имеет смысла; если m>n, то система (8) переопределена и в общем случае не имеет решений.
Если m<n, то система (8) имеет бесконечное множество решений и среди них можно выбрать оптимальное, в котором целевая функция достигает своего максимума.
Симплекс–метод является методом направленного перебора решений системы (8)-(9). Каждое следующее решение улучшает значение целевой функции.
Симплекс – метод включает 2 этапа:
определение начального решения, удовлетворяющего ограничениям (8)-(9);
последовательное улучшение начального решения и получение оптимального решения задачи(8) - (9) .
Система (8) содержит m линейно независимых уравнений и их число меньше числа неизвестных, входящих в систему, следовательно, систему (8) можно разрешить относительно m неизвестных, например, x1, x2,…, xm, выразив их через остальные неизвестные:
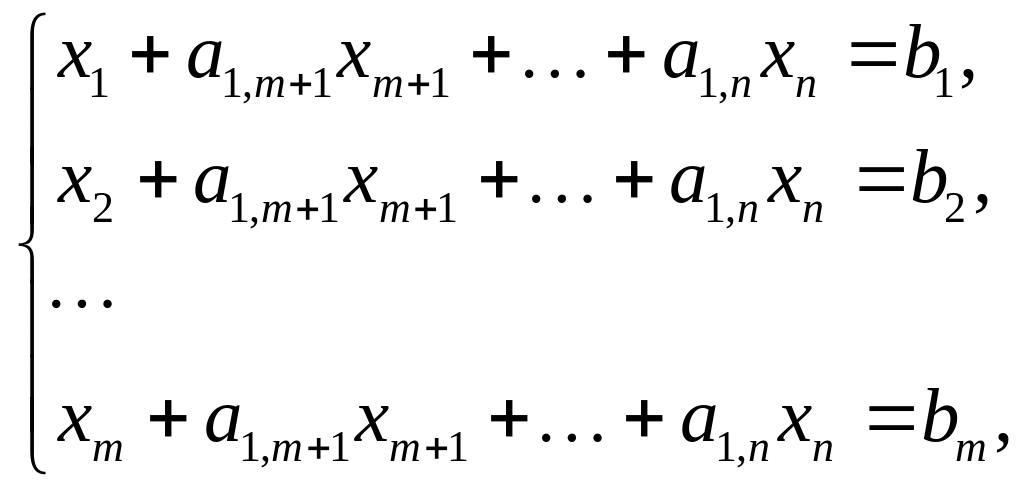(10)
Форма ЗЛП (7), (9), (10) называется стандартной.
Векторная форма этой задачи имеет вид:
(11)
,
(12)
(13)
где система
имеет вид:
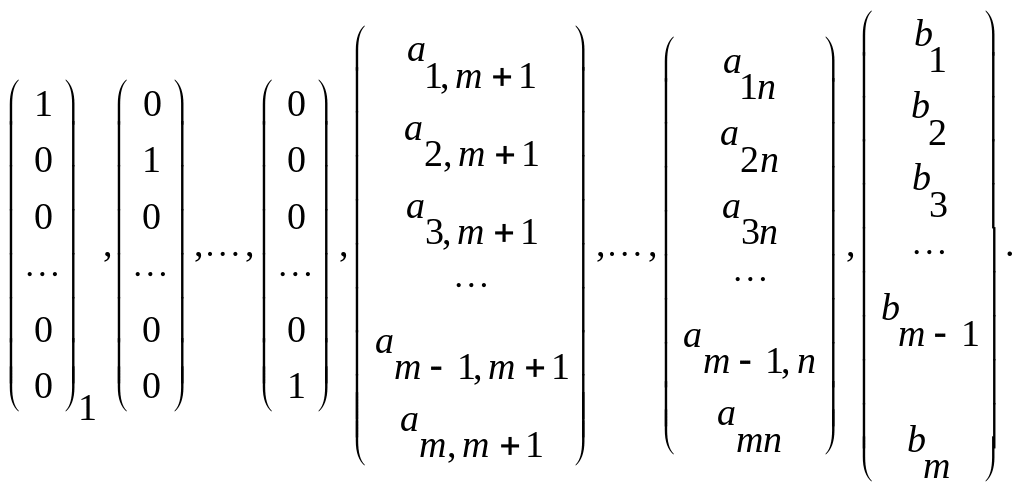
Определение. План X=(x1, x2, …, xn) называется опорным планом ЗЛП, если положительные коэффициенты (xj>0) состоят при линейно независимых векторах Рj. Опорный план называется невырожденным, если он содержит ровно m положительных компонент, иначе - вырожденным.
Из данного определения следует, что
план X=(b1,
b2, …, bm,
0, 0, …, 0) является опорным планом. Он
определяется системой единичных векторов
Р1, Р2, …, Рm,
которые образуют единичный базис
пространства Rm,
следовательно, каждый из векторов Рj,
можно
разложить по этому базису:
Положим
Теорема 1 (признак оптимальности
опорного плана). Опорный план
задачи
(11)-(13) является оптимальным планом, если
∆j≥0,
.
Теорема 2. Если j<0
для некоторого j=k
и среди чисел aik,
,
нет положительных (aik0,
),
то целевая функция (11) задачи (11)-(13) не
ограничена на множестве её планов.
Теорема 3. Если опорный план
задачи (5) - (7) не вырожден и ∆k
< 0, но среди чисел aik,
,
еcть m
положительных (не все aik≤0,
),
то существует опорный план
,
такой, что F(
)>F(X).
Таблица1.
Устройство симплекс-таблицы.
i |
базис |
|
|
с1 |
с2 |
… |
сr |
… |
сm |
сm+1 |
… |
сk |
… |
сn |
|
|
сб |
Р0 |
P1 |
P2 |
…. |
Pr |
… |
Pm |
Pm+1 |
… |
Pk |
… |
Pn |
1 |
P1 |
с1 |
b1 |
1 |
0 |
… |
0 |
… |
0 |
a1,m+1 |
… |
a1k |
… |
a1n |
2 |
P2 |
с2 |
b2 |
0 |
1 |
… |
0 |
… |
0 |
a2,m+1 |
… |
a2k |
… |
a2n |
… |
… |
… |
… |
… |
… |
…. |
… |
… |
… |
…. |
… |
… |
… |
… |
R |
Pr |
сr |
br |
0 |
0 |
… |
1 |
… |
0 |
a r,m+1 |
… |
ark |
… |
arn |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
…. |
… |
… |
… |
… |
m |
Pm |
сm |
bm |
0 |
0 |
… |
0 |
… |
1 |
am,m+1 |
… |
amk |
… |
arm |
m+1 |
|
|
F0 |
0 |
0 |
… |
0 |
… |
0 |
m+1 |
… |
∆k |
… |
∆n |
Таблица 2.
i |
базис |
|
|
c1 |
c2 |
… |
cr |
… |
cm |
cm+1 |
… |
ck |
… |
cn |
|
|
cб |
Р0 |
P1 |
P2 |
… |
Pr |
… |
Pm |
Pm+1 |
… |
Pk |
… |
Pn |
1 |
P1 |
c1 |
|
1 |
0 |
… |
|
… |
0 |
|
… |
0 |
… |
|
2 |
P2 |
c2 |
|
0 |
1 |
… |
|
… |
0 |
|
… |
0 |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
r |
Pr |
cr |
|
0 |
0 |
… |
|
… |
0 |
|
… |
1 |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
m |
Pm |
cm |
|
0 |
0 |
… |
|
… |
1 |
|
… |
0 |
… |
|
m+1 |
|
|
|
0 |
0 |
… |
|
… |
0 |
|
… |
0 |
… |
|
В столбце cб записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.
В столбце Р0 записывают положительные компоненты исходного опорного плана, в нём же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов Рj представляют собой столбцы коэффициентов разложения этих векторов по векторам данного базиса.
Первые m строк симплекс-таблицы определяются исходными данными, а показатели (m+1)-ой строки вычисляют. В этой строке в столбце вектора P0 записывается значение F0 целевой функции, которое она принимает при данном опорном плане, а в столбце вектора Рj - значения
∆j = zj-cj,
zj=(cj,pj)=
;
F0 =(cб,P0)=
.
После заполнения симплекс-таблицы исходный опорный план проверяют на оптимальность. Для этого просматривают элементы (m+1)-ой строки таблицы.
В результате может иметь место один из следующих случаев:
∆j≥0,
,
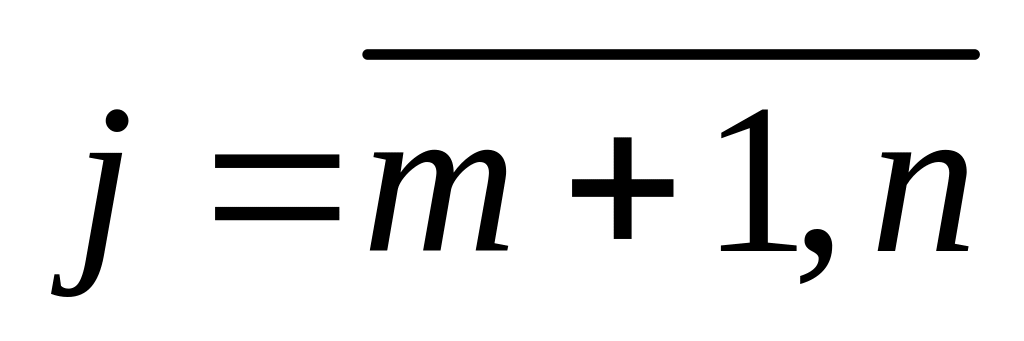исходный опорный план оптимальный;
∆j≤0 для некоторого ј и все соответствующие этому индексу величины aij≤0, ,- целевая функция не ограничена сверху на множестве планов;
∆j<0 для некоторых индексов j и для каждого такого j по крайней мере одно из чисел aij>0. В этом случае можно перейти от исходного к новому опорному плану, при котором значение целевой функции увеличится. Этот переход осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора.
В качестве вектора, вводимого в базис, выбирают вектор, соответствующий максимальному по модулю отрицательному числу ∆ј. Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел cj, определяемых данными числами ∆ј (∆ј <0).
Для определения вектора, подлежащего исключению из базиса, находят min (bi/aik)=Ө0 для всех aik >0. Пусть этот минимум достигается при i=r. Тогда из базиса исключается вектор Pr, а число ark называется разрешающим элементом. Столбец и строка, на пересечении которых находится разрешающий элемент, называются разрешающими.
После выделения разрешающих строки и столбцов находят новый опорный план и коэффициенты разложения векторов Pj через векторы нового базиса, соответствующего новому опорному плану. Переход к нему сводится к переходу от одной симплекс-таблицы к другой.
Правила перехода к новой симплекс-таблице.
В столбцах векторов, входящих в базис, на пересечении строк и столбцов векторов с одинаковыми номерами проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю.
Элементы векторов Р0 и Рj в строке новой симплекс-таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце cб вводимого вектора проставляют величину
,
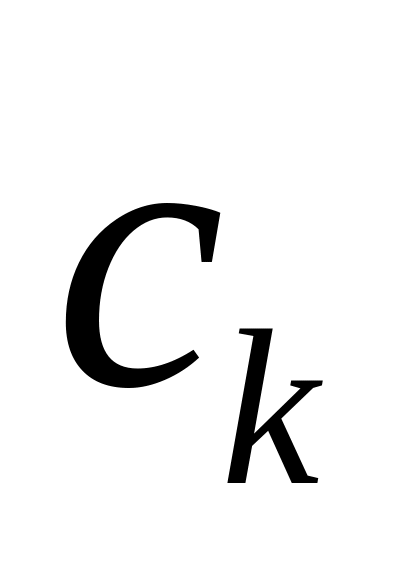где k - индекс вводимого вектора.Остальные элементы столбцов Р0 и Рj новой симплекс-таблицы вычисляются по правилу треугольника. Для вычисления какого-нибудь из этих элементов находят 3 числа:
число, стоящее в исходной симплекс-таблице на месте искомого элемента новой симплекс-таблицы;
число, стоящее в исходной симплекс-таблице на пересечении строки, в которой находится искомый элемент новой симплекс-таблицы и столбца, соответствующего вектору, вводимому в базис;
число, стоящее в новой симплекс-таблице на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимого в базис вектора.
Эти 3 числа образуют треугольник, 2 вершины которого соответствуют числам, находящимся в исходной симплекс-таблице, а третья – числу, находящемуся в новой симплекс-таблице. Для определения искомого элемента новой симплекс-таблицы из первого числа вычитают произведение второго и третьего.
После заполнения новой симплекс-таблицы просматривают элементы (m+1)-ой строки. Если все ∆ј≥0, ,то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную выше последовательность действий, находят новый опорный план. Этот процесс продолжается до тех пор, пока либо получают оптимальный план задачи, либо устанавливают её неразрешимость.
Пример. Для изготовления различных изделий А, В и С предприятие использует 3 различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, представлены в таблице.
Вид сырья |
Нормы затрат сырья На одно изделие(кг.) |
Общее кол-во сырья |
||
|
А |
В |
С |
|
1 |
18 |
15 |
12 |
360 |
2 |
6 |
4 |
8 |
192 |
3 |
5 |
3 |
3 |
180 |
Цена одного изд. |
9 |
10 |
16 |
|
Изделия А, В, С могут производиться в любых соотношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьём каждого вида.
Необходимо составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.
Решение. Искомый выпуск изделий А обозначим через х1, изделий В – через х2, изделий С- через х3.
Общая ЗЛП:
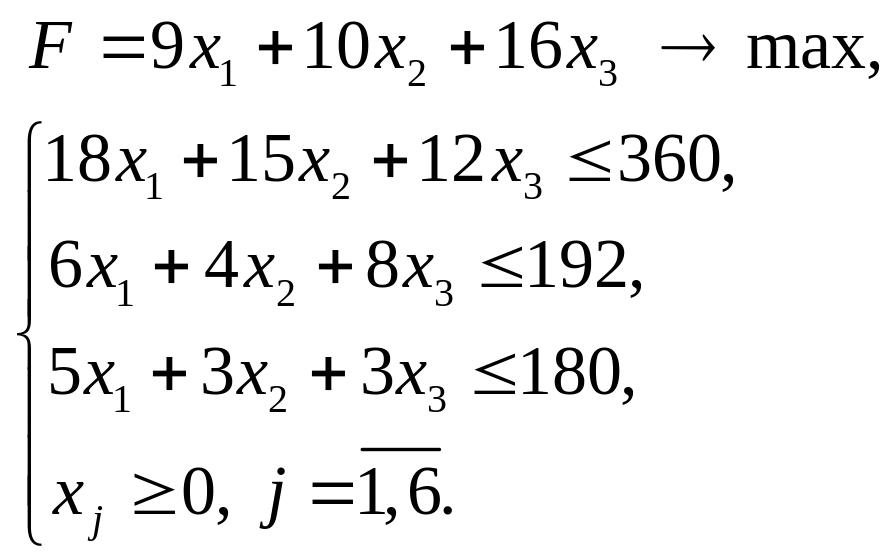
Канонический вид:
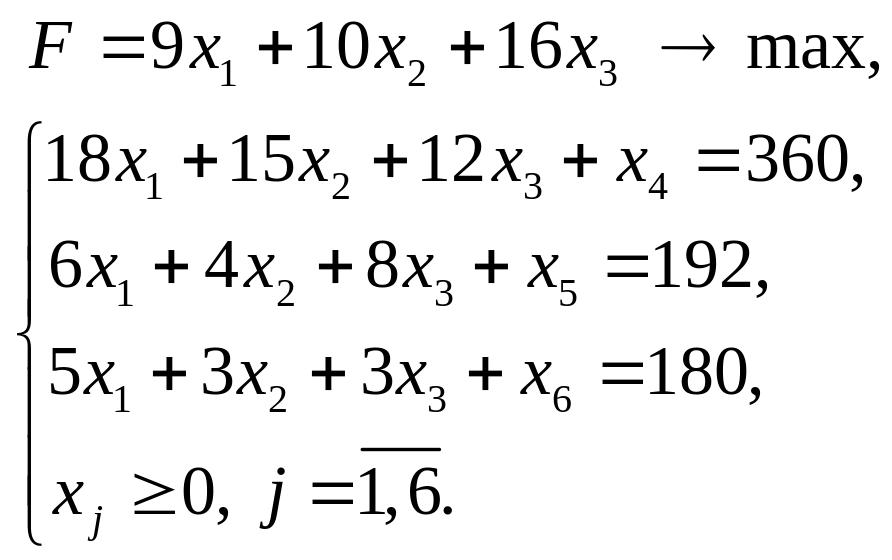
Запишем полученную систему в векторной форме:
x1Р1+x2Р2+x3Р3+x4Р4+x5Р5+x6Р6=Р0,
где
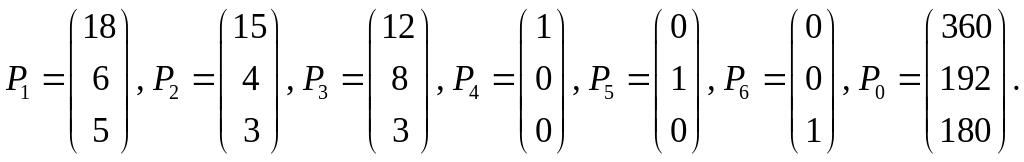Т.к.
среди векторов Рj,
,
имеются 3 единичных вектора Р4,
Р5, Р6, то переменные х4,
х5, х6 будут базисными,
остальные переменные х1, х 2,х3
– свободными. Свободные переменные
полагаем равными 0. Тогда из канонического
вида ЗЛП следует, что х4=360, х5=192,
х6=180. Таким образом, для данной
ЗЛП можно непосредственно записать
опорный план Х=(0, 0, 0, 360, 192, 180), определяемый
системой трёхмерных единичных векторов
Р4, Р5, Р6, которые
образуют единичный базис пространства
R3. Начальное значение
F0 целевой функции
при этом будет равно 0.
Все вычисления оформляем в виде последовательности симплекс-таблиц.
i |
Базис |
cб |
Р0 |
9 |
10 |
16 |
0 |
0 |
0 |
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
||||
1 |
Р4 |
0 |
360 |
18 |
15 |
12 |
1 |
0 |
0 |
2 |
Р5 |
0 |
192 |
6 |
4 |
8 |
0 |
1 |
0 |
3 |
Р6 |
0 |
180 |
5 |
3 |
3 |
0 |
0 |
1 |
4 |
|
|
0 |
-9 |
-10 |
-16 |
0 |
0 |
0 |
1 |
Р4 |
0 |
72 |
9 |
9 |
0 |
1 |
-3/2 |
0 |
2 |
Р3 |
16 |
24 |
¾ |
½ |
1 |
0 |
1/8 |
0 |
3 |
Р6 |
0 |
108 |
11/4 |
3/2 |
0 |
0 |
-3/8 |
1 |
4 |
|
|
384 |
3 |
-2 |
0 |
0 |
2 |
0 |
1 |
Р2 |
10 |
8 |
1 |
1 |
0 |
1/9 |
-1/6 |
0 |
2 |
Р3 |
16 |
20 |
¼ |
0 |
1 |
-1/18 |
5/24 |
0 |
3 |
Р6 |
0 |
96 |
5/4 |
0 |
0 |
-1/6 |
-1/8 |
1 |
4 |
|
|
400 |
5 |
0 |
0 |
2/9 |
5/3 |
0 |
Для первой симплекс-таблицы вычисляем
величины ∆j=(cб,Pj)-cj,
Для векторов базиса ∆j=0,
,
∆1=(cб,P1)-с1=-9,
∆2=(сб,P2)-с2=-10,
∆3=(сб,P3)-с3=-16.
Т.к. среди чисел ∆j, , имеются отрицательные числа, то данный опорный план не является оптимальным. Находим максимальное по модулю отрицательное значение ∆j=-16. Столбец, в котором оно находится, определяет вектор, выводимый из базиса, т.е. вектор Р3. Столбец вектора Р3 будет разрешающим столбцом.
Для определения вектора, выводимого из базиса, определяем значение
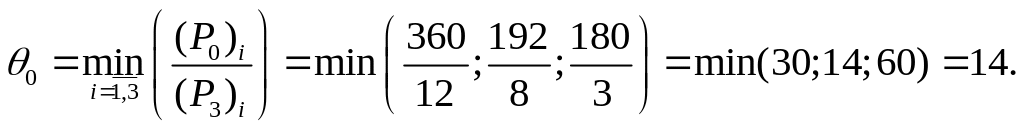
Знаменатель дроби 192/8, т.е. число 8, будет разрешающим элементом. Строка, в которой он находится, указывает на вектор, выводимый из базиса, т.е. вектор Р5.
Составляем симплекс-таблицу первой итерации. Сначала заполняем строку, номер которой совпадает с номером строки предыдущей симплекс-таблицы, в которой находится вектор Р5, т.е. вторую строку. Ее элементы получаются из соответствующих элементов второй строки предыдущей симплекс-таблицы делением на разрешающий элемент, т.е. на 8. При этом в столбце cб записываем коэффициент с3=16, стоящий в столбце вводимого в базис вектора Р3. Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов векторов с одинаковыми номерами проставляем 1, на пересечении строк и столбцов с разными номерами проставляем 0. ∆j для векторов базиса так же равны 0.
Для определения остальных элементов второй симплекс-таблицы применяем правило треугольника. Вычислим, например, первое число в столбце вектора Р0. Для этого находим 3 числа:
число, стоящее в предыдущей симплекс-таблице на пересечении столбца вектора Р0 и первой строки, т.е. 360;
число, стоящее в предыдущей симплекс-таблице на пересечении столбца вектора Р3 (разрешающего столбца) и первой строки, т.е. 12;
число, стоящее в новой симплекс-таблице на пересечении столбца вектора Р0 и второй строки (разрешающей строки), т.е. 24.
Вычитая из первого числа произведение
двух других, находим искомый элемент:
,
записываем его в первой строке столбца
вектора Р0.
Для вычисления 3-го числа столбца вектора Р0 используется 3-я строка предыдущей симплекс-таблицы.
Аналогично вычисляются остальные элементы симплекс-таблицы второй итерации. Для вычисления элементов ее 4-й строки используется 4-я строка предыдущей симплекс-таблицы.
Среди чисел ∆j,
новой симплекс-таблицы есть одно
отрицательное число
.
Поэтому найденный опорный план не
является оптимальным и в базис надо
ввести вектор Р2. Для определения
вектора, выводимого из базиса, вычисляем
значение
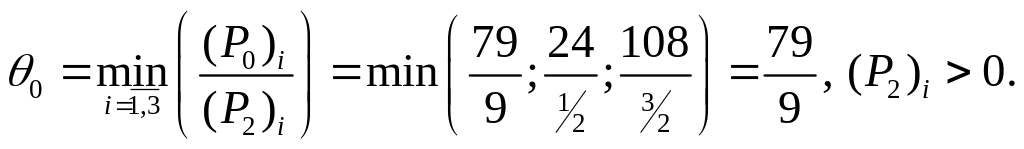
Число 9, стоящее в первой строке второй симплекс-таблицы, определяет вектор, подлежащий выводу из базиса, т.е. вектор Р2. Составляем симплекс-таблицу второй итерации. Её элементы вычисляем аналогично элементам предыдущей симплекс-таблицы, используя их для определения значений новой симплекс-таблицы. В четвёртой строке третьей симплекс-таблицы все ∆j≥0, . Следовательно, полученный на последней итерации опорный план Х=(0;8; 20; 0; 0; 96) является оптимальным и Fmax=400. Нужно изготовить 8 изделий В и 20 изделий С. При данном плане выпуска изделий полностью используется сырье 1 и 2 вида, а стоимость производимой продукции равна 400 д.е.