
- •Введение
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов
- •1. Элементы теории множеств и комплексных чисел
- •1.1. Понятие множества. Операции над множествами
- •1.2. Числовые множества и их свойства.
- •2. Алгебра многочленов.
- •Глава 2. Матрицы. Определители
- •1. Алгебра матриц.
- •Виды матриц.
- •2. Определитель n-го порядка.
- •2.1. Определение. Вычисление определителей 2 и 3-го порядков.
- •2.2.Миноры и алгебраические дополнения.
- •2.3.Свойства определителя n-го порядка.
- •3. Действия над матрицами.
- •3.1.Линейные операции над матрицами.
- •3.2. Умножение матриц.
- •3.3. Многочлены от матриц.
- •3.4. Обратная матрица.
- •Вычисление обратной матрицы (через алгебраические дополнения).
- •3.5. Линейная зависимость строк и столбцов матрицы.
- •3.6. Ранг матрицы. Базисный минор.
- •3.7 Нахождение ранга матрицы
- •Вопросы для повторения.
- •Глава 3. Системы линейных уравнений и методы их решения.
- •1. Основные понятия и определения
- •2. Условия совместности системы линейных уравнений
- •3. Метод обратной матрицы
- •4. Правило Крамера
- •5. Метод Гаусса исключения неизвестных
- •7. Метод полного исключения
- •7.1. Решение систем линейных уравнений
- •7.2. Вычисление обратной матрицы методом полного исключения.
- •7.3. Вычисление ранга матрицы методом полного исключения
- •8. Собственные значения и собственные векторы матриц
- •9. Квадратичные формы
- •10. Численные методы решения систем линейных уравнений
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 4. Векторная алгебра
- •Векторное произведение двух векторов.
- •Вопросы для повторения.
- •Глава 5. Задачи линейного программирования
- •5.1. Постановка задачи линейного программирования (злп)
- •5.2. Графический метод решения злп
- •5.3. Симплекс – метод решения злп
- •Глава 6. Балансовые модели
- •6.1. Экономико-математическая модель (эмм) межотраслевого стоимостного баланса (модель Леонтьева)
- •Модель международной торговли
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Библиографический список
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов 4
- •Глава 2. Матрицы. Определители 17
- •Глава 3. Системы линейных уравнений и методы их решения. 51
- •Глава 4. Векторная алгебра 95
- •Глава 5. Задачи линейного программирования 110
- •Глава 6. Балансовые модели 128
Глава 6. Балансовые модели
Под балансовой моделью понимается система уравнений, которые удовлетворяют требованиям соответствия наличия ресурса и его использования.
6.1. Экономико-математическая модель (эмм) межотраслевого стоимостного баланса (модель Леонтьева)
Предполагается, что для производства единицы продукции в j-ой отрасли требуется определённое количество затрат промежуточной продукции i-ой отрасли, равное aij. Величины aij называются коэффициентами прямых материальных затрат и рассчитываются следующим образом:
![]() (1)
(1)
где xij – величины межотраслевых потоков продукции, i и j – номера соответственно отраслей производящих и потребляющих, Xj – валовой продукт j-ой отрасли. Коэффициент прямых материальных затрат показывает, какое количество продукции i-ой отрасли необходимо, если учитывать только прямые затраты для производства единицы продукции j-ой отрасли.
Валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих её продукцию отраслей и конечной продукции данной отрасли:
![]() (2)
(2)
С учётом (1) систему уравнений баланса (2) можно переписать в виде
![]() (3)
(3)
Если ввести в рассмотрение матрицу
коэффициентов прямых материальных
затрат
![]() вектора-столбцы валовой продукции X и
конечной продукции Y:
вектора-столбцы валовой продукции X и
конечной продукции Y:
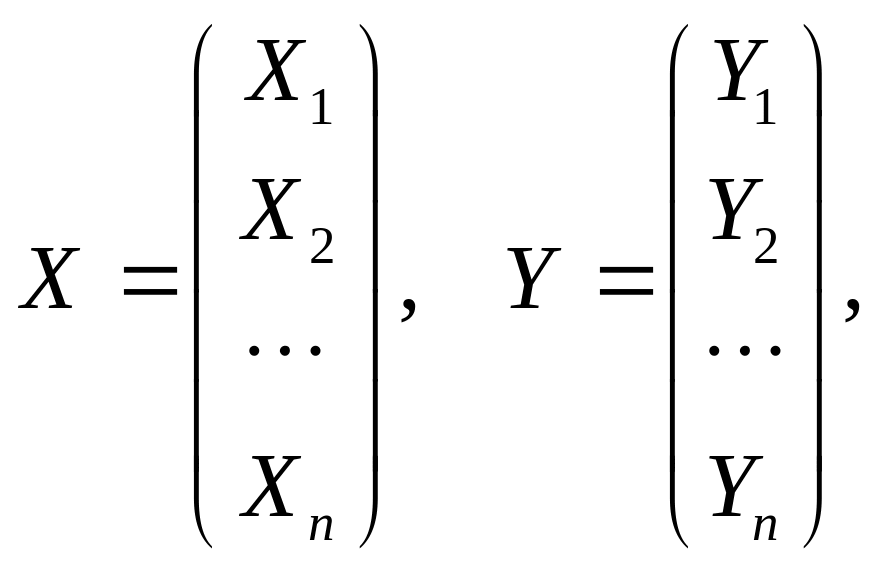
то система уравнений (3) в матричной форме примет вид
X=AX+Y. (4)
Cистема уравнений (3), или в матричной форме (4), называется ЭММ межотраслевого баланса (моделью Леонтьева или моделью «затраты-выпуск»). С её помощью можно выполнять три варианта расчётов:
задав в модели величины Xi валовой продукции каждой отрасли, можно определить объёмы конечной продукции каждой отрасли: Y=(I-A)X, (5) где I – единичная матрица порядка n;
задав величины Yi, можно определить величины Xi валовой продукции каждой отрасли: X=BY, (6) где B=(I-A)-1 – обратная матрица к матрице I-A;
для ряда отраслей задав величины валовой продукции, а для всех остальных отраслей задав объёмы конечной продукции, можно найти величины конечной продукции первых отраслей и объёмы валовой продукции вторых, в этом варианте расчёта удобней пользоваться системой линейных уравнений (3).
Элементы матрицы B будем обозначать через bij, тогда из матричного уравнения (6) для любой i-ой отрасли можно получить соотношение:
![]() (7)
(7)
Коэффициенты bij называются коэффициентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков. Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в производство продукта не прямо, а через другие (промежуточные) средства производства.
Коэффициент bij полных материальных затрат можно применять, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объёмов конечной продукции всех отраслей:
![]() (8)
(8)
где Xi и Yj – изменения (приросты) величин валовой и конечной продукции соответственно.
Основные свойства матрицы А коэффициентов прямых материальных затрат.
А0, т.е.
 для
всех
для
всех
 ,
,
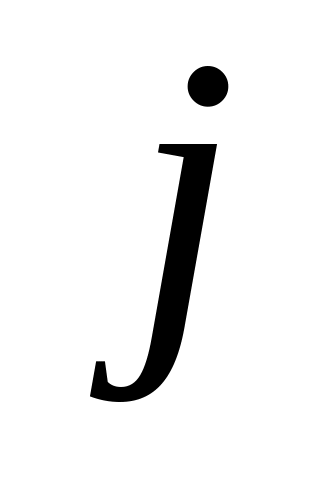 от
от
 до
до
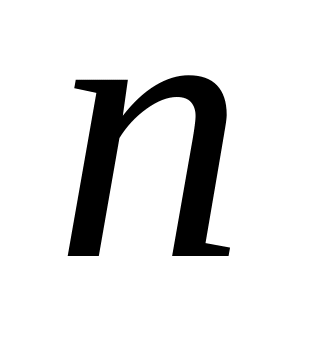 .
. для всех
от
до
.
для всех
от
до
.
Заметим, что вектор Х валовой продукции состоит из неотрицательных компонент.
Определение. Неотрицательная матрица А называется продуктивной, если существует такой неотрицательный вектор X0, что
X>АX. (9)
Очевидно, что условие (9) означает существование положительного вектора конечной продукции Y>0 для модели межотраслевого баланса (4).
Теорема. Для того, чтобы матрица А коэффициентов прямых материальных затрат была продуктивной, необходимо и достаточно, чтобы выполнялось одно из следующих условий:
матрица I-A неотрицательно обратима, т.е. существует обратная матрица (I-A)-10;
матричный ряд I+A+A2+A3+=
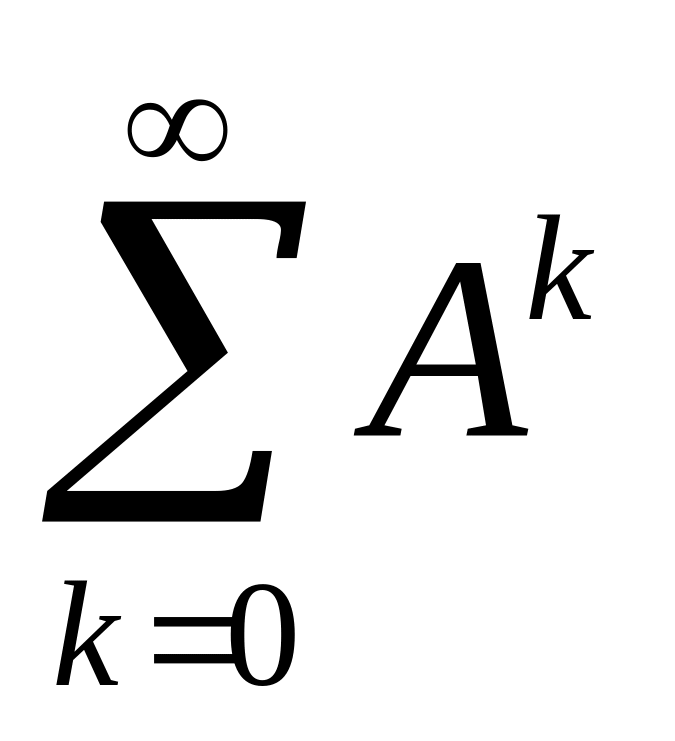 cходится,
причём его сумма равна обратной матрице
(I-A)-1;
cходится,
причём его сумма равна обратной матрице
(I-A)-1;наибольшее по модулю собственное значение λ матрицы А, т.е. решение характеристического уравнения det(А- λI)=0, строго больше 1;
все главные миноры матрицы I-A, т.е. определители матриц, образованных элементами первых строк и первых столбцов этой матрицы, порядков от 1 до n, положительны.
Существует другое определение коэффициента полных материальных затрат.
Определение. Коэффициентом cij полных материальных затрат называется сумма прямых и косвенных затрат продукции i-ой отрасли для производства продукции j-ой отрасли через все промежуточные продукты на всех предшествующих стадиях производства.
Между двумя матрицами B и C коэффициентов полных материальных затрат существует следующая связь:
B=I+C,
или в поэлементной записи
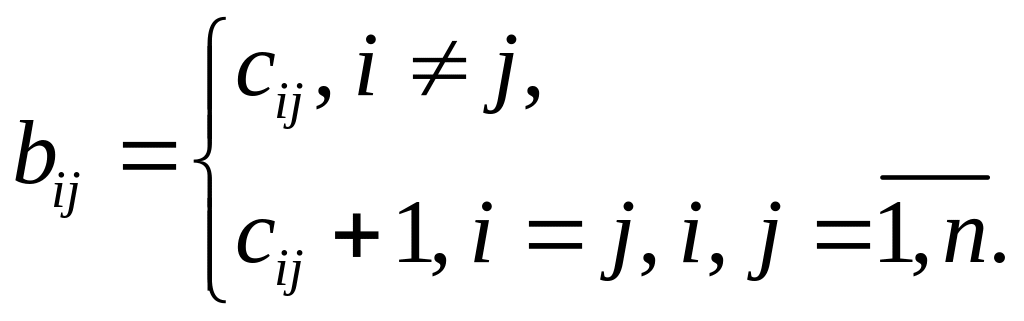
Данная связь определяет экономический смысл различия между коэффициентами матриц B и C: в отличие от коэффициентов матрицы C, учитывающих только затраты на производство продукции, коэффициенты матрицы B включают в себя кроме затрат также саму единицу конечной продукции, которая выходит за сферу производства.
Матрица А коэффициентов прямых материальных затрат задаётся и является продуктивной. Матрицу B можно найти одним из следующих способов.
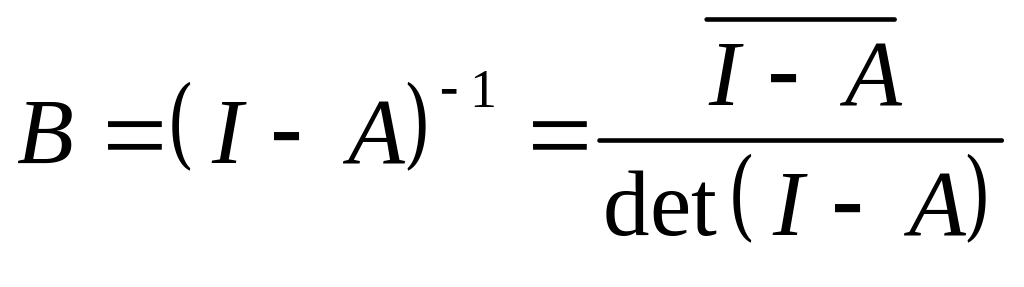 ,
где
,
где
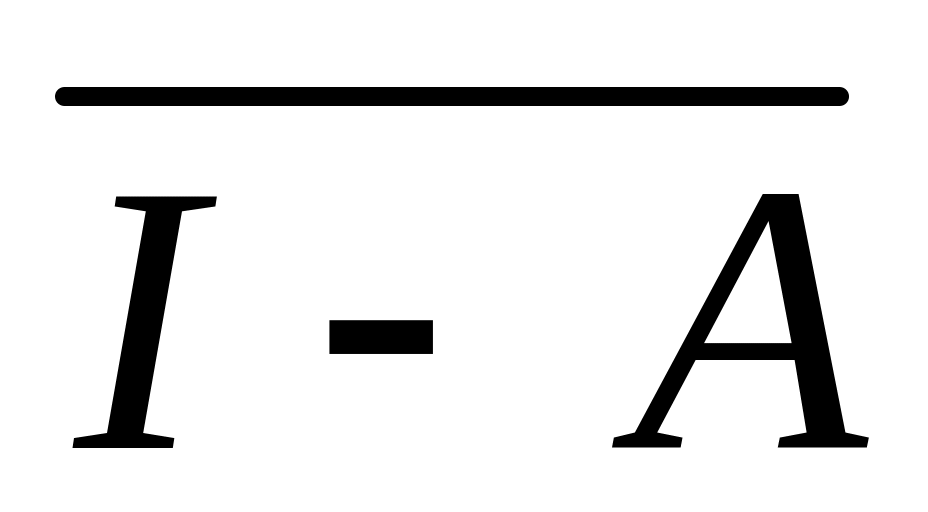 - матрица, присоединённая к матрице
I-A, det(I-A) – определитель матрицы I-A.
Элементами матрицы
являются алгебраические дополнения
элементов матрицы (I-A)T,
транспонированной к матрице I-A.
- матрица, присоединённая к матрице
I-A, det(I-A) – определитель матрицы I-A.
Элементами матрицы
являются алгебраические дополнения
элементов матрицы (I-A)T,
транспонированной к матрице I-A.Метод Жордана-Гаусса. Справа к матрице I-A приписывается матрица I. В результате гауссовых преобразований слева получается матрица I, а справа – матрица
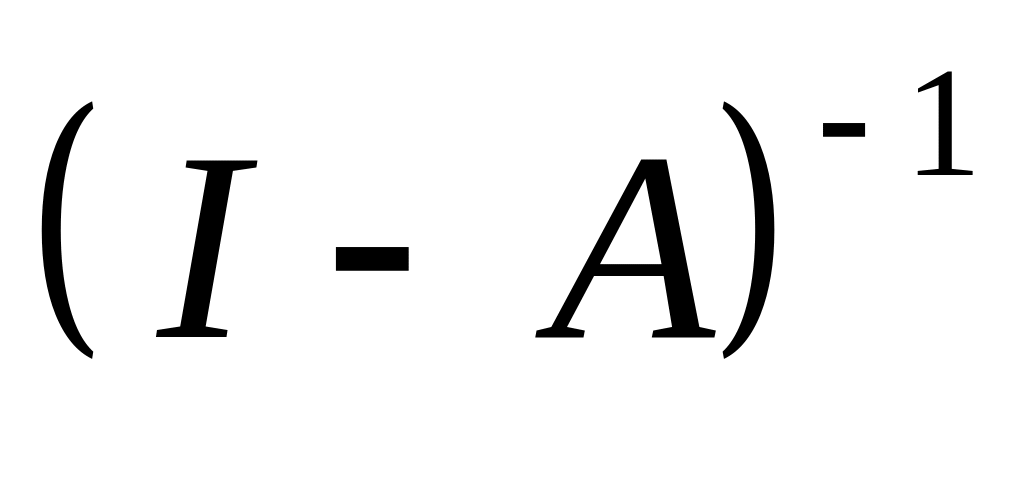 .
.Приближённое вычисление матрицы В, используя разложение в матричный ряд
![]()
Обязательным условием корректности этих расчётов является продуктивность матрицы I-A. При расчётах ограничиваются учётом косвенных материальных затрат до некоторого порядка включительно, например, до второго и третьего порядков. В этом способе коэффициенты полных материальных затрат получаются с приближением по недостатку.
Пример. Задана матрица А коэффициентов затрат трёх отраслей и вектор конечной продукции Y.
Проверить продуктивность матрицы I-A.
Построить баланс производства и распределения продукции отраслей.
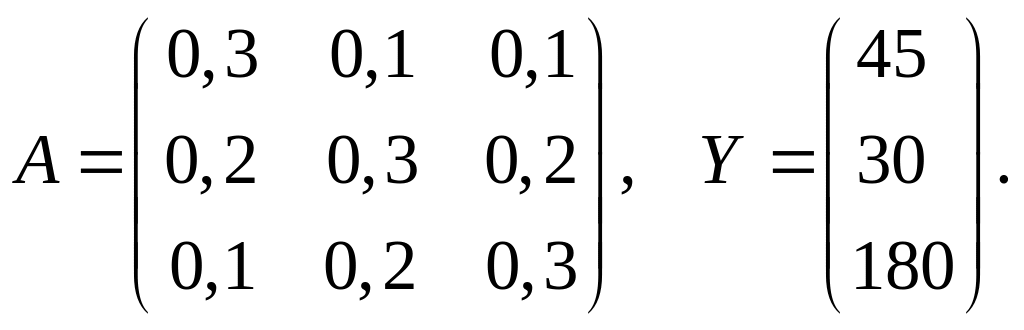
Решение. Проверим выполнение первого
условия продуктивности матрицы I-A.
матрица А должна быть неотрицательно
обратима, т.е. должна существовать
обратная матрица (I-A)-10.
Чтобы проверить это, используем второе
свойство: матричный ряд
![]() должен сходиться и его сумма равна
.
Найдём вектор-столбец X
валовой продукции по отраслям.
должен сходиться и его сумма равна
.
Найдём вектор-столбец X
валовой продукции по отраслям.
X=BY, где B=(I-A)-1.
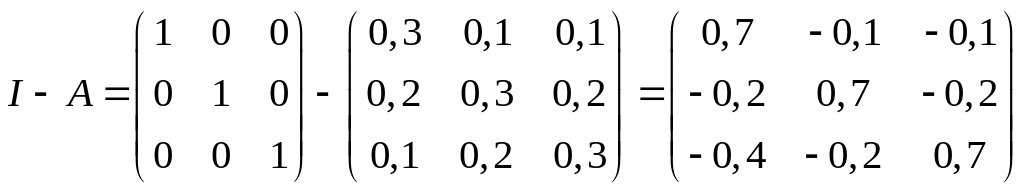
![]()
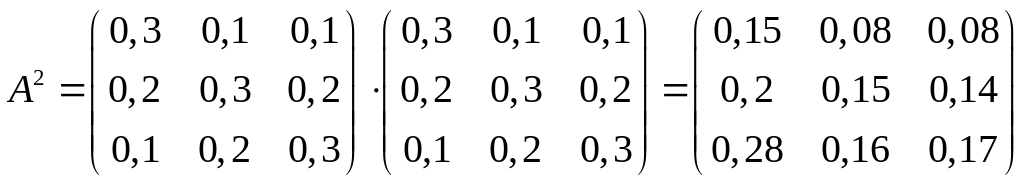
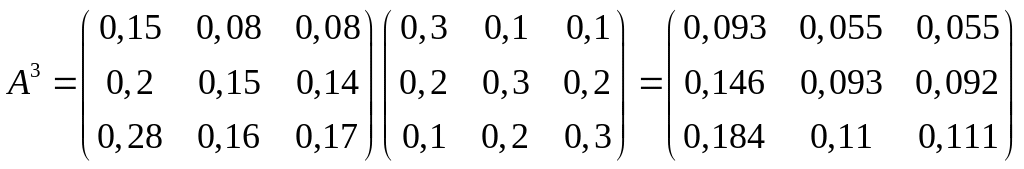
![]()
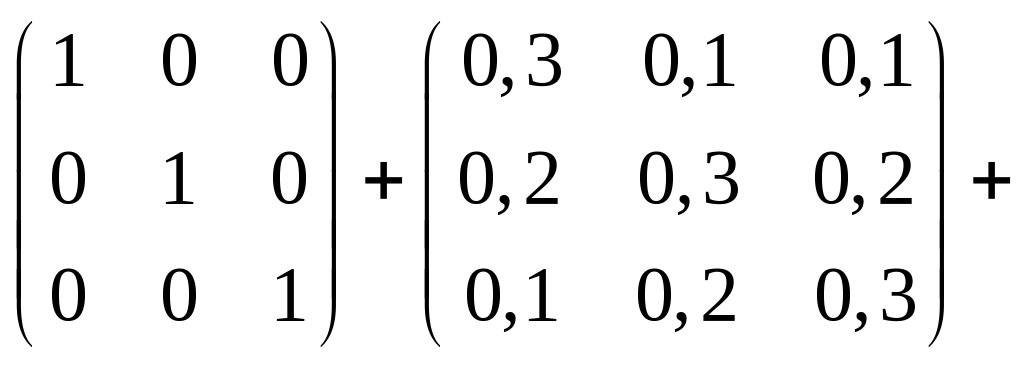
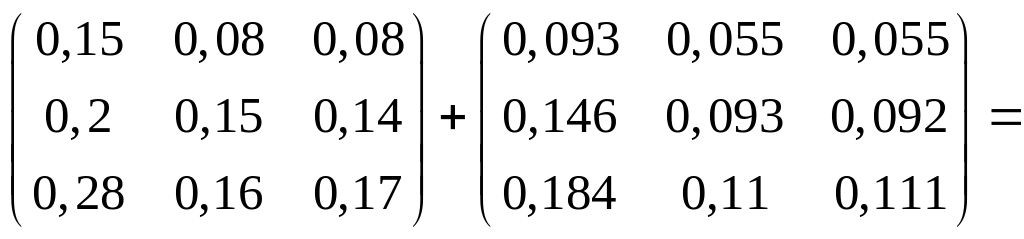

Матрица В не содержит отрицательных элементов матрица А продуктивна она позволяет обеспечить определённый выпуск конечной продукции по всем отраслям.
Найдём вектор-столбец X=BY валовой продукции по отраслям.
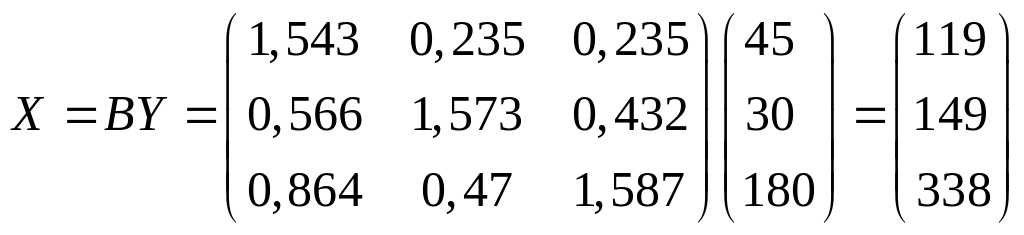
Для нахождения первого столбца матрицы межотраслевого баланса нужно элементы первого столбца заданной матрицы А умножить на элемент x1 вектора-столбца Х.
0,3119=35,7
0,2119=23,8
0,4119=47,6 Аналогично вычисляются элементы второго и третьего столбцов матрицы межотраслевого баланса.
0,1149=14,9 0,1338=33,8
0,3149=44,7 0,2338=67,6
0,2149=29,8 0,3338=101,4
Отрасли производящие |
Отрасли потребляющие |
Конечная продукция Y |
Валовая продукция X |
||
1 |
2 |
3 |
|||
1 |
35,7 |
14,9 |
33,8 |
45 |
119 |
2 |
23,8 |
44,7 |
67,6 |
30 |
149 |
3 |
47,6 |
29,8 |
101,4 |
180 |
338 |
Условно чистая продукция |
11,9 |
59,6 |
135,2 |
255 |
|
Валовая продукция |
119 |
149 |
338 |
|
606 |
Пример. Пусть даны три отрасли, потребляющие и производящие, и дана конечная продукция по трём отраслям. Промежуточное потребление по каждой отрасли соответственно представлено в таблице. Найти объём валовой продукции каждой отрасли, а также матрицу А коэффициентов прямых материальных затрат и матрицу коэффициентов полных материальных затрат.
Производящие отрасли |
Потребляющие отрасли |
Конечная продукция Yi |
Валовая продукция Xi |
||
1 |
2 |
3 |
|||
1 |
200 |
50 |
300 |
200 |
750 |
2 |
150 |
250 |
10 |
100 |
510 |
3 |
230 |
50 |
150 |
300 |
730 |
Условно чистая продукция |
170 |
160 |
270 |
600 |
|
Xi |
750 |
510 |
730 |
|
|
Решение.
![]()
Х1=200+50+300+200=750;
Х2=150+250+10+100=510;
Х3=230+50+150+300=730.
Матрица А коэффициентов прямых
материальных затрат состоит из
коэффициентов аij,
смысл которых заключается в том, что
для производства продукции в j-ой отрасли,
![]() требуется определённое количество
затрат промежуточной продукции в i-ой
отрасли, равное аij.
требуется определённое количество
затрат промежуточной продукции в i-ой
отрасли, равное аij.
![]()
![]()
![]()
![]()

Эта матрица показывает, сколько потреблено промежуточной продукции. Матрица коэффициентов полных материальных затрат В=(I-А)-1. Вычислим её.

![]() ,
,
![]() .
.
![]()
![]()
![]()
Следовательно,
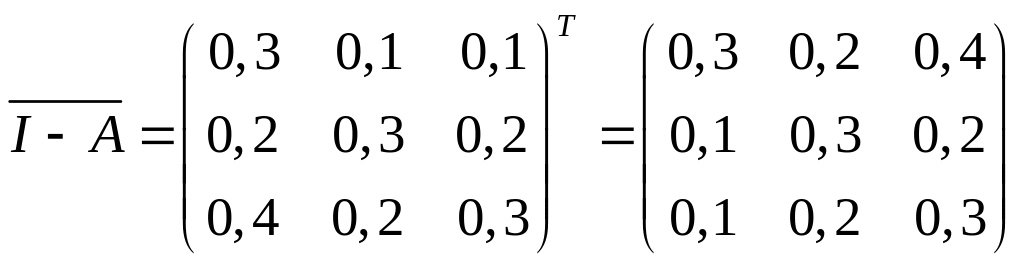 .
Откуда:
.
Откуда:
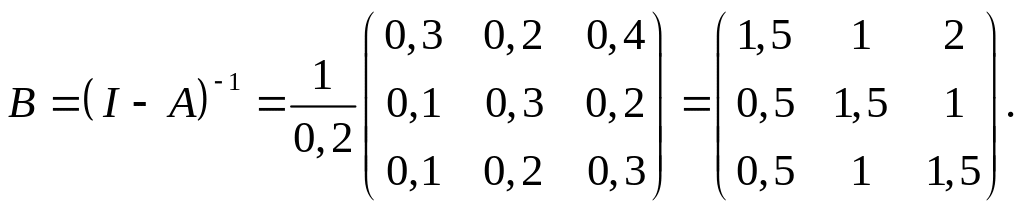
Модель Неймана.
Рассмотрим более общую модель Неймана. Рассмотрим экономику, описываемую парой (С, К), где С – пространство товаров, а К – множество производственных процессов, перерабатывающих некоторые количества товаров в другие количества тех же товаров. Под товаром (продуктом) понимаем как первичные факторы производства (земля, труд) и сырьё (нефть, уголь), так и конечные продукты производства, услуги и т.п. Будем считать, что имеется n различных товаров, количество i-го товара обозначается xi, тогда некоторый набор товаров обозначается X=(x1,,xn), т.е. является n-мерным вектором. Т.к. количества товаров неотрицательны, то для любого i=1,,n xi0 или X0. Множество всех наборов товаров называется пространством товаров С. Это множество называется пространством потому, что в нём можно сложить любые два набора и умножить любой набор товаров на любое неотрицательное число. Возможность умножения набора товаров на любое неотрицательное число отражает предположение о безграничной делимости и умножении товаров (т.е. товары устроены наподобие сахарного песка, а не авианосцев).
Предполагаем, что каждый товар имеет цену. Все цены предполагаются строго положительными. Пусть цена единицы i-го товара есть pi, тогда вектор P=(p1,,pn) есть вектор цен.
Набор товаров, как вектор, имеет ту же размерность, что и вектор цен. Для набора товаров X=(xi) и вектора цен P=(pi) их скалярное произведение PX= =p1x1++pnxn есть число, называемое ценой набора или его стоимостью.
Множество К производственных процессов имеет в своей основе конечное число процессов (Q1,,Qm), которые называются базисными. Каждый базисный процесс представляет собой пару векторов Qj=(,Bj) из С. (Векторы Aj, Bj – это векторы-столбцы. Содержательный смысл процесса Qj таков: он затрачивает вектор Аj=(aij) и выпускает вектор Bj=(bij), т.е. перерабатывает вектор Аj в вектор Bj. По смыслу все векторы Aj, Bj неотрицательны. Обозначив А=(А1,,Аm), B=(B1,,Bm), получаем, что технология нашей модели задаётся парой неотрицательных матриц A, B; матрица A называется матрицей затрат, B – матрицей выпуска.
Комбинируя базисные процессы, можно
получить новые процессы. Так, возьмём
неотрицательные числа zi,
i=1,,m,
и определим новый производственный
процесс z1Q1++zmQm,
в котором затраты есть вектор
![]() ,
а выпуск есть вектор
,
а выпуск есть вектор
![]() ;
полученный производственный процесс
кратко обозначим (AZ, BZ). Вектор-столбец
Z=(zi)
называется вектором интенсивностей.
Получившееся более широкое множество
процессов и обозначим К.
;
полученный производственный процесс
кратко обозначим (AZ, BZ). Вектор-столбец
Z=(zi)
называется вектором интенсивностей.
Получившееся более широкое множество
процессов и обозначим К.
Можно заметить, что в то время как базисные процессы Q1,,Qm соответствуют, вообще говоря, реальным отраслям, заводам, фабрикам, каждый элемент (X, Y)K есть некоторый фиктивный процесс, описывающий определённый режим совместной работы этих отраслей, заводов, фабрик. При этом X есть вектор затрат, Y – вектор выпуска.
Рассмотренная ранее модель Леонтьева есть частный случай модели Неймана при n=m, B=I. Основное отличие модели Неймана состоит в том, что всякий базисный процесс может выпускать не один продукт. Модель Неймана линейна.
Пример. Решим стандартную задачу
на модель Неймана. Даны матрицы
![]() ,
,
![]() технологических процессов, вектор цен
P=(1, 5) и вектор начальных запасов
технологических процессов, вектор цен
P=(1, 5) и вектор начальных запасов
![]() Найдём интенсивности технологических
процессов, максимизирующие стоимость
выпуска продукции за один производственный
цикл, и эту самую максимальную стоимость.
Найдём интенсивности технологических
процессов, максимизирующие стоимость
выпуска продукции за один производственный
цикл, и эту самую максимальную стоимость.
Решение. Пусть
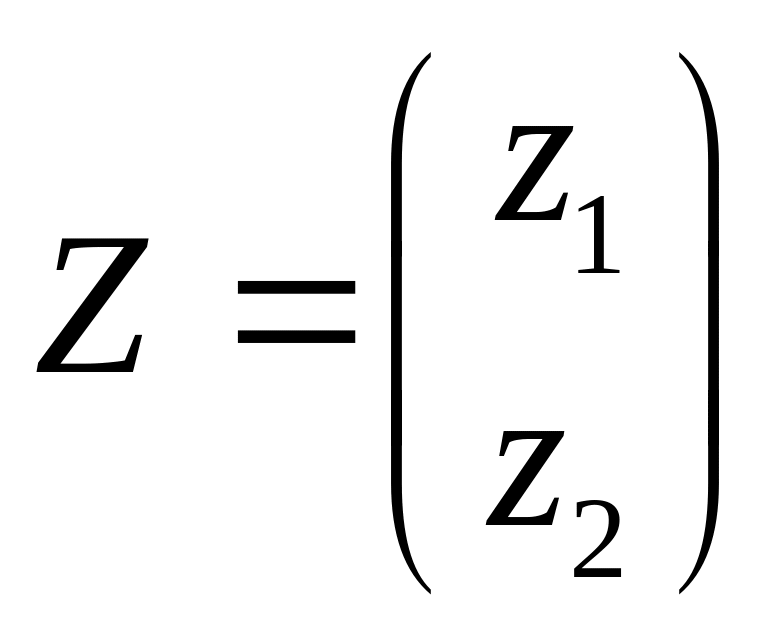 - вектор-столбец искомых интенсивностей,
тогда для их нахождения имеем задачу
линейного программирования:
- вектор-столбец искомых интенсивностей,
тогда для их нахождения имеем задачу
линейного программирования:
![]()
AZS
Z0
или (в развёрнутой форме)
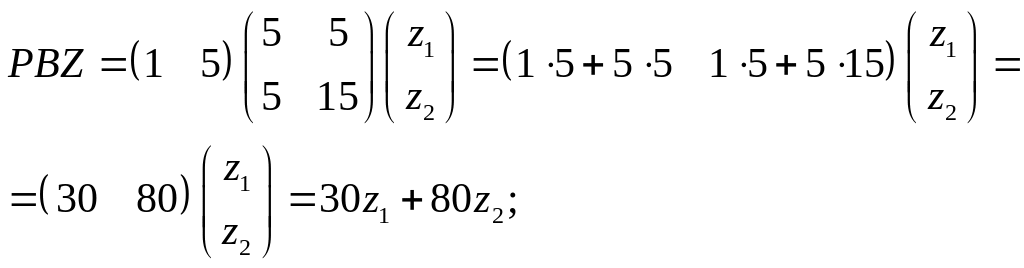
30z1+80z2max
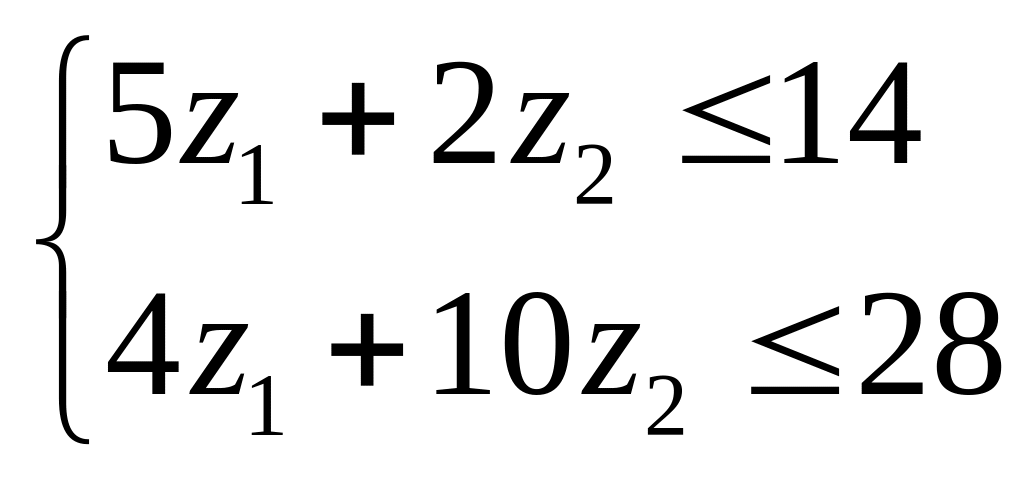
z1, z2 0.
Решим эту задачу графическим методом.
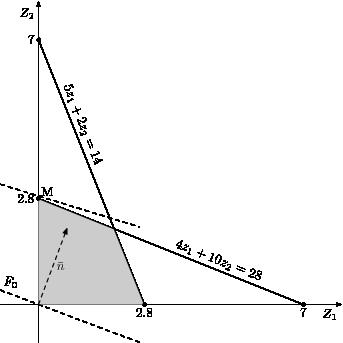
Рис.21. Графический метод решения задачи на модель Неймана
Найдём координаты точки максимума.
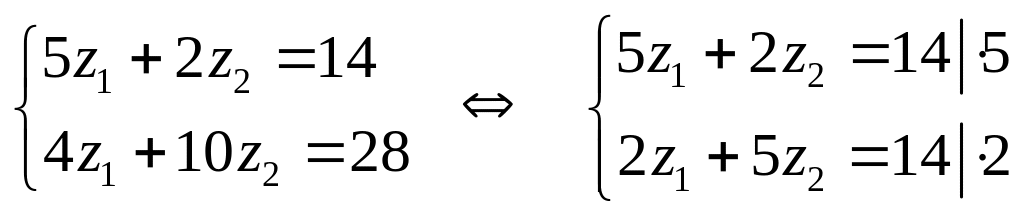 -
-
Откуда 21z1=42. Следовательно, z1=2 и z2=2.
Точка максимума (2, 2) и максимальная стоимость продукции, которая может быть выпущена за один цикл, равна 220.
