2. Определитель n-го порядка.

2.1. Определение. Вычисление определителей 2 и 3-го порядков.

Определение. Перестановкой J n-го порядка называется всякое расположение n чисел 1, 2, , n.

Общее число всех перестановок n-го порядка равно (читается эн-факториал).

В общем виде перестановку записывают в виде вектор-строки: J=(j₁ j₂  j_n). Перестановка (1 2  n) называется нормальной.

Беспорядком или инверсией в перестановке J называется наличие пары чисел, в которой большее число предшествует меньшему.

Число инверсий в перестановке J обозначим r(J). Если это чётное, то перестановка называется чётной, иначе – нечётной.

Определение 1. Определителем (детерминантом) n-го порядка квадратной матрицы A называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по одному из каждой строки и каждого столбца, причём знак каждого члена определяется как (-1)^r(J), где r(J) – число инверсий в перестановке J из номеров столбцов элементов матрицы (j₁ j₂  j_n), если при этом номера строк записаны в порядке возрастания:

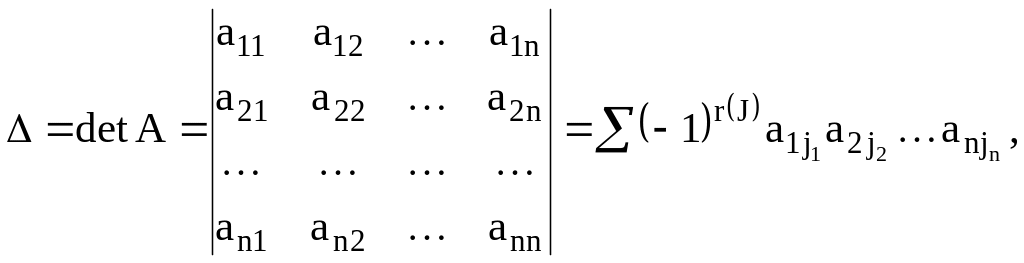где сумма берётся по всем перестановкам J.

Определители второго и третьего порядков.

Пусть n=2. Существует 2!=12=2 перестановки номеров столбцов матрицы

.

Составим перестановки номеров столбцов

J₁=(1 2) r(J₁)=0 J₂=(2 1) r(J₂)=1

(1 2)

Тогда, по определению 1,

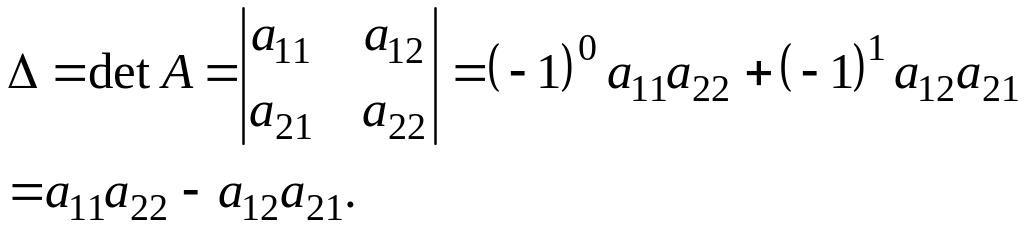
Мнемоническое правило: определитель второго порядка равен разности произведения элементов главной диагонали и произведения элементов побочной диагонали.

Пример.

Пусть n=3. Существует 3!=123=6 перестановок номеров столбцов.

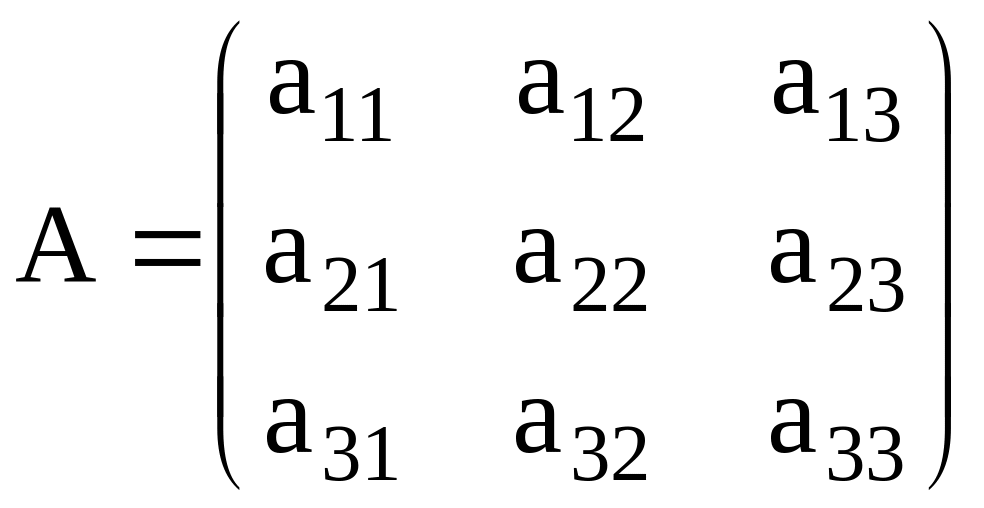
J1=(1 2 3) r(J1)=0	J3=(2 1 3) r(J3)=1 (1 2 3)	J5=(3 1 2) r(J5)=2 (1 3 2) (1 2 3)
J2=(1 3 2) r(J2)=1 (1 2 3)	J4=(2 3 1) r(J4)=1 (2 1 3) (1 2 3)	J6=(3 2 1) r(J6)=3 (2 3 1) (2 1 3) (1 2 3)

Тогда, по определению 1 имеем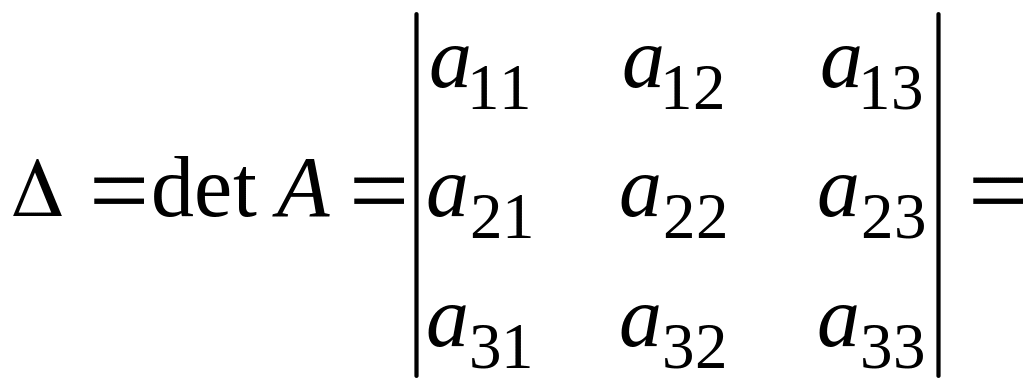

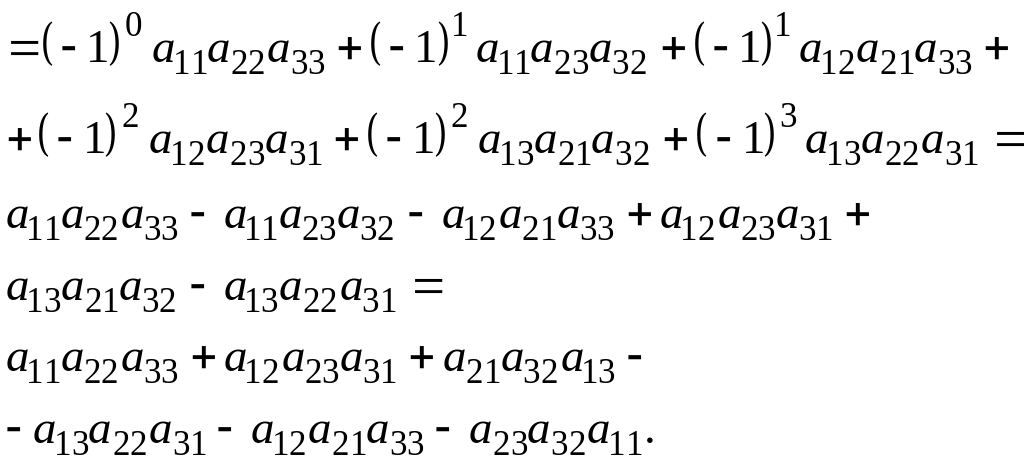
Правило Сарруса.

Определитель третьего порядка равен алгебраической сумме шести тройных произведений элементов, взятых по одному из каждой строки и каждого столбца соответствующей матрицы; со знаком + берутся произведения, сомножители которых находятся на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали; со знаком

- берутся произведения, сомножители которых стоят на побочной диагонали и в вершинах треугольников с основаниями, параллельными этой диагонали (см. рис.6.).

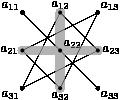
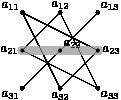
Рис. 6.Произведение элементов матрицы со знаком «+» или «-»

Пример.

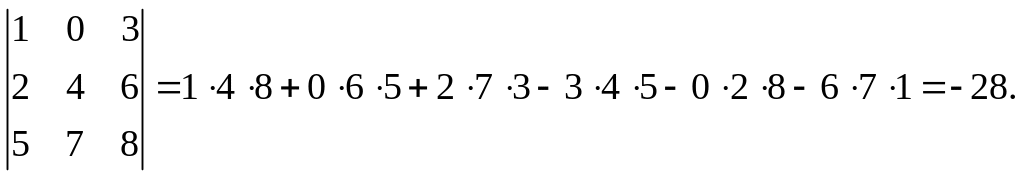
Существует также другое мнемоническое правило Сарруса вычисления определителя третьего порядка: приписать к определителю справа два первых столбца, не меняя их, и составить сумму произведений элементов главной диагонали и элементов, параллельных ей, из которой затем вычесть сумму произведений элементов побочной диагонали и элементов, параллельных ей:

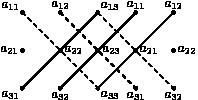
Рис.7. Другое правило Сарусса

На рисунке 7 пунктиром показаны произведения со знаком плюс, а сплошной линией – со знаком минус:

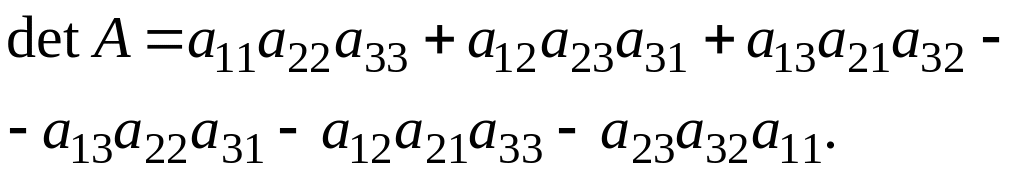
Для предыдущего примера: