
- •Введение
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов
- •1. Элементы теории множеств и комплексных чисел
- •1.1. Понятие множества. Операции над множествами
- •1.2. Числовые множества и их свойства.
- •2. Алгебра многочленов.
- •Глава 2. Матрицы. Определители
- •1. Алгебра матриц.
- •Виды матриц.
- •2. Определитель n-го порядка.
- •2.1. Определение. Вычисление определителей 2 и 3-го порядков.
- •2.2.Миноры и алгебраические дополнения.
- •2.3.Свойства определителя n-го порядка.
- •3. Действия над матрицами.
- •3.1.Линейные операции над матрицами.
- •3.2. Умножение матриц.
- •3.3. Многочлены от матриц.
- •3.4. Обратная матрица.
- •Вычисление обратной матрицы (через алгебраические дополнения).
- •3.5. Линейная зависимость строк и столбцов матрицы.
- •3.6. Ранг матрицы. Базисный минор.
- •3.7 Нахождение ранга матрицы
- •Вопросы для повторения.
- •Глава 3. Системы линейных уравнений и методы их решения.
- •1. Основные понятия и определения
- •2. Условия совместности системы линейных уравнений
- •3. Метод обратной матрицы
- •4. Правило Крамера
- •5. Метод Гаусса исключения неизвестных
- •7. Метод полного исключения
- •7.1. Решение систем линейных уравнений
- •7.2. Вычисление обратной матрицы методом полного исключения.
- •7.3. Вычисление ранга матрицы методом полного исключения
- •8. Собственные значения и собственные векторы матриц
- •9. Квадратичные формы
- •10. Численные методы решения систем линейных уравнений
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 4. Векторная алгебра
- •Векторное произведение двух векторов.
- •Вопросы для повторения.
- •Глава 5. Задачи линейного программирования
- •5.1. Постановка задачи линейного программирования (злп)
- •5.2. Графический метод решения злп
- •5.3. Симплекс – метод решения злп
- •Глава 6. Балансовые модели
- •6.1. Экономико-математическая модель (эмм) межотраслевого стоимостного баланса (модель Леонтьева)
- •Модель международной торговли
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Библиографический список
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов 4
- •Глава 2. Матрицы. Определители 17
- •Глава 3. Системы линейных уравнений и методы их решения. 51
- •Глава 4. Векторная алгебра 95
- •Глава 5. Задачи линейного программирования 110
- •Глава 6. Балансовые модели 128
10. Численные методы решения систем линейных уравнений
Нормы матриц.
Нормой
квадратной матрицы
порядка n
называется число, обозначаемое
![]() и удовлетворяющее
свойствам:
и удовлетворяющее
свойствам:
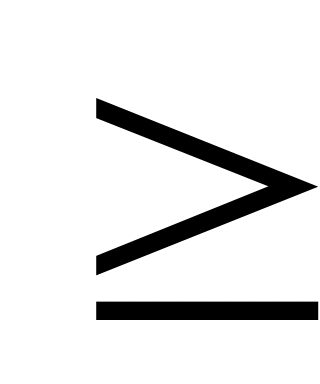 0,
=0
0,
=0
 A=;
A=; =
,
R;
=
,
R; ;
; .
.
Нормы матриц широко используются для оценки погрешностей итерационных методов решения задач линейной алгебры.
Канонические нормы матриц.
m-норма
 (берутся
суммы модулей элементов по строкам и
выбирается максимальная из них).
(берутся
суммы модулей элементов по строкам и
выбирается максимальная из них).l-норма
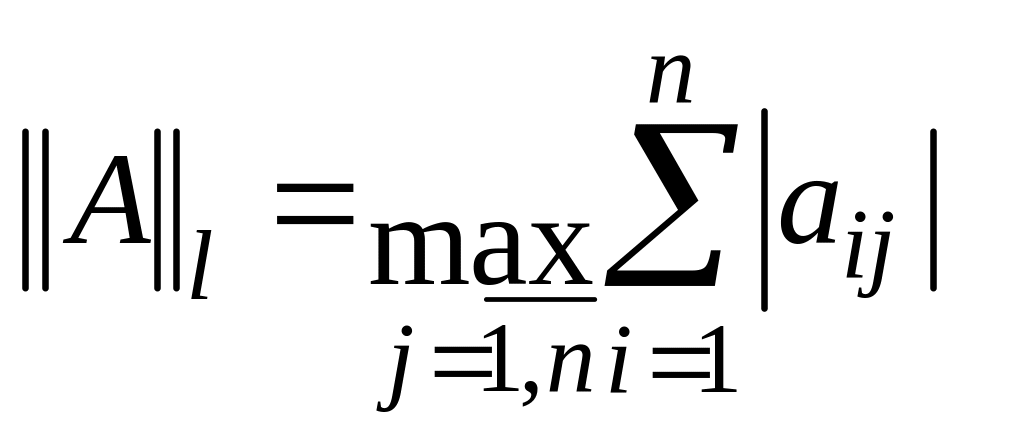 (берутся
суммы модулей элементов по столбцам и
выбирается максимальная из них).
(берутся
суммы модулей элементов по столбцам и
выбирается максимальная из них).k-норма
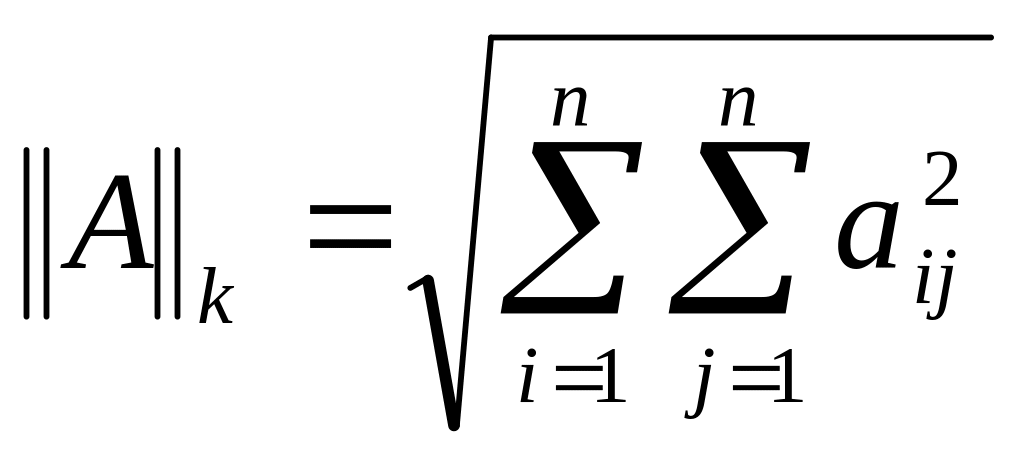 (евклидова
норма).
(евклидова
норма).
Диагональное преобладание.
В прикладных задачах часто приходится сталкиваться с линейными системами, при решении которых можно не заботиться о вредном воздействии неустранимых погрешностей на решение, спокойно применяя простейшую схему гауссова исключения (без выбора главного элемента). Это системы, для матриц которых выполнено условие диагонального преобладания:
![]() .
.
Это условие остаётся справедливым после каждого шага исключений в процессе приведения матрицы к треугольному виду, т.е.
![]() .
.
Это означает, что перед каждым исключением неизвестной разрешающий элемент будет находиться на главной диагонали.
Обусловленность системы.
Источником неустранимой погрешности решения системы линейных уравнений являются не только округления при выполнении вычислительных операций, но также ошибки, содержащиеся в исходных данных.
Пусть вместо системы
AX=f (1)
решается задача
(A+A)(X+X)=f+f, (2)
где A – матрица возмущений, моделирующих ошибки коэффициентов исходных уравнений (1), f – возмущения правых частей, X – обусловленный этими возмущениями вектор-столбец ошибок, отличающий решение системы (2) от решения системы (1). Тогда для относительной погрешности решения справедлива оценка:
![]() ,
(3)
,
(3)
где
A=CondA=![]() .
Значение
A
называется
числом обусловленности
матрицы
A.
Оно определяет, насколько сильно
погрешности входных данных могут
повлиять на решение системы. Всегда
A1.
Если 1<A<10,
ошибки входных данных слабо сказываются
на решении, система (1) называется хорошо
обусловленной.
Если A103,
система (1) плохо
обусловлена,
решение её сильно зависит от ошибок в
правых частях и коэффициентах.
.
Значение
A
называется
числом обусловленности
матрицы
A.
Оно определяет, насколько сильно
погрешности входных данных могут
повлиять на решение системы. Всегда
A1.
Если 1<A<10,
ошибки входных данных слабо сказываются
на решении, система (1) называется хорошо
обусловленной.
Если A103,
система (1) плохо
обусловлена,
решение её сильно зависит от ошибок в
правых частях и коэффициентах.
Пример. Рассмотрим систему:
![]()
Её решение x1=x2=1.
Исказим теперь слегка её правые части.
![]() .
.
Решение искажённой системы: x1=2,97, x2=-0,99. Чтобы сопоставить полученные результаты с оценкой (3), будем пользоваться m-нормой.
![]() .
.
Относительная
погрешность
![]() .
Это очень малая величина.
.
Это очень малая величина.
Далее,
![]() .
.
![]() =9800-9801=
-1
=9800-9801=
-1![]() 0;
0;
![]() .
.
![]() max(-98+99;99+-100)=max(197;199).
max(-98+99;99+-100)=max(197;199).
A=![]() .
.
Согласно
(3)
![]() ,
что, как видно, согласуется с результатами
решения рассмотренных систем.
,
что, как видно, согласуется с результатами
решения рассмотренных систем.
Метод итераций приближённого решения системы линейных уравнений.
При большом числе неизвестных схемы, дающие точное решение, становятся очень сложными. Удобней пользоваться приближёнными методами.
Пусть дана система линейных уравнений:
![]() .
.
Допустим,
что все диагональные элементы aii0
![]() .
.
Систему разрешают относительно диагональных элементов:
x1 = 1+12 x2+13 x3+…+1n xn
x2 = 2+21 x1+23 x3+…+2n xn
………………………………………………………
xn = n+n1 x1+n2 x2+…+n-1,n xn,
где
![]() .
.
Получаем
другую матрицу
![]() порядка
nn
и столбец свободных членов
порядка
nn
и столбец свободных членов
![]() .
.
Полученную систему линейных уравнений X=+X будем решать методом последовательных приближений. За нулевое приближение принимаем столбец свободных членов: X(0)= . Далее, последовательно строим вектор-столбцы
X(1)= +X(0) (1-ое приближение),
X(2)= +X(1) (2-ое приближение), и т.д.
X(k+1)= +X(k) ((k+1)-ое приближение).
Запишем формулы приближений в развёрнутом виде:
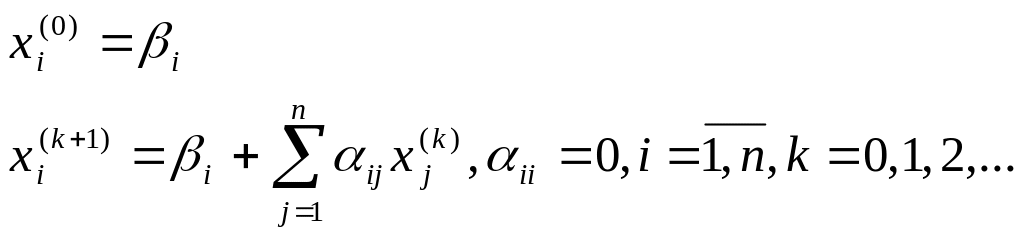
Метод последовательных приближений, определяемый этими формулами, называется методом итераций.
На
практике вычисления проводят до тех
пор, пока
![]() ,
где
- требуемая точность вычислений.
,
где
- требуемая точность вычислений.
Этот
метод хорошо сходится, т.е. число
приближений, необходимых для получения
корней системы линейных уравнений с
заданной точностью невелико, если
![]() ,
малы по абсолютной величине, т.е. модули
диагональных коэффициентов матрицы A
должны быть малы по сравнению с модулями
недиагональных элементов этой матрицы
(свободные члены при этом роли не играют).
,
малы по абсолютной величине, т.е. модули
диагональных коэффициентов матрицы A
должны быть малы по сравнению с модулями
недиагональных элементов этой матрицы
(свободные члены при этом роли не играют).
Сходящийся процесс итераций обладает свойством самоисправляемости, т.е. отдельная ошибка в вычислениях не отражается на окончательном результате, т.к. ошибочное приближение можно рассматривать как новый начальный вектор.
Достаточное условие сходимости метода итераций.
Процесс
итераций для приведённой системы
линейных уравнений сходится к единственному
её решению, если какая-нибудь каноническая
норма матрицы
меньше 1, т.е. для итерационного процесса
X(k)=+X(k-1)
(k=1,
2, …) (X(0)
– произвольно) достаточное условие
сходимости есть
![]() .
.
Пример. Методом итераций решить систему линейных уравнений с точностью = 0,001.
![]() .
.
Решение.
Разрешим систему относительно диагональных
элементов.
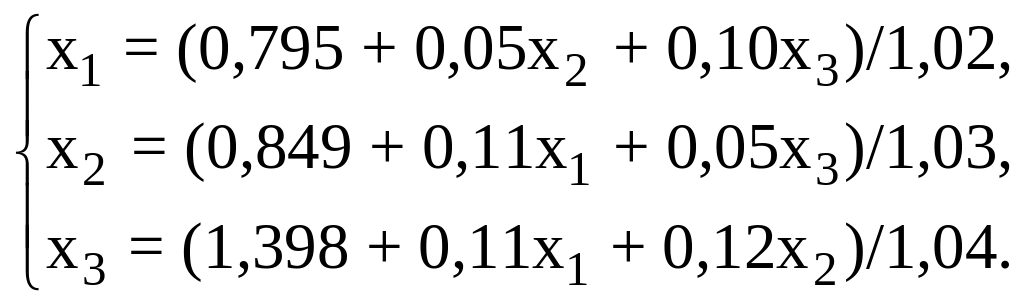
То
есть
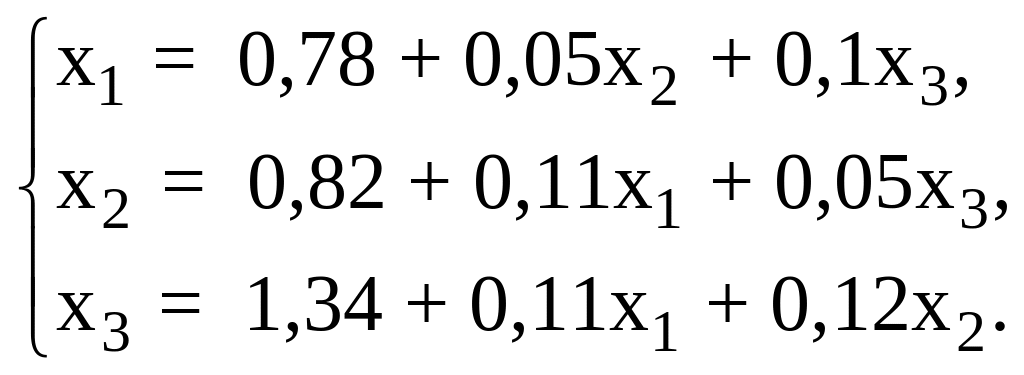 (4)
(4)
или в матричном виде X=+X, где
![]() .
.
Проверим выполнение достаточного условия сходимости метода итераций.
![]()
![]() .
.
Подставив нулевое приближение в систему (4), получим первое приближение:
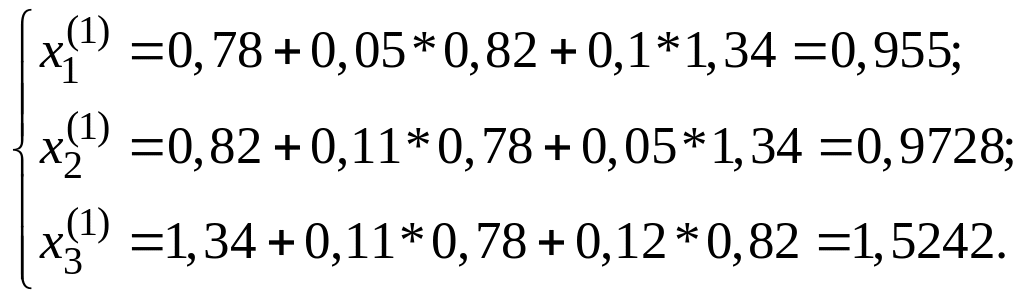
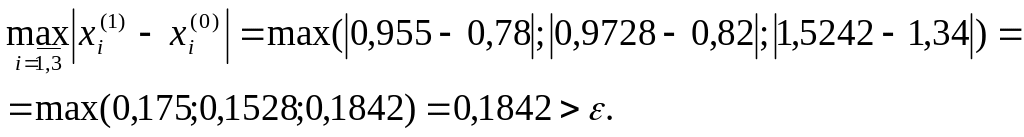
Строим 2-ое приближение, подставив в систему (1) первое приближение и т.д., до тех пор, пока не достигнем требуемой точности.

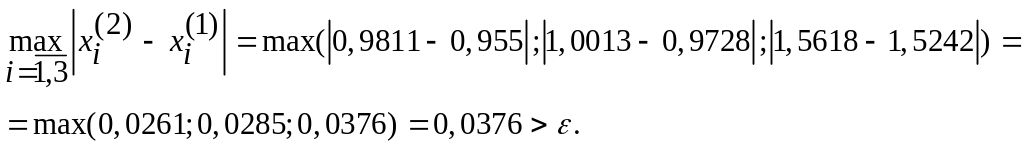

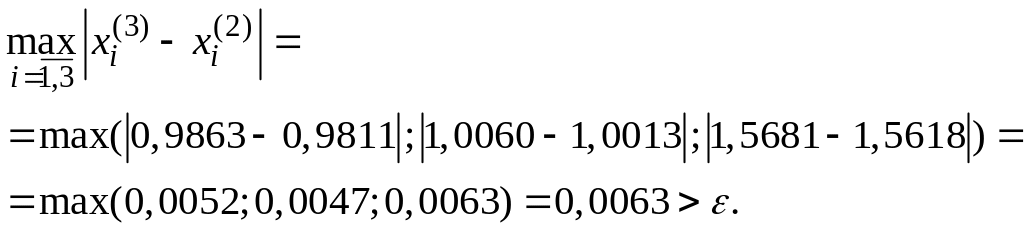
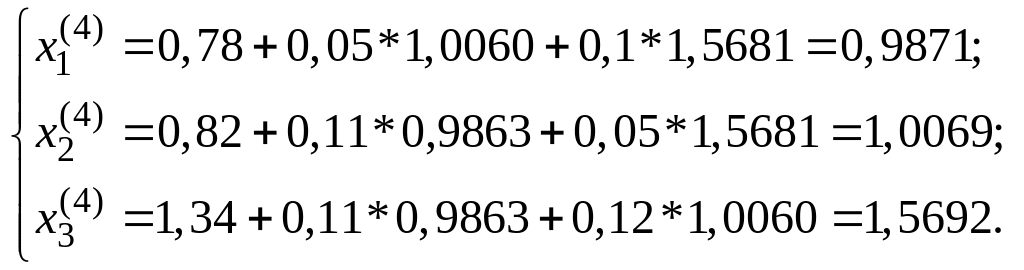
![]()
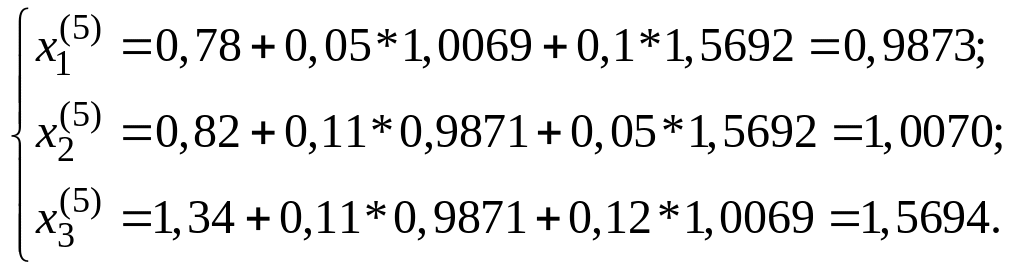
![]()
Итак,
![]()
