- •Введение
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов
- •1. Элементы теории множеств и комплексных чисел
- •1.1. Понятие множества. Операции над множествами
- •1.2. Числовые множества и их свойства.
- •2. Алгебра многочленов.
- •Глава 2. Матрицы. Определители
- •1. Алгебра матриц.
- •Виды матриц.
- •2. Определитель n-го порядка.
- •2.1. Определение. Вычисление определителей 2 и 3-го порядков.
- •2.2.Миноры и алгебраические дополнения.
- •2.3.Свойства определителя n-го порядка.
- •3. Действия над матрицами.
- •3.1.Линейные операции над матрицами.
- •3.2. Умножение матриц.
- •3.3. Многочлены от матриц.
- •3.4. Обратная матрица.
- •Вычисление обратной матрицы (через алгебраические дополнения).
- •3.5. Линейная зависимость строк и столбцов матрицы.
- •3.6. Ранг матрицы. Базисный минор.
- •3.7 Нахождение ранга матрицы
- •Вопросы для повторения.
- •Глава 3. Системы линейных уравнений и методы их решения.
- •1. Основные понятия и определения
- •2. Условия совместности системы линейных уравнений
- •3. Метод обратной матрицы
- •4. Правило Крамера
- •5. Метод Гаусса исключения неизвестных
- •7. Метод полного исключения
- •7.1. Решение систем линейных уравнений
- •7.2. Вычисление обратной матрицы методом полного исключения.
- •7.3. Вычисление ранга матрицы методом полного исключения
- •8. Собственные значения и собственные векторы матриц
- •9. Квадратичные формы
- •10. Численные методы решения систем линейных уравнений
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Глава 4. Векторная алгебра
- •Векторное произведение двух векторов.
- •Вопросы для повторения.
- •Глава 5. Задачи линейного программирования
- •5.1. Постановка задачи линейного программирования (злп)
- •5.2. Графический метод решения злп
- •5.3. Симплекс – метод решения злп
- •Глава 6. Балансовые модели
- •6.1. Экономико-математическая модель (эмм) межотраслевого стоимостного баланса (модель Леонтьева)
- •Модель международной торговли
- •Вопросы для повторения.
- •Задачи для самостоятельного решения.
- •Библиографический список
- •Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов 4
- •Глава 2. Матрицы. Определители 17
- •Глава 3. Системы линейных уравнений и методы их решения. 51
- •Глава 4. Векторная алгебра 95
- •Глава 5. Задачи линейного программирования 110
- •Глава 6. Балансовые модели 128
2. Алгебра многочленов.
Определение.
Многочленом
степени n
с действительными коэффициентами
![]() называется выражение вида:
называется выражение вида:
![]()
Два многочлена равны, если равны их коэффициенты при одинаковых степенях x.
Число x= называется корнем многочлена Pn(x), если Pn()=0.
Теорема.
Пусть An(x)
и Bm(x)
– многочлены от x,
![]() n>m.
Тогда существуют такие многочлены
Qn-m(x)
и Rk(x),
n>m.
Тогда существуют такие многочлены
Qn-m(x)
и Rk(x),
![]() что
что
An(x)= Bm(x) Qn-m(x) + Rk(x),
причём k<m. При этом под многочленом нулевой степени R0(x) понимается действительное число.
Многочлены Qn-m(x) и Rk(x), обладающие этими свойствами, называются соответственно неполным частным (или частным, если Rk(x)=0) и остатком при делении An(x) на Bm(x).
Пример. Разделим многочлен A4(x)=2x4-3x3+2x-8 на многочлен B1(x)=x-2 уголком (см. рис. 5.)
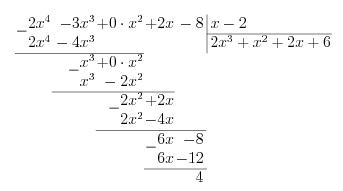
Рис.5. Деление многочлена на многочлен уголком
Получили частное Q3(x)= 2x3+x2+2x+6 и остаток R0(x)=4.
Таким образом, получили разложение
2x4-3x3+2x-8=(x-2)(2x3+x2+2x+6)+4.
Теорема Безу. Остаток от деления многочлена Pn(x) на двучлен x- равен Pn().
Следствие. Число является корнем многочлена Pn(x) тогда и только тогда, когда Pn(x) делится без остатка на x-.
Для нашего примера A4(2)=216-38+22-8=4=R0(x) – остаток.
Теорема.
Если многочлен
с целыми коэффициентами Pn(x)=![]() имеет
рациональный корень
имеет
рациональный корень
![]() ,
то p является делителем свободного члена
an,
а q
является делителем коэффициента при
старшем члене a0.
,
то p является делителем свободного члена
an,
а q
является делителем коэффициента при
старшем члене a0.
Определение.
Если многочлен Pn(z)
степени
![]() с
действительными коэффициентами
делится на (z-z0)k,
с
действительными коэффициентами
делится на (z-z0)k,
![]() ,
и не делится на (z-z0)k+1,
то число k называется кратностью корня
z0
многочлена Pn(z).
,
и не делится на (z-z0)k+1,
то число k называется кратностью корня
z0
многочлена Pn(z).
Теорема.
Если комплексное число z0
является корнем кратности k многочлена
Pn(z)
с действительными коэффициентами, то
и сопряжённое ему число
![]() также является корнем кратности k этого
многочлена.
также является корнем кратности k этого
многочлена.
Основная теорема алгебры. Каждый многочлен степени имеет в точности n корней, вообще говоря, комплексных, если каждый корень считать столько раз, какова его кратность.
Глава 2. Матрицы. Определители
1. Алгебра матриц.
Определение.
Матрицей
размера m×n
называется прямоугольная таблица чисел,
содержащая m
строк и n
столбцов. Числа, составляющие матрицу,
называются её элементами.
Элементы матрицы A обозначаются как
aij,
где i
– номер строки, j – номер столбца, на
пересечении которых расположен данный
элемент,
![]()
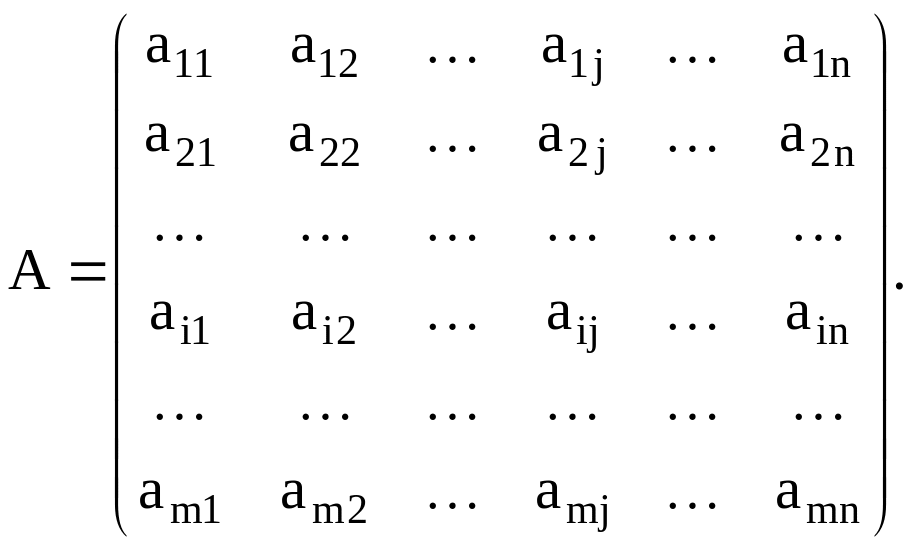
Часто
матрицу A записывают в сокращённом виде:
![]() или
или
![]() ,
где
,
где![]()
Виды матриц.
Квадратная: m=n.

Число n называется порядком матрицы.
Упорядоченная совокупность элементов a11, a22, , ann называется главной диагональю квадратной матрицы, а упорядоченная совокупность элементов a1n, a2,n-1, , an1 – побочной диагональю.
Сумма элементов главной диагонали квадратной матрицы A называется следом (шпуром) матрицы A:
![]()
Верхняя
треугольная матрица
– матрица, у которой элементы aij=0
при i>j,
![]()
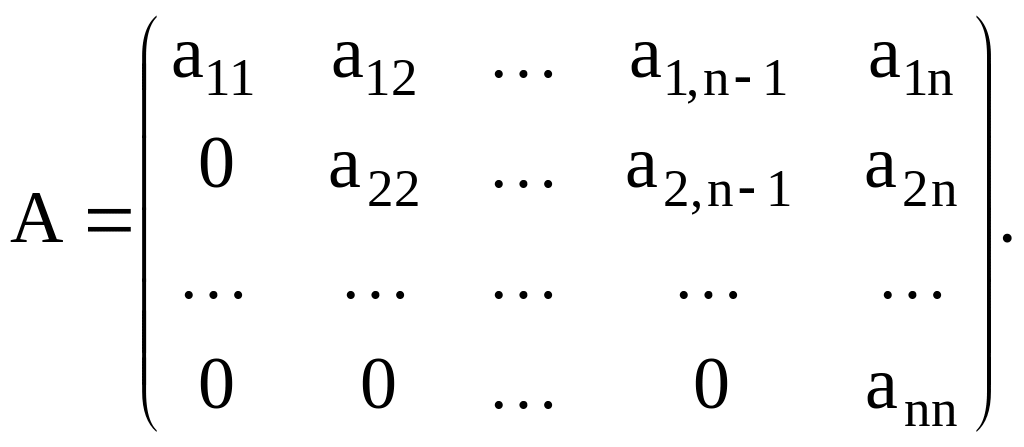
Нижняя треугольная матрица – матрица, у которой элементы aij=0 при i<j,

Диагональная матрица - матрица, элементы которой удовлетворяют условию:
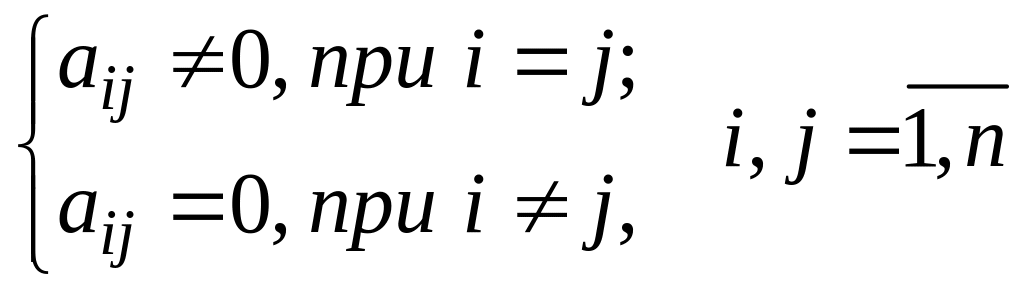
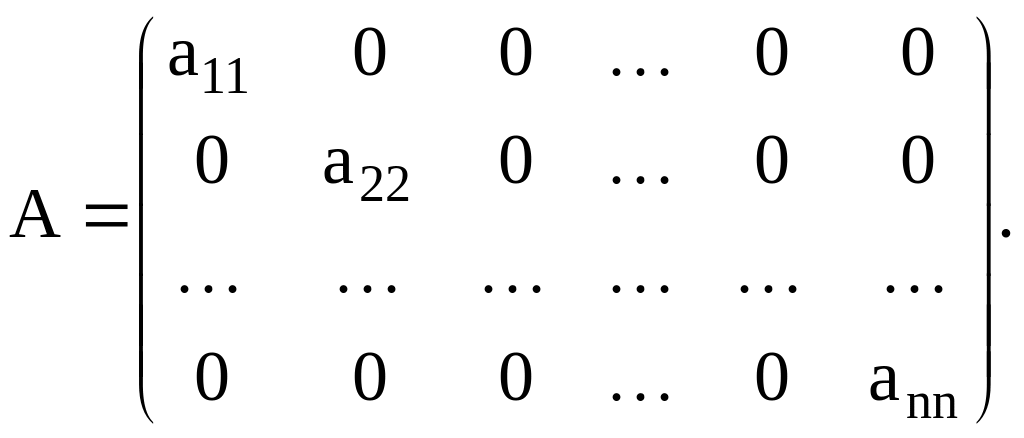
Единичная
матрица -
диагональная матрица, у которой все
элементы главной диагонали aii=0,
![]()

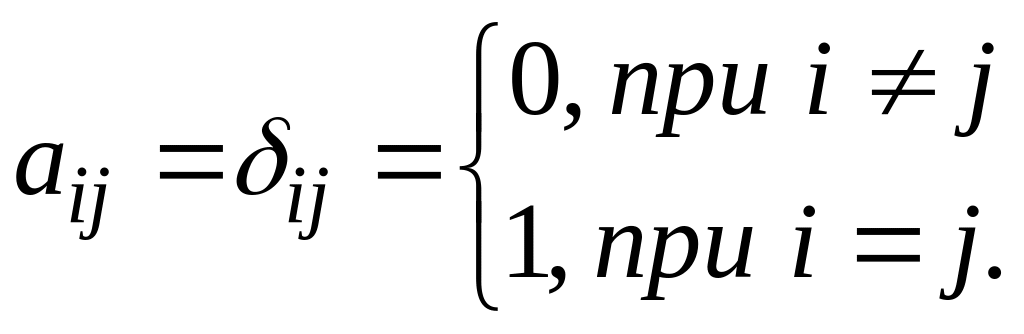
где
![]() - символ
Кронекера,
- символ
Кронекера,
![]() .
.
Симметрическая матрица - матрица, у которой все элементы aij=aji, В этом случае говорят, что элементы матрицы симметричны относительно главной диагонали.
Если
aij=-aji,
![]() ,
то матрица называется кососимметрической.
,
то матрица называется кососимметрической.
Нулевая матрица - матрица, у которой все элементы aij=0,

Матрица называется ступенчатой, если она имеет вид:
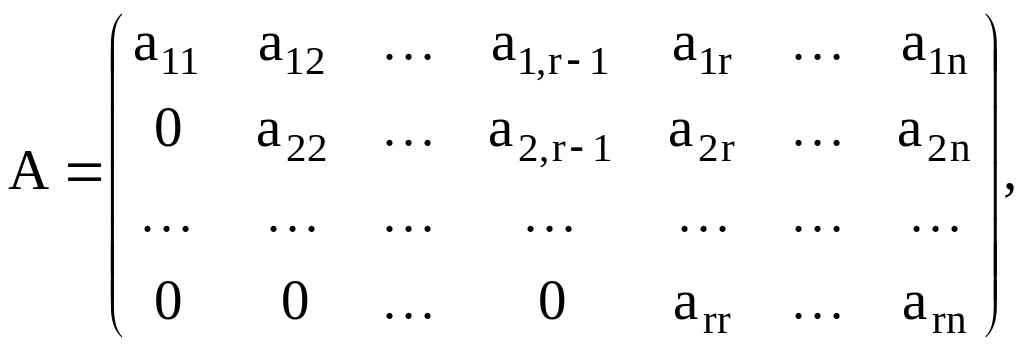
где
![]() ,
для всех
,
для всех
![]() .
.
Матрица, состоящая из одной строки, называется вектором-строкой, матрица, состоящая из одного столбца - вектором-столбцом.
Две матрицы A и B называются равными (A=B), если они имеют одинаковые размеры и их соответствующие элементы равны.
Матрица
![]() называется
транспонированной
к матрице
называется
транспонированной
к матрице
![]() ,
если bij=aji
,
если bij=aji
![]() Обозначение: B=AТ.
Обозначение: B=AТ.

Пример.