Модель международной торговли

С помощью модели международной торговли (другое её название – линейная модель обмена) можно определить, какими должны быть соотношения между государственными бюджетами стран, торгующих между собой, чтобы торговля была взаимовыгодной.

Рассмотрим модель международной торговли, в которой участвуют n стран. Обозначим:

x_i – национальный доход i-ой страны;

a_ij – доля национального дохода j-ой страны, которую она расходует на закупку товаров i-ой страны;

p_i – общая выручка от внутренней и внешней торговли для i-ой страны.

Предположим, что каждое государство расходует весь свой национальный доход на закупку товаров внутри страны и на импорт из других стран. Это означает, что

Матрица А, элементами которой являются коэффициенты a_ij, называется структурной матрицей торговли. Сумма элементов каждого столбца этой матрицы равна единице.

Предположим, что в течение определённого фиксированного промежутка времени структура международной торговли не меняется (не меняется структурная матрица торговли), а национальные доходы торгующих стран могут измениться.

Требуется определить, какими могут быть эти национальные доходы, чтобы сумма платежей всех государств была равна суммарной выручке от внешней и внутренней торговли.

Для любой страны выручка от внутренней и внешней торговли составит:

p_i=a_i1x₁+a_i2x₂++a_inx_n.

В сбалансированной системе международной торговли не должно быть дефицита, т.е. у каждой страны выручка от торговли должна быть не меньше её национального дохода:

p_ix_i,

Последнее неравенство справедливо только в случае, когда p_i=x_i, т.е. у всех торгующих стран выручка от внешней и внутренней торговли должна совпадать с национальным доходом.

В матричной записи это означает, что имеет равенство AX=X, где A - структурная матрица международной торговли, а X – вектор национальных доходов.

Вектор X является собственным вектором структурной матрицы торговли A, а соответствующее собственное значение равно единице. Отсюда следует, что баланс в международной торговле будет достигнут, если единица

является собственным значением структурной матрицы международной торговли, а вектор национальных доходов торгующих стран – собственным вектором, отвечающим этому единичному собственному значению.

Пример. Найти национальные доходы x₁, x₂, x₃ торгующих стран в сбалансированной системе международной торговли. Структурная матрица торговли трёх стран имеет вид:

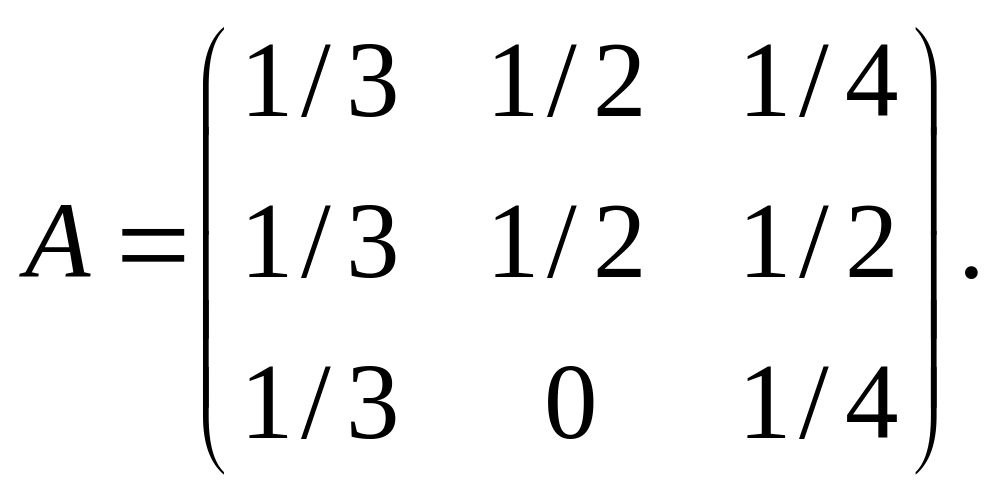
Решение. Найдём собственный вектор X, отвечающий собственному значению λ=1, решив уравнение (А-λI)X= Система уравнений имеет вид

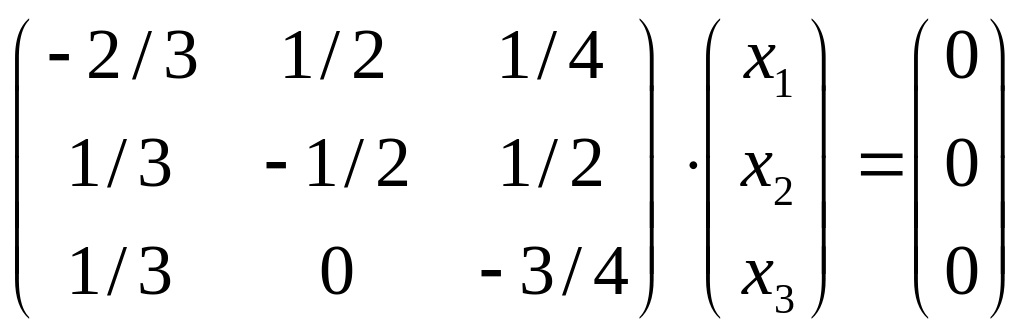или

Из третьего уравнения системы находим Из второго уравнения системы находим Подставляя выражения для x₁ и x₂ в первое уравнение системы, получим: или 0=0, т.е. тождество. Таким образом, получаем общее решение системы:

x₃=c, c=const.

Из приведённых вычислений видно, что сбалансированность торговли трёх стран достигается при векторе национальных доходов , т.е. при соотношении национальных доходов или 9:10:4.

Ответ. .