Введение

Это учебное пособие написано на основе лекций, читаемых авторами на инженерно-экономическом факультете ВГТУ по курсам «Математика» и «Линейная алгебра».

В пособии изложены необходимые основы математического аппарата и примеры его использования в современных экономических приложениях: элементы теории множеств, линейной и векторной алгебры, численных методов линейной алгебры, линейного программирования. Такой объём знаний актуален сегодня для студентов, получающих образование по экономическим специальностям, и соответствует требованиям государственных стандартов по экономическим специальностям.

Изложение материала проведено почти без доказательств – основной упор сделан на приобретение навыков использования математического аппарата. Каждый раздел сопровождается решением характерных задач и соответствующих экономических приложений. Приложения, представляющие в экономике самостоятельный интерес, выделены в отдельный раздел. Пособие содержит также подборку вопросов для повторения, задач и упражнений для самостоятельного решения по каждой теме.

Глава 1. ОСновные понятия теории множеств, комплексных чисел и алгебры многочленов

1. Элементы теории множеств и комплексных чисел

1.1. Понятие множества. Операции над множествами

Основателем современной теории множеств считается Георг Кантор. Множество является одним из основных, неопределяемых понятий математики. Оно может содержать конечное или бесконечное число объектов любой природы, однородных по некоторому признаку. Объекты множества называются его элементами. Если множество содержит конечное число элементов, то оно называется конечным множеством, иначе множество называется бесконечным.

Если x – элемент множества X, то пишут: (x принадлежит X). Если x не является элементом множества X, то пишут: (читают: x не принадлежит X). Запись означает, что множество X состоит из элементов .

Примеры множеств: множество студентов вуза, множество молекул в данном веществе и т.д.

Если множество не содержит ни одного элемента, то оно называется пустым множеством и обозначается .

Пусть X и Y – два множества. Если каждый элемент множества X является элементом множества Y, то множество X называется подмножеством множества Y и пишут: (X содержится в Y) или (Y содержит X).

Свойства подмножеств.

Для любого множества А:

1) ;

2) .

Множества A и B называются равными, если они состоят из одних и тех же элементов. Обозначение: . Ясно, что если и , то .

Всякое подмножество A данного множества B, которое не совпадает с B и , называется собственным подмножеством B: .

Операции над множествами.

Пусть даны два произвольных множества A и B.

Объединением множеств A и B называется множество C, состоящее из элементов множеств A и B. При этом пишут: . Легко видеть, что .

Пересечением множеств A и B называется множество C, состоящее из элементов, одновременно принадлежащих множеству A и множеству B. Обозначение: .

Разностью множеств A и B называется множество R=A\B, состоящее из элементов A, которых нет в B.

Геометрически операции над множествами изображаются с помощью диаграмм Эйлера-Венна (см. рис.1).

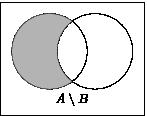
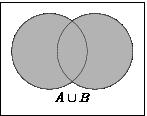
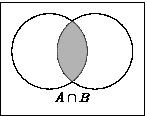
Рис.1.

Множество, рассматриваемое вместе с каким-нибудь установленным в нём порядком следования элементов, называется упорядоченным множеством и обозначается: .