II. Вероятность события
Рассматривая различные случайные события при выполнении одних и тех же условий , нетрудно убедиться в том, что каждое из них обладает какой-то степенью возможности: одни большей, другие - меньшей. Для того, чтобы количественно сравнивать между собой события по степени их возможности, очевидно необходимо с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое число назовем вероятностью события. Таким образом, вероятность события есть численная мера степени объективной возможности происхождения этого события в некоторых условиях. Будем говорить, что при выполнении комплекса условий G событие А происходит с вероятностью P(A).
Сравнивая между собой различные события по степени их возможности, мы должны установить какую-либо единицу измерения. В качестве такой единицы измерения естественно принять вероятность достоверного события, т. е. такого, которое в результате опыта непременно должно произойти. Если приписать достоверному событию вероятность, равную единице, то все другие события – возможные, но не достоверные – будут характеризоваться вероятностями, меньшими единицы, составляющими какую-то долю единицы. Противоположностью по отношению к достоверному событию является невозможное событие, т. е. такое, которое в данном опыте не может произойти. Естественно приписать невозможному событию вероятность, равную нулю. Таким образом,
.
1. Классическое определение вероятности
Для определения вероятности события существуют различные подходы. Классическое определение вероятности сводит понятие вероятности к понятию равновероятности или равновозможности событий, которое считается основным и не подлежит формальному определению. Под равновозможными понимаются события, которые в силу тех или других причин (например, симметрии) не имеют объективного преимущества одно перед другим.
Если событие А подразделяется на m частных случаев, входящих в полную группу, состоящую из n равновозможных, попарно несовместных событий, то вероятность события А определяется как
.
(2.1)
Иными словами можно сказать, что вероятностью события называется отношение числа исходов опыта, при которых наступает событие A, к общему числу возможных исходов опыта. При этом обязательным условием является равновозможость исходов опыта.
Пример 2.1. Правильная монета подбрасывается один раз. Найти вероятности событий: А = {появление герба}, В = {появление цифры}.
Решение.
В этом простейшем примере
,
А=
;
В=
,
где
;
.
Тогда по формуле (1.1)
.
Пример 2.2. Стандартная игральная кость брошена один раз. Каковы вероятности событий: А = {выпадения четного числа очков}, В = {выпадения числа очков, кратного трем}, С = {выпадение дробного числа очков}, D = {выпадение любого числа очков}.
Решение.
Пространство элементарных событий
,
где
= {выпадение i
очков,
i
= 1, 2,…,6},
.
Здесь А
=
,
=3;
В
=
,
;
С
=
,
;
D
=
,
.
По
классическому определению (1.1) получаем:
.
Классическое определение вероятности удобнее всего иллюстрировать на так называемой урновой модели. Рассмотрим примеры.
Пример 2.3. В урне находится 10 лотерейных билетов, из которых 4 выигрышные. Из урны, не глядя, наудачу вынимаются два билета. Найти вероятность того, что: а) оба билета выигрышные; б) оба билета без выигрыша; в) один билет выигрышный, а другой – нет.
Решение. Пусть A – событие, состоящее в том, что оба билета выигрышные; B – оба билета без выигрыша; С – один билет выигрышный, а другой – нет.
а)
Выбор двух билетов из десяти можно
осуществить n=
=45
способами, а двух выигрышных билетов
из четырех – m=
=6
способами. Тогда по формуле (2.1)
P(A)=6/45=2/15.
б)
Имеется m=C
=15
возможностей выбора билетов без выигрыша.
В этом случае вероятность P(B)=15/45=1/3.
в) Существует 4 возможности вытащить выигрышный билет и 6 возможностей – билет без выигрыша. Согласно основному принципу перечисления, имеется m=64=24 возможностей вытащить один билет с выигрышем, а другой – без выигрыша. Тогда P(C)=24/45=8/15.
Пример
2.4.
В партии из N
изделий имеется M
(M
N)
бракованных. Из партии наудачу выбирается
k
изделий. Определить вероятность того,
что среди этих k
изделий будет ровно r
(r
k)
бракованных (событие А).
Решение.
Число всех равновозможных исходов
определяется как n
=
.
Так как всего бракованных изделий M,
то число способов, которыми можно вынуть
r
из них, равно
.
Каждая такая совокупность из r
бракованных изделий будет дополняться
k
- r
годными изделиями, которые будут
выбираться из общего числа N
- M
годных изделий. Число способов выбора
таких совокупностей равно
.
Следовательно,
по правилу произведения комбинаторики,
число исходов, благоприятствующих
появлению события А,
равно
.
Отсюда
.
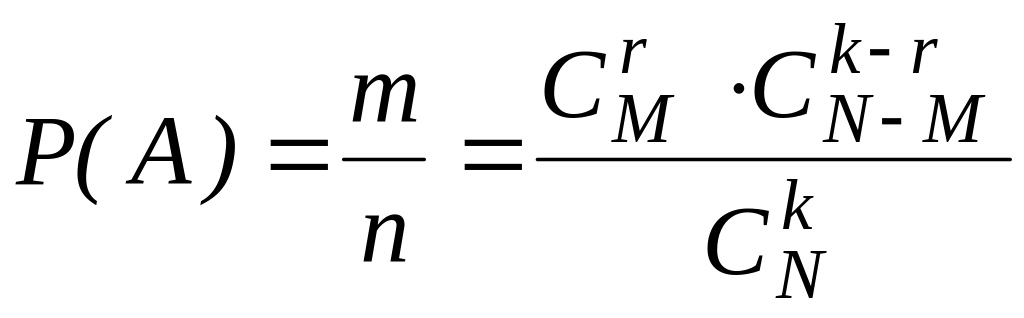Для наглядности описанная в задаче схема выбора изображена на рис. 1.
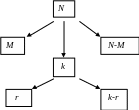
Рис.1
Классическое определение вероятности нельзя применить к опыту с бесконечным числом «равновероятных» исходов. В этом случае целесообразно переходить на геометрический язык и пользоваться геометрическим подходом к определению вероятности.