III. Основные теоремы теории вероятностей
В любых сколь угодно сложных расчетах по теории вероятностей в той или иной форме используют две теоремы: теорему сложения и теорему умножения вероятностей.
1. Теоремы сложения вероятностей
Теорема 1. Вероятность суммы конечного числа попарно несовместных событий равна сумме их вероятностей.
Если
несовместимые события, то вероятность
появления одного из событий
,
или
,
или …,
равна сумме вероятностей этих событий:
(3.1)
Если
несовместимые события
составляют полную группу, то одно из
них появляется обязательно и, следовательно,
Учитывая (3.1), получаем для полной группы
событий
(3.2)
Следствие. Если полная группа состоит из двух событий взаимно противоположных событий A и , то из (4.1) следует
.
(3.3)
Пример 3.1. Мишень состоит из концентрических окружностей. Вероятность попадания в первый, центральный круг - 0,05, во второй (средний) - 0,20 и наружное кольцо - 0,50. Какова вероятность попадания в мишень при одном выстреле?
Решение.
Искомое
событие A
произойдет, если произойдет хотя бы
одно из событий:
={попадание
в первый, центральный круг},
={попадание
в среднее кольцо},
=
{попадание в наружное кольцо}
,
т. е. событие A
представимо в виде суммы событий
,
причем слагаемые события в этой сумме
попарно несовместны и вероятности их
наступления заданы. Тогда по теореме
сложения получим
Пример 3.2. На экзамене 15 билетов разложены в случайном порядке, причем студент знает ответ только на 5 билетов. Преподаватель предложил студенту взять три билета. Найти вероятность того, что хотя бы один билет попадет студенту, на который он знает ответ.
Решение
1. Событие A
(хотя бы один билет из трех студент
знает) и событие
(ни одного билета студент не знает)
противоположное.
Поэтому
P(A)+P(
)=1
или
P(A)=1P(
)
P(
)=C
C
=24/91,
P(A)=124/91=
.
Решение 2. Требование, хотя бы один билет попадется студенту, на который он может ответить будет осуществлено, если произойдет любое из следующих трех несовместных событий: B студент знает один билет, С 2 билета, D 3 билета. Интересующее нас событие A можно представить в виде суммы событий A=B+C+D. По теореме сложения вероятностей P(A)=P(B)+P(C)+P(D)
P(B)=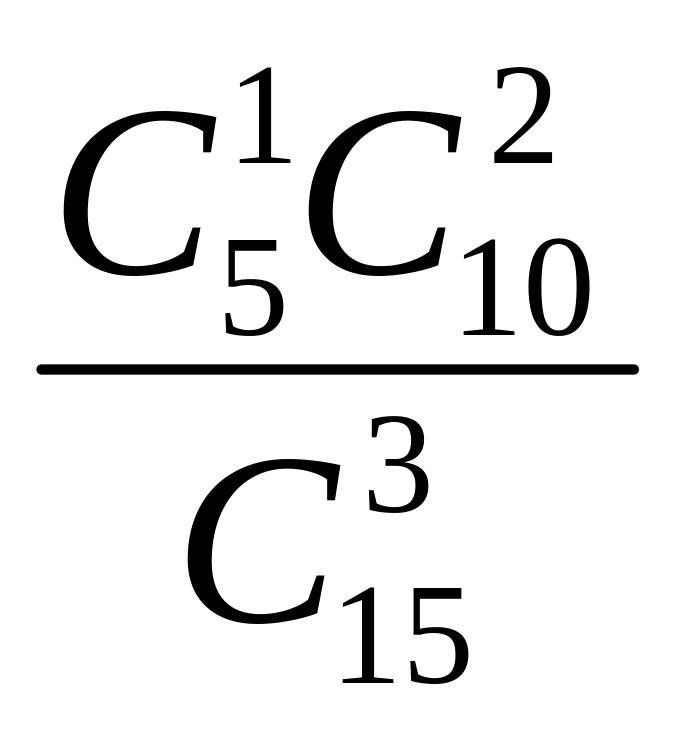
=
;P(C)=
=
;
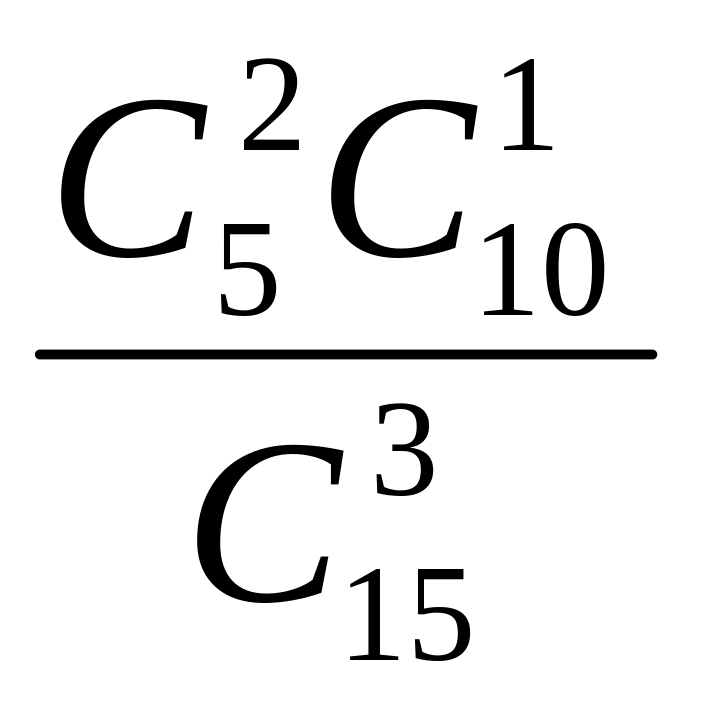P(D)=
=
P(A)=
+
+
=
.
Теорема 2. (обобщенная теорема сложения). Если событие С представимо в виде суммы двух событий А и В, где A и В -- любые события из одного поля, то
Р(С)=Р(А+В)=Р(А) + Р(В) - Р(АВ). (3.4)
Используем диаграмму Венна для иллюстрации этой теоремы (рис. 5).
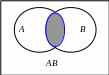
Рис. 5
Пример3.3. Прогноз метеорологов:
Р(дождь)=0,4; Р(ветер)=0,7; Р(дождь и ветер)=0,2. Какова вероятность того, что будет дождь или ветер?
Решение. По формуле сложения вероятностей (1.5):
Р(дождь или ветер) = Р(дождь) + Р(ветер) - Р(дождь и ветер)=0,4+0,7-0,2=0,9.
Пример 3.4. Определить вероятность того, что наудачу выбранное целое положительное число делится на 2 или на 3.
Решение. Введем следующие обозначения событий:
А={число делится на 2}, В={число делится на 3}, С={число делится на 2 или 3}. Тогда С=А+В, где А и В совместные события, так как имеются целые положительные числа, которые делятся и на 2, и на 3. Используя формулу (1.5), получим
Р(С)=Р(А+В)=Р(А)+Р(В) - Р(АВ)=1/2+1/3-1/6=2/3.
Для вероятности суммы трех событий А, В, С справедлива формула
Р(А+В+С)=Р(А)+Р(В)+Р(С)-Р(АВ)-Р(АС)-Р(ВС)+Р(АВС).
Методом математической индукции можно показать, что для n слагаемых событий имеет место следующее равенство
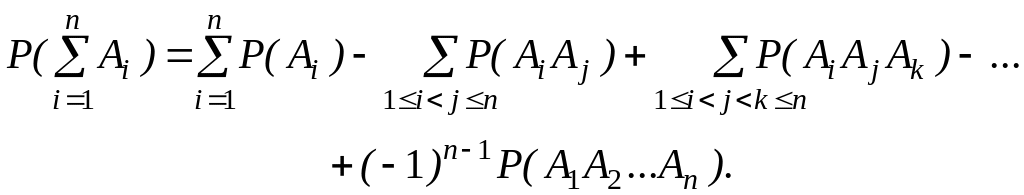(3.5)
Формула (3.5) есть общее выражение теоремы сложения вероятностей.