
Термодинамические основы комбинированной выработки энергии. Китаев Д.Н., Мартыненко Г.Н
.pdf
Д. Н. Китаев, Г. Н. Мартыненко
ТЕРМОДИНАМИЧЕСКИЕ ОСНОВЫ КОМБИНИРОВАННОЙ ВЫРАБОТКИ ЭНЕРГИИ
Учебное пособие
Воронеж 2021
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
Д. Н. Китаев, Г. Н. Мартыненко
ТЕРМОДИНАМИЧЕСКИЕ ОСНОВЫ КОМБИНИРОВАННОЙ ВЫРАБОТКИ ЭНЕРГИИ
Учебное пособие
Воронеж 2021
УДК 621.1(075.8) ББК 31.361я7
К45
Рецензенты:
кафедра теплогазоводоснабжения Юго-Западного государственного университета, г. Курск (д-р техн. наук, проф. В. С. Ежов);
АО «Гипрониигаз» (генеральный директор, председатель НТС, д-р техн. наук, проф. А. Л. Шурайц)
Китаев, Д. Н.
Термодинамические основы комбинированной выработки энергии: учебное пособие / Д. Н. Китаев, Г. Н. Мартыненко; ФГБОУ ВО К45 «Воронежский государственный технический университет». – Воронеж:
Изд-во ВГТУ, 2021. – 71 с.
ISBN 978-5-7731-0978-5
В учебном пособии изложен теоретический материал процессов истечения и дросселирования. Представлены методики расчета параметров водяного пара и изменения состояния в процессе комбинированной выработки энергии и основы технико-экономического анализа. Рассмотрено построение процессов изменения состояния пара в i-S и T-S диаграммах при дросселировании и истечении. Представлены примеры расчетов.
Издание предназначено для студентов, обучающихся по направлению 13.04.01 «Теплоэнергетика и теплотехника» (программа магистерской подготовки «Теплоэнергетика и теплотехника»), дисциплине «Комбинированная выработка энергии», всех форм обучения.
Ил. 17. Табл. 11. Библиогр.: 9 назв.
УДК 621.1(075.8) ББК 31.361я7
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета
ISBN 978-5-7731-0978-5 |
© Китаев Д. Н., Мартыненко Г. Н., 2021 |
|
© ФГБОУ ВО «Воронежский |
|
государственный технический |
|
университет», 2021 |
ВВЕДЕНИЕ
Всоответствии с учебным планом студенты магистратуры, обучающиеся по направлению 13.04.01 «Теплоэнергетика и теплотехника» (программа магистерской подготовки «Теплоэнергетика и теплотехника») изучают дисциплину «Комбинированная выработка энергии» на дневном отделении в третьем семестре, а заочном – в четвертом. Дисциплина предусматривает лекционные и практические занятия.
Впредставленном пособии рассмотрен теоретический материал по процессам истечения и дросселирования, находящим широкое применение при производстве электрической и тепловой энергии. Подробно описаны свойства водяного пара, представлены формулы для расчета при различных состояниях.
Рассмотрены методики построения процессов изменения состояния водяного пара в контурах паротурбинной установки с одним регулируемым отбором
вi-S и Т-S- диаграммах. Рассмотрена упрощенная методика расчета термодинамических и технико-экономических параметров комбинированной выработки энергии.
Значительная часть пособия посвящена рассмотрению практических примеров, связанных с процессами, происходящими с водяным паром при комбинированной выработке. Представлен пример расчета характеристик конденсационной турбины и построения режимов ее работы.
Вконце каждого практического примера есть задания для самостоятельного закрепления материала по вариантам. В процессе выполнения практических заданий происходит закрепление и углубление полученных студентом теоретических знаний. Справочные данные по свойствам водяного пара, представленные в приложениях, позволяют обойтись без использования другой литературы.
Приведенные иллюстрации процессов изменения состояния водяного пара в i-S диаграмме позволяют студентам заочного обучения самостоятельно освоить материал и научиться пользоваться справочными данными.
Приступая к изучению курса «Комбинированная выработка энергии», студент должен обладать знаниями по технической термодинамике. В настоящее время поступать в магистратуру направления 13.04.01 «Теплоэнергетика и теплотехника» имеют право студенты, закончившие бакалавриат любых направлений, даже не технических. В ряде специальностей курс технической термодинамики не изучается. Одной из целей пособия является восполнить знания
вразделах крайне необходимых для успешного освоения дисциплины «Комбинированная выработка энергии» и понимания сущности физических процессов, проходящих в контурах подобных установок.
Пособие может быть рекомендовано для студентов магистратуры других направлений, изучающих термодинамическские основы процессов комбинированной выработки энергии, а также студентам бакалавриата для углубленного изучения. Пособие может быть также полезно в инженерной практике.
Все приведенные в пособии иллюстрации являются авторскими.
3

1. ИСТЕЧЕНИЕ
1.1.Скорость истечения
Рассмотрим резервуар неограниченной емкости (р1=const) в котором установлен насадок (сопло). Сопло – это канал в котором происходит увеличение скорости потока w. Если давление р2<р1 (рис. 1.1), то газ будет вытекать в окружающую среду. Такой процесс называется истечение. Истечение газа является основным процессом в газовых и паровых турбинах.
р1,υ1,t1 |
р2 |
|
|
|
ру |
Рис. 1.1. Схема процесса истечения
Скорость истечения – скорость, установившаяся в устье сопла, т.е. на выходе из него.
По назначению сопла разделяются на сходящиеся, расходящиеся и цилиндрические.
Рассмотрим установившееся истечение (скорости в любом сечении сопла постоянные) газа из резервуара неограниченной емкости через суживающиеся сопло при условии р2=ру (полное расширение). Ввиду больших скоростей истечения и малого времени прохождения газа через сопло, процесс будем считать адиабатным dq=0.
Из первого закона термодинамики для потока, в адиабатном процессе при условии отсутствия технической работы, трения и работы силы тяжести (dlтех=dlтрения=gdh=0), получим выражение энтальпии газа i:
di = − |
1 dw2 . |
(1.1) |
||
|
2 |
|
|
|
Интегрируя уравнение (1.1) при условии w1=0, получим выражение для |
||||
скорости истечения |
|
|
|
|
w2 = |
|
|
. |
(1.2) |
|
2(i1 − i2 ) |
|||
Уравнение (1.2) носит универсальный характер и справедливо как для идеальных, так и для реальных газов. Рассмотрим изменение энтальпии идеального газа, при условии постоянной теплоемкости. Тогда можно записать:
4
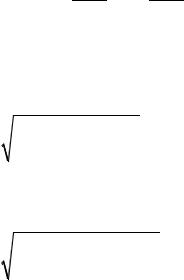
i1 − i2 = cp (T1 − T2 ).
С учетом уравнения Майера cp − cυ = R , можно записать:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ cυ |
|
|
|
cυ |
|
|
|
1 |
|
|
||
c |
p |
= R + c |
= R |
= R 1+ |
|
|
|
= R 1+ |
|
|
|
= |
|||||
|
|
|
|
|
|
|
|
||||||||||
|
υ |
|
|
|
|
c |
|
− c |
|
|
cp |
|
|
|
|
||
|
|
|
|
|
R |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
p |
υ |
|
|
|
−1 |
|
|||
|
|
|
|
|
|
|
cυ |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
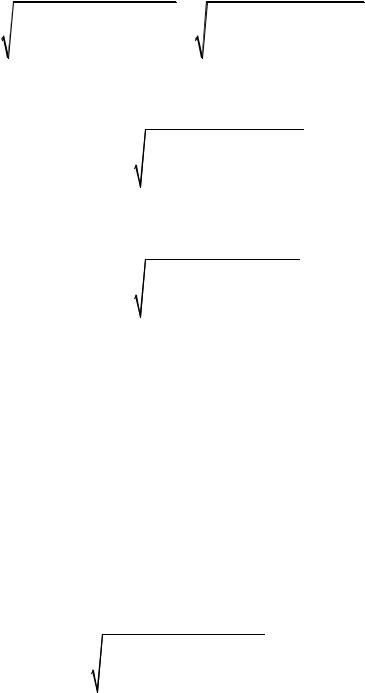
=R 1+ k 1−1 = R k k−1.
(1.3)
(1.4)
Подставляя выражения (1.3), (1.4) в уравнение скорости (1.2), получим
|
|
|
|
|
|
||
w = |
2 |
k |
R (T − T ) , |
(1.5) |
|||
|
|||||||
2 |
|
k −1 |
1 |
2 |
|
|
|
|
|
|
|
|
|
||
или с учетом уравнения Клапейрона pυ = RT :
|
|
|
|
|
|
|
|
|
w = |
2 |
k |
|
( p υ − p υ |
|
) . |
(1.6) |
|
k −1 |
|
|||||||
2 |
|
1 1 2 |
2 |
|
|
|
||
Уравнения (1.4) и (1.5) являются интерпретацией уравнения (1.2) и справедливы только для идеальных газов.
Вспомним уравнение адиабатного процесса, необходимое для дальнейших выводов:
pυk = const , или p υ k = p υ k . |
(1.7) |
|||
1 |
1 |
2 |
2 |
|
Выражая из уравнения Клапейрона удельный объем υ = RTp , подставляя его в уравнение (1.7) получим:
|
RT1 |
k |
|
|
|
RT2 |
k |
|||
p1 |
|
= p2 |
|
, |
||||||
|
p1 |
|
|
|
|
|
p2 |
|
|
|
|
|
k |
p1 |
k |
|
|
|
|
||
T2 |
|
|
= |
p1 |
, |
|
||||
p2 |
p2 |
|
||||||||
|
T1 |
|
|
|
|
|
|
|
||
5
|
|
|
1−k |
|
|
|
k−1 |
k−1 |
|
|
T2 |
|
p1 |
k |
|
p2 |
|
k |
|
||
= β k . |
(1.8) |
|||||||||
= |
|
= |
|
|
||||||
p2 |
p1 |
|
||||||||
T1 |
|
|
|
|
|
|
|
Преобразуем уравнение (1.6) к виду:
w = 2 |
k |
|
p υ |
1 |
− |
p2υ2 |
|
= |
|
2 |
|
k |
p υ |
1 |
− |
RT2 |
. |
(1.9) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
k −1 |
1 1 |
|
|
|
|
|
|
|
|
|
k −1 |
1 1 |
|
|
|
|
|
||||||
|
|
|
|
p1υ1 |
|
|
|
|
|
|
RT1 |
|
||||||||||||
Подставляя выражение (1.6) в (1.7) получим |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
k−1 |
|
|
|
|
||||
|
|
|
|
w2 |
= |
2 |
|
|
|
|
p1υ1 1− β k |
|
, |
|
|
(1.10) |
||||||||
|
|
|
|
k −1 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
или с учетом уравнения Клапейрона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
w2 |
|
|
|
|
|
k |
|
|
RT1 |
|
k−1 |
|
|
|
|
|
||||
|
|
|
|
= |
2 |
|
|
|
|
1− |
β k |
. |
|
|
(1.11) |
|||||||||
|
|
|
|
|
k −1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, уравнения (1.10) и (1.11) определяют скорость истечения идеального газа.
1.2. Расход истечения. Критическая скорость
Секундным массовым расходом (М), кг/с называется масса рабочего тела m, протекающего в секунду через данное сечение канала площадью F:
M= ρ2 = F w2 .
υ2
Подставим уравнение (1.10) в (1.12):
M = F 2 |
k |
|
p1υ1 |
|
k−1 |
|
|
1− β k |
. |
||||
|
|
2 |
||||
|
k −1 υ2 |
|
|
|
||
Из выражения (1.7) получим
(1.12)
(1.13)
6
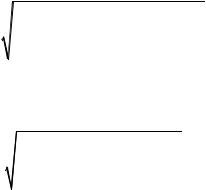
|
|
|
|
|
|
1 |
|
|
|
|
−1 |
|
|
|
|||
|
|
|
|
|
|
p1 |
|
k |
|
|
|
|
|
|
|
||
|
υ |
|
= |
|
υ |
= β k υ , |
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|||
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|||
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тогда υ2 |
= β k υ2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим (1.14) в (1.13) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M = F |
|
2 |
|
k |
|
|
p1υ1 |
|
|
2 |
k−1+ |
2 |
|
, |
||
|
|
|
|
|
|
β k − β k k |
|
||||||||||
|
|
|
|
|
|
|
2 |
||||||||||
|
|
|
|
k −1 υ |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||
и после преобразований получим
M = F 2 |
k |
|
p1 |
|
2 |
k+1 |
|
|
|
|
β k − β k |
. |
|||||
k −1υ1 |
||||||||
|
|
|
|
|
||||
(1.14)
(1.15)
Из выражения (1.15) следует, что при известных начальных параметрах рабочего тела р1, υ1 и площади сопла F, расход М зависит только от отношения
давлений β, т.е M = f (β ).
Определим максимальный расход (найдем производную, приравняем к нулю и выразим β):
|
∂M |
= |
2 |
2 |
−1 |
− |
k +1 |
k−1−1 |
= |
0, β |
2−k |
k +1 |
1 |
2−k |
− |
1 |
k +1 |
, |
||||||||
|
∂β |
|
k |
β k |
|
k |
β k |
|
k = |
|
|
2 |
|
β k |
, β k |
|
k = |
2 |
||||||||
|
F ,υ ,р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
k |
+1 |
k |
|
2 |
|
|
|
k |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
k−1 |
|
|
|
k−1 |
. |
|
|
|
|
(1.16) |
|||||||
|
|
|
|
|
|
|
|
β = |
2 |
|
|
= |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k +1 |
|
|
|
|
|
|
|
|
|||||
При значении β, определяемом уравнением (1.16) будет наблюдаться максимальный расход.
На рис. 1.2 представлен обобщенный график, построенный по уравнению
(1.15).
Уравнение (1.15) дает два нулевых расхода: при β=0 и β=1, а при некотором значении β наблюдается максимум. Давление в выходном сечении суживающихся сопел, при котором наблюдается максимальный расход, называется критическим давлением (рк). Это минимальное давление, которое может установиться в выходном сечении суживающихся сопел.
7

М 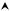
0 |
βк |
1 β |
Рис. 1.2. Зависимость расхода от соотношения давлений
Из рис. 1.2 следует, что расход увеличивается при понижении давления среды р2 до достижения давления рк (правая кривая). Дальнейшее понижение р2 приводит к снижению значения расхода М, и при достижении абсолютного вакуума истечение прекращается (пунктирная линия)? Подобный вывод противоречит логике и экспериментальным данным. Ошибка заключается в том, что при выводе уравнения (1.15) было принято условие полного расширения газа р2=ру, но опыты доказали что это неверно. После достижения давления рк расход постоянен и не изменяется при понижении давления р2 (прямая горизон-
тальная линия на рис. 1.2). Отношение |
рк |
= βк называют критическим отно- |
|
р1 |
|||
|
|
шением давлений и определяют его по формуле (1.16). Из выражения (1.16) следует, что βк зависит от показателя адиабаты k, т.е. от рода газа. Подставляя в уравнение (1.16) константу k, получим значения βк. Подставляя полученное значение βк в уравнение (1.15), получим выражение для определения расхода М (таблица) для различных газов.
Таблица
Значения βк ,М, wк
газы |
k |
βк |
М |
|
|
|
|
|
wк |
|
|
|
|
1,7 |
0,482 |
|
|
|
|
|
|
|
|
|
|
одноатомные |
0,731F |
|
p1 |
|
|
|
1,122 |
|
|
|
||
|
|
|
|
|
|
p1υ1 |
|
|
||||
|
|
υ1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
1,41 |
0,528 |
|
|
|
|
|
|
|
|
|
|
двухатомные |
0,686F |
|
p1 |
|
|
|
1,082 |
|
|
|
||
|
|
|
|
|
|
p1υ1 |
|
|||||
|
|
υ1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
1,3 |
0,546 |
|
|
|
|
|
|
|
|
|
|
трехатомные, |
0,667F |
|
p1 |
|
|
|
|
|
|
|
||
|
|
|
|
1,063 |
p1υ1 |
|||||||
перегретый пар |
|
|
|
|
|
|
||||||
|
|
υ1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
1,135 |
0,577 |
|
|
|
|
|
|
|
|
|
|
сухой насыщенный |
0,636F |
|
p1 |
|
|
|
|
|
|
|
||
|
|
|
|
1,031 |
p1υ1 |
|||||||
пар |
|
|
|
|
|
|
||||||
|
|
υ1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
8

Из таблицы следует, что для многих газов βк ≈0,5.
В суживающихся соплах давление не может быть ниже критического рк, следовательно, скорость не может быть больше некоторого значения wк (критическая скорость).
Подставляя выражение (1.16) в ( 1.11) найдем выражение критической скорости
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
k−1 |
|
|
|
|
|
|
||
|
|
k |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
k |
k −1 RT |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
k−1 k |
|
|
||||||||||||||
w |
= 2 |
RT |
1− |
|
|
= |
2 |
, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
к |
|
k −1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
k −1 k +1 |
1 |
|||||||||||
|
|
|
|
|
|
k +1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
w |
= |
|
2 |
|
k |
|
RT , |
|
|
|
|
|
|
|
(1.17) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
к |
|
|
|
|
k +1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
или w |
|
|
= |
|
2 |
|
|
k |
|
|
р υ . |
|
|
|
|
|
(1.18) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
к |
|
|
|
|
|
|
|
k +1 1 |
1 |
|
|
|
|
|
|
|
|||||||
В таблице представлены выражения для wк с учетом значений k.
Проходя через сопло, параметры газа изменяются от начальных р1,υ1 до состояния в выходном сечении рк, υк по закону адиабатного процесса
p1υ1k = pкυкk . Выражаем υ1 и р1:
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
pк |
|
k |
|
|
|
|
; |
|
|
|||
|
υ |
= |
|
υ |
|
= β |
kυ |
|
|
|
|||||||
|
|
|
|
|
|
к |
к |
|
|
||||||||
|
|
1 |
|
|
|
p1 |
|
|
|
|
k |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
= |
p υ k |
|
= |
|
|
|
p |
υ k |
= β |
−1 |
p |
. |
||||
|
к к |
|
|
|
к к |
k |
|||||||||||
1 |
|
υ1k |
|
|
|
|
|
|
1 |
k |
|
|
к |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
βkkυk |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляем полученные выражения для υ1 и р1 в уравнение (1.18):
w = |
|
k |
|
β −1 |
р |
1 |
|
|
|
k |
р υ |
|
1−k |
|
2 |
β kυ |
|
= |
2 |
β |
k . |
||||||||
k +1 |
|
|
||||||||||||
к |
|
k |
k k |
k |
|
|
k +1 k k |
|
k |
|||||
9
