Учебное пособие 1816

Примеры линейных пространств

1. R1 – множество всех векторов, лежащих на одной прямой l , с обычными операциями сложения векторов и умножения вектора на число (рис. 1).

l

a

b

Рис. 1. Множество векторов, лежащих на одной прямой

2. R2 – множество всех векторов, лежащих в одной плоскости, с введенными обычными операциями сложения векторов и умножения вектора на число (рис. 2).

a

b

Рис. 2. Множество векторов, лежащих в одной плоскости

3.R3 – множество всех векторов, лежащих в пространстве, с обычными операциями сложения векторов и умножения вектора на число.

4.Множество всех матриц {Am×n } размера m ×n с обычными операциями сложения матриц и умножения на число.

5.Множество всех многочленов {Pn (x)} степени не выше n с обычными операциями сложения многочленов и умножения на число.

Отметим, что множество всех многочленов степени n не будет образовывать линейного пространства, так как при сложении двух многочленов

41

может получиться многочлен, степень которого может оказаться меньше n .

6.Множество C[a,b] ={y = y(x)} всех непрерывных на отрезке [a, b] функций.

7.Множество упорядоченных наборов из n чисел

Rn ={(x1, x2 ,..., xn )}, где x1, x2 ,..., xn – некоторые числа,

с операциями сложения и умножения на число, вводящимися так же, как и для матриц, т.е. соответствующие компоненты складываются и умножаются на число. Такое пространство будем называть n -мерным координатным пространством.

8. Приведем пример множества, не являющегося линейным пространством. Множество его элементов определим как наборы из n чисел, как и в предыдущем примере, причем операция сложения будет определяться по такому же правилу, как и в примере 7 – сложение соответствующих компонентов, а операция умножения на число по другому правилу, а именно

α x = (αx1, x2 ,..., xn ).

Проверим, выполнена ли в таком случае аксиома 7. С одной стороны,

(α + β) x = ((α + β)x1, x2 ,..., xn ).

А с другой

α x + β x = ((α + β)x1,2x2 ,...,2xn ).

Очевидно, что (α + β) x ≠α x + β x . Следовательно, указанное множество не образует линейного пространства.

4.2. Линейная зависимость и независимость векторов

Определение. Векторы x1, x2 ,..., xk линейного пространства R называются линейно зависимыми, если существуют такие числа α1,α2 ,...,αk , не равные одновременно нулю, что

42

Векторы, не являющиеся линейно зависимыми, называются линейно не-

зависимыми.

Другими словами, для линейно независимых векторов равенство (4.1) выполняется тогда и только тогда, когда α1 =α2 = ... =αk = 0.

Пусть векторы x1, x2 ,..., xk R линейно зависимы, тогда существуют такие числа α1,α2 ,...,αk , хоты бы одно из которых отлично от нуля, что выполнено равенство (4.1). Для определенности будем считать, что αk ≠ 0 . Тогда (4.1) можно записать в виде

x1, x2 ,..., xk линейно зависимы, то, по крайней мере, один из них линейно вы-

ражается через остальные. Ясно, что верно и обратное, т.е. что если одни из векторов линейно выражается через остальные, то все эти векторы в совокупности линейно зависимы.

Рассмотрим примеры линейно зависимых и независимых векторов.

Пример 1. Множество R1 всех векторов, лежащих на одной прямой. В этом линейном пространстве любые два вектора линейно зависимы. Действительно, пусть a и b – два вектора, лежащие на одной прямой, тогда найдется такое число λ , не равное нулю, что a = λb . Т.е. вектор a линейно выражается через вектор b и эти два вектора линейно зависимы.

Пример 2. Множество R2 всех векторов, лежащих в одной плоскости. В этом линейном пространстве любые два неколлинеарных вектора линейно независимы ([3, §4, c. 31]), а любые три вектора линейно зависимы, так как любой вектор плоскости может быть разложен по двум неколлинеарным векторам.

43

Пример 3. Множество R3 всех векторов, лежащих в трехмерном пространстве. В этом линейном пространстве любые три некомпланарных вектора линейно независимы, а любые четыре вектора линейно зависимы ([1, гл. 1, §2, c. 65]).

4.3. Размерность и базис линейного пространства

Определение. Линейное пространство R называется n -мерным, если в нем можно найти n линейно независимых векторов, а любые (n +1) векторы линейно зависимы.

Таким образом, размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Размерность пространства обозначается dim(R) .

Линейное пространство размерности n называется n -мерным линей-

ным пространством и обозначается Rn .

Из рассмотренных ранее примеров следует, что dim(R1 ) =1, dim(R2 ) = 2 , dim(R3 ) = 3.

Пространство, имеющее конечную размерность, называется конечномерным. Если в пространстве можно указать сколь угодно много линейно независимых векторов, то оно называется бесконечномерным. Например, пространство C[a,b] непрерывных на отрезке [a, b] функций является бесконеч-

номерным.

Определение. Базисом n -мерного линейного пространства Rn называется любая упорядоченная система n линейно независимых векторов.

Теорема. Любой вектор x линейного n -мерного пространства Rn можно всегда представить, и притом единственным образом, в виде линейной комбинации векторов базиса.

Доказательство. Пусть x – произвольный вектор n -мерного пространства, а e1, e2 ,..., en – базис в Rn . Так как любая система (n +1) векторов является линейно зависимой, то существует набор чисел α1,α2 ,...,αn ,α , не всех равных нулю, таких, что выполняется равенство

α1e1 +α2e2 +... +αnen +αx =θ .

44

Очевидно, что именно α ≠ 0 , так как если α = 0 , то в силу линейной независимости векторов e1, e2 ,..., en все αi = 0 , что противоречит условию линейной зависимости. Значит, можно последнее равенство записать так

x = −αα1 e1 − αα2 e2 −... − ααn en .

Обозначим xi = −ααi , i =1,2,..., n . Окончательно получим

Таким образом, получено разложение произвольного вектора x по векторам базиса e1, e2 ,..., en .

Покажем, что в заданном базисе разложение (4.3) будет единственным. Действительно, пусть существует помимо (4.3) еще одно разложение

x = y1e1 + y2e2 +... + ynen ,

тогда, вычитая из уравнения (4.3) второе уравнение, получим

θ = (x1 − y1 )e1 + (x2 − y2 )e2 +... + (xn − yn )en .

Так как векторы e1, e2 ,..., en образуют базис, то последнее условие будет выполняться тогда и только тогда, когда

x1 = y1, x2 = y2 ,..., xn = yn ,

что и доказывает единственность разложения по векторам базиса.

Числа xi , i =1,2,...,n , называются координатами вектора x в базисе e1, e2 ,..., en . Вследствие теоремы о разложении в данном базисе вектор x может быть задан набором чисел (координат)

x = (x1, x2 ,..., xn ).

Отметим, что между вектором и его координатами (в некотором базисе) устанавливается взаимнооднозначное соответствие.

45

Замечание. Координаты вектора x могут быть записаны как строкой

x1

x = (x1, x2 ,..., xn ), так и столбцом x = xM2 , который будем называть коорди-

xn

натным столбцом. Кроме того, можно показать, что векторы линейно зависимы тогда и только тогда, когда линейно зависимы их координатные столбцы. (Доказательство см., например, [2, гл. 6, §1, c. 193]).

4.4. Действия над векторами

Пусть x = x1e1 + x2e2 +... + xnen и y = y1e1 + y2e2 +... + ynen – векторы n - мерного линейного пространства Rn , разложенные по одному базису.

1. Сложение векторов

x + y = (x1 + y1 )e1 + (x2 + y2 )e2 +... + (xn + yn )en = (x1 + y1, x2 + y2 ,..., xn + yn )

Итак, при сложении векторов их координаты складываются.

2. Умножение вектора на число

λx = λx1e1 + λx2e2 +... + λxnen = (λx1, λx2 ,...,λxn ).

При умножении вектор на число координаты вектора умножаются на это число.

3. Разность векторов

x − y = x +(−1) y = (x1 − y1 )e1 +(x2 − y2 )e2 +... +(xn − yn )en = = (x1 − y1, x2 − y2 ,..., xn − yn )

Итак, при вычитании векторов их координаты вычитаются.

Пример 1. Рассмотрим пятимерное пространство R5 , в котором базисом является набор векторов e1, e2 , e3, e4 , e5 . Найдем координаты векторов e2 и x = 3e1 − e3 + 2e4 в указанном базисе.

Разложение вектора e2 по базису имеет вид

46

e2 = 0 e1 +1 e2 +0 e3 +0 e4 +0 e5 ,

отсюда координаты вектора e2 будут (0,1,0,0,0). Разложение вектора x по базису имеет вид

x = 3 e1 +0 e2 −1 e3 + 2 e4 +0 e5 ,

следовательно, координаты вектора x будут (3,0,−1,2,0).

Пример 2. Даны координаты векторов x и y в некотором базисе x = (2,−1,3,5), y = (−1,4,0,−2). Найти координаты вектора 2x −3y .

Используя правила умножения вектора на число и вычитания векторов, получаем

2x −3y = 2(2,−1,3,5)−3(−1,4,0,−2)= (7,−14,6,16).

Пример 3. Даны векторы a = e1 + e2 + e3 , b = 2e2 + 3e3 , c = e2 +5e3 , где e1 , e2 , e3 – базис линейного пространства R .

1.Доказать, что векторы a , b и c образуют базис.

2.Найти координаты вектора d = 2e1 − e2 + e3 в базисе a , b , c . Отметим, что размерность пространства R равна трем, так как именно

три вектора e1 , e2 , e3 образуют базис. Следовательно, для того чтобы векторы a , b , c образовывали базис, достаточно, чтобы они были линейно независимыми. Проверим это.

Составим линейную комбинацию векторов a , b , c :

α1a +α2b +α3c =θ .

Запишем полученное выражение в координатной форме в базисе e1 , e2 ,

Полученная система, является однородной.

Как известно, однородная система имеет единственное решение, при-

47

чем нулевое, тогда и только тогда, когда ее определитель не равен нулю. Вычислим определитель нашей системы:

вестно, любой вектор единственным образом раскладывается по векторам базиса, т.е.

d = x1a + x2b + x3c .

Запишем полученное выражение в координатной форме в базисе e1 , e2 ,

e3 :

и перейдем к системе

Найдем решение этой системы, подставив x1 = 2 во второе и третье уравнения системы:

2x2 + x3 = −3,3x2 +5x3 = −1.

Отсюда x2 = −2, x3 =1. Следовательно, координаты вектора d в базисе a , b , c будут (2,−2,1) и разложение примет вид d = 2a −2b + c .

48

4.5. Переход к новому базису

В линейном пространстве базис определяется неоднозначно. Пусть {e1, e2 ,..., en }– некоторый базис в n -мерном пространстве, будем называть его старым базисом, а {e1', e2 ',..., en '} – другой (новый) базис. Разложим векторы нового базиса по векторам старого базиса:

Матрица P называется матрицей перехода от старого базиса к новому.

Столбцы матрицы – это координатные столбцы векторов e1', e2 ',..., en ' в базисе e1, e2 ,..., en . Так как векторы e1', e2 ',..., en ' линейно независимы, то столбцы матрицы P будут также линейно независимыми. Следовательно, определитель матрицы P не равен нулю (det P ≠ 0 ) и матрица является невырожденной.

Можно показать, что любая невырожденная матрица может служить матрицей перехода к новому базису. [2, гл.6, §1, с.196]

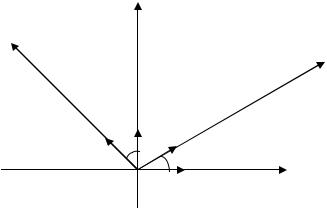
Пример. Пусть i , j – единичные векторы, направленные по осям прямоугольной декартовой системы координат. Повернем оси координат на угол α против часовой стрелки, и пусть i ', j' – новые базисные векторы (рис.3).

Разложим векторы нового базиса по векторам старого базиса, получим

i ' = cosα i +sinα j,j' = −sinα i + cosα j.

49