
Учебное пособие 1631
.pdf
Правила дифференцирования
1. y Cu(x) ,
2. y u(x) v(x) , 3. y u(x)v(x) ,
4. y u( x) , v( x)
y' Cu (x) .
y u (x) v (x) .
y u (x)v(x) u(x)v (x) .
y' u (x)v(x) u(x)v (x) . v2 (x)
5. Производная сложной функции y f (u), u (x).
y f (u) (x) .
u x
6. Производная параметрически заданной функции
y f (t) |
|
|
|
|
|
x (t) , |
y |
|
yt |
. |
|
|
|
||||
|
x |
|
xt |
|
|
|
|
|
|
||
7. Производная обратной функции x |
1/ y . |
||||
|
|
|
|
y |
x |
Пример 3.14. Найти производную функции y cos x . x2
Решение. Воспользуемся правилом дифференцирования дроби
y |
x2 (cosx) cosx (x2 ) |
|
x 2 (sin x) 2x cos x |
|
x(sin x) 2 cos x |
. |
|||
x4 |
|
|
x 4 |
x3 |
|
||||
|
|
|
|
|
|
|
|||
|
Пример |
3.15. Найти |
производную сложной |
функции |
|||||
y ln6 (4x7 9). |
|
|
|
|
|
|
|
||
|
Решение. |
Обозначим |
ln(4x7 9) u. |
Тогда |
y u6 . |
||||
По правилу дифференцирования сложной функции имеем |
|
||||||||
|
|
|
|
|
40 |
|
|
|
|

|
|
|
|
|
|
|
1 |
|
|
|
|
y (u 6 ) |
(ln(4x7 |
9)) |
6 ln5 (4x7 |
9) |
|
|
(4x7 |
9) |
|
||
|
|
||||||||||
u |
|
|
|
x |
|
|
4x7 |
|
|
x |
|
|
|
|
|
|
|
|
9 |
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
|
6 ln5 (4x7 |
9) |
|
|
28x6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x7 9 |
|
|
|
|
|
|
|
||
Пример 3.16. Найти производную сложной функции y ln3 cos 6 2x 1 .
2x 1 .
Решение:
Пример 3.17. Найти производную функции arcsin x 8x .
Решение. Основание и показатель степени заданной функции зависят от х. Поскольку в таблице производных нет степенно-показательных функций, прологарифмируем
y arcsin x 8x , чтобы затем найти ее производную
ln y ln arcsin x 8x 8x ln arcsin x.
Продифференцируем по х обе части полученного
равенства. |
Функция |
|
lnу |
|
|
есть |
сложная |
функция от |
х |
|
и |
|||||||||||||||
(ln y) |
1 |
y . Тогда |
1 |
y 8ln arcsin x 8x |
1 |
|
|
. Отсюда |
|
|
|
|
||||||||||||||
y |
y |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
y y |
|
|
|
|
|
|
|
|
|
|
|
8x |
|
|
|
|
|
|
|
|
|
|
||||
|
8ln arcsin x 8x |
|
|
|
|
|
|
(arcsin) |
|
8ln arcsin x 8x |
|
|
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
1 x |
2 |
|
|
|
|
|
1 |
x |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Использованный метод называют логарифмическим дифференцированием.
41
Пример 3.18. Найти |
производную |
y |
параметрически |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
x 7(t 2 |
ln t), |
|
|
|
|
||
заданной функции |
|
|
|
|
|
|
||||||
|
|
|
|
|
y 2(8 sin 3t). |
|
|
|
||||
Решение. |
Вычислим |
производные |
yt 6cos 3t , |
|||||||||
|
1 |
|
7 2t 2 |
1 |
. Получаем |
y'x |
6t cos 3t |
. |
||||
xt 7 2t |
|
|
|
|
|
|
7 2t 2 1 |
|||||
|
t |
|
|
|||||||||
|
t |
|
|
|
|
|
|
|
||||
Пример 3.19. Найти |
производную |
y |
, если функция |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
задана уравнением F(x, y) = 0, не разрешенным относительно y — неявно заданная функция y3 3y 2x 0.
Решение. Продифференцируем обе части заданного
равенства по х, считая, |
что |
у есть |
функция от |
х. |
Тогда |
||||
3y 2 y 3y 2 0; |
3y ( y 2 |
1) 2 , откуда |
y |
|
2 |
|
. |
||
|
|
||||||||
|
|
||||||||
|
|
|
|
|
x |
|
3(1 y2 ) |
|
|
|
|
|
|
|
|
|
|
||
Производная |
y f x |
является |
функцией |
от |
x и |
||||
называется производной первого порядка.
Если функция f x дифференцируема, то производная от
производной определена и называется производной второго порядка, обозначается
|
|
|
|
d 2 y |
|
d |
dy |
|||
y |
|
|
|
|
|
|
. |
|||
|
f x |
dx2 |
|
|
||||||
|
|
|
|
|
dx dx |
|||||
По аналогии, производной |
n -го |
порядка называется |
||||||||
производная от производной |
n 1 -го порядка, т. е. |
|||||||||
y n y n 1 .
Производные порядка выше второго называются производными высших порядков, причем порядок производной обозначается числом в скобках, записанным в виде верхнего индекса.
42

Пример 3.20. Найти производную 5-го порядка функции y ln x .
Решение. y ln x
|
|
2 |
|
|
6 |
|
|
|
|
||||
y |
4 |
|
|
|
|
, |
|
|
|||||
|
x3 |
|
|
x4 |
|
|
1x , y 5
|
1 |
|
|
1 |
|
y |
|
|
|
|
, |
|
x2 |
||||
x |
|
|
|
||
6 24 .x 4 5x
y 3 2 , x3
Введем понятие дифференциала функции. Пусть функция y f x дифференцируема на отрезке [a,b], т. е. приращение функции имеет вид y f x x ( x) , где (x) — величина бесконечно малая более высокого порядка по сравнению с x .
Главная линейная по x часть приращения функции y f x x называется дифференциалом функции и обозначается символом dy или df x . Дифференциал независимой перемен-
ной величины x совпадает с ее приращением x , т. е. dx x . Таким образом,
dy = y dx .
Задача нахождения дифференциала функции равносильна нахождению производной, так как, умножив последнюю на дифференциал аргумента, получим дифференциал функции. Большинство теорем и формул, относящихся к производным, сохраняют свою силу и для дифференциалов. Например:
1.d u x v x du x dv x .
2.d u x v x u x dv x v x du x .
|
|
u x |
|
u x dv x v x du x |
|
|
|||||
|
3. |
d |
|
|
|
|
|
|
|
. |
|
|
|
|
2 |
|
|
|
|||||
|
|
|
|
|
|
v |
x |
|
|
||
|
|
v x |
|
|
|
|
|||||
|
4. |
|
Дифференциал |
|
сложной |
функции |
обладает |
||||
инвариантностью |
формы, |
|
т. е., если |
y f u , |
u x , то |
||||||
dy |
f u du . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
43 |
|
|
|
Пусть функция y f x дифференцируема, а аргумент x является независимой переменной. Тогда ее дифференциал или
первый дифференциал |
dy y dx также является функцией |
x . |
Если дифференциал оказался дифференцируемой функцией |
x , |
|
то дифференциал от |
дифференциала функции y f |
x |
существует и называется вторым дифференциалом или
дифференциалом второго порядка:
d dy d 2 y d y dx y dx dx y dx dx y dx 2 y dx2 .
Дифференциал n -го порядка определяется как дифференциал от дифференциала n 1 -го порядка:
d n y d d n 1 y .
Данные формулы справедливы, если x является независимой переменной.
Пример 3.21. Найти d 2 y , если y x3 , а x является независимой переменной величиной.
Решение: y 3x2 , y 6x , d 2 y 6x dx2 .
При вычислении пределов для раскрытия в них неопределенностей может быть использовано правило Лопиталя.
Теорема |
Лопиталя. |
Пусть |
функции f x |
и x |
|||
непрерывны и |
дифференцируемы |
в окрестности |
точки x0 |
||||
и обращаются в нуль в этой точке, т. е. |
f x0 x0 0 , кроме |
||||||
того, x0 0 , тогда, если существует предел |
|
||||||
|
lim |
f ' (x) |
A , то |
lim |
f (x) |
A . |
|
|
x x0 |
' (x) |
|
x x0 |
(x) |
|
|
|
|
|
44 |
|
|
|
|
Если производные f x |
и x удовлетворяют |
тем же |
|
условиям, что и функции |
f x |
и x , теорему |
можно |
применить еще раз: |
lim |
|
f (x) |
lim |
|
f (x) |
lim |
|
f (x) |
и т. |
|||||||||||
|
|
|
(x) |
|
(x) |
||||||||||||||||
|
|
|
x x0 (x) |
x x0 |
|
x x0 |
|
|
|
||||||||||||
Теорема справедлива и в том случае, когда x . |
|||||||||||||||||||||
Пример 3.22. Найти предел lim |
ln 5x 7 |
. |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
|
x 3 |
|
|
|
|
|
|
|
|||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln 5x 7 |
|
|
|
|
ln 5x |
|
|
|
|
|
|
5 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
5x 7 |
|||||||||||||
lim |
|
lim |
7 |
lim |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
x |
x 3 |
|
|
|
x |
|
|
|
|
|
|
x 1 |
|||||||||
|
|
|
|
x 3 |
|||||||||||||||||
Пример 3.23. Найти предел |
lim |
|
4x2 sin 7x |
. |
|
|
|
|
|||||||||||||
|
|
x2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
||||
Решение:
д.
0 .
|
4x2 sin 7x |
|
0 |
|
8x 7 cos7x |
|
|
|
|
|
|
8x 7 |
|
|
|
|
|
8 |
|
|
|
||||||||||||
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
lim |
|
|
|
|
|
lim |
|
|
|
|
|
. |
|||||
x |
4 |
|
|
|
|
4x |
3 |
|
|
|
|
|
3 |
|
|
|
|
2 |
|||||||||||||||
x 0 |
|
|
|
|
0 |
x 0 |
|
|
|
|
|
|
x 0 4x |
|
|
x 0 12x |
|
|
|
||||||||||||||
Правило Лопиталя может быть использовано и для |
|||||||||||||||||||||||||||||||||
исследования неопределенностей вида 0 , , |
1 , |
0 , |
|||||||||||||||||||||||||||||||
00 , |
, |
для |
чего |
указанные |
|
виды |
|
|
неопределенностей |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
сводятся к неопределенностям |
|
|
|
|
или |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 3.24. Найти предел lim sin 3x x . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: lim sin 3x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln(sin 3x) |
|
|
|
(ln(sin 3x)) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
lim |
eln(sin 3x) |
x |
lim ex ln(sin 3x) lim |
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
e |
|
|
|
x |
|
|
e |
x |
|
|
|
|||||||||||||||||||||
x 0 |
|
|
|
|
x 0 |
|
|
|
x 0 |
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
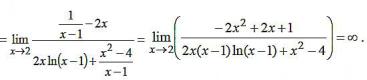
3 cos3x |
||||
|
|
|
|
|
sin3x |
||||
|
||||
|
|
1 |
||
|
|
|
|
|
|
|
|||
lim e |
|
x 2 |
||
x 0 |
|
|
|
|
|
3 cos3x |
||
|
|
|
|
sin3x |
|||
|
|
||
|
|
|
1 |
|
|
|
|
|
|
|
x 2 |
|||
lim e |
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 2 |
|
|
3x 2 |
|
|
|
|
|
|
|
|
lim |
|
|||||
|
lim |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||||
|
x |
|
0 |
|
sin3x |
|
|
x 0 |
|
|
|
e |
|
|
|
|
e |
|
sin3x |
|
|||
|
|
|
|
|
|
|
|||||
|
|
6x |
|
|
|
lim |
|
|
e0 |
|
|
|
|
||||
e x 0 |
|
3 cos3x |
1 . |
||
|
|
|
1 |
|
1 |
|
|
Пример 3.25. Найти предел lim |
|
|
|
|
|
|
. |
|
2 |
|
|
||||
|
|
4 |
|
|
|
||
x 2 x |
|
|
ln x 1 |
||||
Решение:
|
|
|
1 |
|
1 |
|
lim |
ln x 1 x2 4 |
|
|
0 |
|
|||||
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
2 |
4 ln(x |
|
|
|
|
|||||||
|
|
4 |
|
|
|
|
1) |
|
|
|
|||||||
x 2 x |
|
|
ln x 1 |
x 2 |
|
|
|
0 |
|
||||||||
Производную можно применить к исследованию функций для построения ее графика.
Для определения интервалов возрастания и убывания функции применяют следующие теоремы.
Теорема (Необходимое условие возрастания (убывания)
функции). Если непрерывная и дифференцируемая |
на |
||
интервале |
a, b функция |
f x возрастает (убывает), то |
для |
любой точки этого интервала f x 0 f x 0 .
Теорема (Достаточное условие возрастания (убывания)
функции). Если функция f x непрерывна и дифференцируема
на интервале a, b и |
f x 0 |
( f x 0) для любого x a,b , |
то функция f x является |
возрастающей (убывающей) на |
|
интервале a, b . |
|
|
При исследовании функции необходимо определить наличие точек минимума и максимума.
46
Точка |
x0 называется |
точкой |
максимума |
(точкой |
||
минимума) |
функции |
y f x , |
если |
существует |
такая |
- |
окрестность точки x0 , |
что для всех остальных значений |
x из |
||||
этой окрестности будет выполняться неравенство
f x0 f x , ( f x0 f x ) .
Значение функции в точке максимума (минимума)
называется максимумом (минимумом) функции или экстре-
мумом функции.
Понятие экстремума функции является локальным для функции, поскольку всегда связано с определенной окрестностью точки из области определения функции.
Рассмотрим необходимое и достаточные условия существования экстремума функции.
Теорема (Необходимое условие экстремума). Если |
|
дифференцируемая функция y f x имеет в точке |
x x0 |
максимум или минимум, то ее производная обращается в нуль в этой точке, т. е.
f x0 0 (обратное не верно).
Геометрический |
смысл теоремы состоит в |
том, что |
в точке экстремума |
дифференцируемой функции |
y f x |
касательная к ее графику параллельна оси Ox .
Точки, в которых производная обращается в нуль,
называются стационарными.
Точки непрерывности, в которых производная функции равна нулю или не существует, называются критическими точками первого рода.
Теорема (Достаточное условие экстремума). Если |
||
функция |
y f x |
непрерывна в некоторой -окрестности |
точки x0 |
и при переходе через нее слева направо производная |
|
f x меняет знак с плюса на минус, то x0 есть точка макси-
47
мума; если же изменение знака происходит с минуса на плюс, то x0 является точкой минимума.
Еще одним из пунктов исследования функции является
определение интервалов выпуклости, вогнутости функции, точек перегиба.
График дифференцируемой функции y f x называется
выпуклым на интервале a,b , |
если любая касательная на этом |
интервале будет располагаться выше графика функции. График |
|
функции y f x называется |
вогнутым на интервале a,b , |
если любая касательная на этом интервале будет располагаться |
|
ниже графика функции. |
|
Точки графика непрерывной функции y f x ,
отделяющие участки вогнутости и выпуклости графика,
называются точками перегиба.
Интервалы выпуклости и вогнутости, точки перегиба
находят с помощью следующих теорем. |
|
|
||||||
Теорема. |
Если |
функция |
y f x |
в |
любой точке |
|||
интервала a,b имеет отрицательную вторую производную, |
||||||||
т. е. f x 0 , |
то график функции в этом интервале является |
|||||||
выпуклым. |
Если |
же |
вторая |
производная |
положительная |
|||
в любой точке интервала |
a,b , |
то график функции является |
||||||
вогнутым на этом интервале. |
|
f x непрерывной |
||||||
Если в точке |
x0 |
вторая производная |
||||||
функции |
y f x |
равна |
нулю |
или не существует, а при |
||||
переходе через точку |
x0 |
вторая производная меняет знак, то |
||||||
точка графика с абсциссой x0 является точкой перегиба.
Точки, где функция непрерывна, а вторая производная равна нулю или не существует, называются критическими точками второго рода.
Следующим пунктом в исследовании функции является
определение наличия асимптот. 48
Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки по кривой от начала координат.
Асимптоты могут быть вертикальными и наклонными.
Вертикальные асимптоты появляются на границах области определения функции и в точках разрыва второго рода.
Прямая |
x a |
является |
вертикальной асимптотой графика |
|||||
функции y f |
x , если |
lim |
f (x) или |
lim f (x) . |
||||
|
|
|
x a 0 |
x a 0 |
||||
|
|
|
|
|
||||
Наклонные асимптоты — это прямые с уравнением вида |
||||||||
y kx b |
при |
x , |
где параметры k и |
b находятся по |
||||
формулам: |
|
|
|
|
f x |
|
|
|
|
|
k lim |
|
; b lim f x kx . |
||||
|
|
|
|
|||||
|
|
|
x |
x |
x |
|
||
Если хотя бы один из пределов, связанных с вычислением |
||||||||
коэффициентов k и b , |
не |
существует или равен беско- |
||||||
нечности, то кривая |
y f x |
не имеет наклонной асимптоты. |
||||||
В частном случае, |
когда |
k 0 , получаем |
горизонтальную |
|||||
асимптоту. Существуют функции, графики которых имеют различные асимптоты при стремлении x к и , поэтому при определении параметров k и b необходимо вычислять соответствующие пределы при x и x .
Рассмотрим общий план исследования функции: 1) определяем область определения функции; 2) находим точки разрыва функции;
3) находим точки пересечения графика функции с осями координат, определяем четность (нечетность) функции, ее периодичность;
4) находим критические точки первого рода, в которых |
||
f (x) = 0 или |
f (x)` не существует, но функция |
y f x |
непрерывна, интервалы возрастания и убывания функции, точки экстремума функции;
49
