
Учебное пособие 1631
.pdf
Положим, x4 t . Тогда х2 = 2 – t, x3 = 8 – 3t, x1 = 11t – 27, x5 = 16t – 42.
20

2. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
Вектором называется направленный отрезок, обозначае-
мый или a , или AB с указанием начальной точки A (точки приложения) и конечной точки B (рис. 1) .
В
|
|
|
А |
AB |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 1 |
|
|
|
|
|
|
|
|
|
|
Длина (модуль) вектора AB обозначается | |
AB | . |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вектор 0 |
называется нулевым, |
если имеет длину, |
равную |
||||||||||
нулю. Нулевой вектор не имеет определенного направления. |
||||||||||||||
|
Векторы, лежащие на одной прямой или параллельных |
|||||||||||||
прямых, называются коллинеарными. |
|
|
|
|
|
|
|
|||||||
|
Векторы, лежащие на одной плоскости (или в парал- |
|||||||||||||
лельных плоскостях), называются компланарными. |
|
|||||||||||||
|
Пусть известны координаты точек начала и конца вектора |
|||||||||||||
A(x1, y1, z1 ) , B(x2 , y2 , z2 ) , |
тогда координаты вектора AB равны |
|||||||||||||
разностям координат конца и начала вектора, т. е. |
|
|
|
|||||||||||
|
|
AB {x2 x1, y2 y1, z2 z1} . |
|
|
|
|||||||||
|
Длина вектора AB равна |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
| AB | (x |
2 |
x ) |
2 ( y |
2 |
y )2 |
(z |
2 |
z )2 . |
|
||||
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сумма произведений n векторов a1 , a2 , |
…, |
an на |
|||||||||||
вещественные |
числа |
|
1, 2 , ...,n , |
|
а |
|
|
именно |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 a1 |
2 a2 ... n an |
|
называется |
линейной |
комбинацией |
|||||||||
векторов.
21
Если линейная комбинация векторов обращается в ноль
|
|
|
|
|
|
|
1 a1 2 a2 ... n an 0 |
при условии, |
что |
вещественные |
|||
числа 1, 2 , ..., n |
отличны от нуля, |
то вектора называются |
||||
|
|
|
|
|
|
|
линейно |
зависимыми. |
Векторы a1 , a2 ,…, an |
называются |
|||
линейно независимыми, если равенство нулю их линейной комбинации возможно лишь в случае, когда все числа1, 2 , ..., n равны нулю.
Теорема. Необходимым и достаточным условием линейной зависимости двух векторов является их коллинеарность.
Теорема. Необходимым и достаточным условием линейной зависимости трех векторов является их компланарность.
Базисом в пространстве называется максимально возможная по количеству линейно независимая система векторов. В трехмерном пространстве три некомпланарных
|
|
|
|
вектора a , |
b , |
c |
образуют базис. Тогда для любого вектора d |
всегда найдутся такие вещественные числа , , |
, что вектор |
|||||
|
|
|
|
|
|
|
d может |
быть |
представлен в |
виде линейной |
комбинации |
||
|
|
|
|
|
разложен по базису, где , |
|
векторов: |
d a |
b |
c , т. е. |
|||
, называются координатами вектора d в базисе векторов
a , b , c .
Разложение вектора d по базису данных векторов единственно.
Необходимость введения понятия базиса обусловлена тем, что линейные операции над векторами (сложения, вычитания, умножения на вещественное число) становятся операциями над числами (координатами этих векторов).
22
|
|
|
|
|
|
|
|
|
|
А |
именно: |
если |
d1 1 a |
1 b |
1 c 1 , 1 , 1 , |
||
|
|
{ 2 , 2 , 2 }, |
|
|
|
1 2 , 1 2 , 1 2 , |
||
а |
d2 |
то |
d 1 + d 2 |
|||||
|
|
1 , 1 , 1 |
. |
|
|
|
|
|
а d 1 |
|
|
|
|
|
|||
|
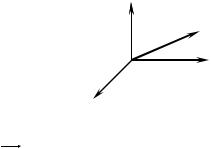
Декартовая прямоугольная система координат (рис. 2) |
|||||||
представляет собой |
три |
взаимно |
перпендикулярные оси |
|||||
в пространстве с общим началом О и одинаковой масштабной единицей: ось Оx — ось абсцисс; ось Оy — ось ординат; ось
Оz — ось аппликат.
z
A
О
y
x
Рис. 2
Вектор OA , выходящий из начала координат, называется
радиус-вектором.
Декартовой прямоугольной системе координат отвечает тройка взаимно ортогональных единичных базисных векторов
|
|
|
|
(ортов) i , |
j , |
k . Для произвольного вектора |
d найдется |
единственная тройка чисел x, y, z , такая, что будет справедливо
|
|
|
|
|
|
|
|
|
|
|
равенство |
d xi y j z k , где |
i |
{1,0,0} , |
|
j |
{0,1,0} , |
||||
|
{0,0,1} , |
|
|
|
|
|
|
|
|
|
k |
x, y, z — декартовые прямоугольные координаты d , |
|||||||||
|
{x, y, z}. |
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
||
|
Скалярным |
произведением двух |
векторов |
|
называется |
|||||
|
|
|
|
|
|
|
|
|
|
|
число, обозначаемое как |
( a, b ) и равное ( a, b ) | a | |
| b | cos , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
где — угол между a |
и |
b . |
|
|
|
|
|
|||
|
|
|
|
|
23 |
|
|
|
|
|
|
Скалярное |
|
произведение |
обладает |
следующими |
|||||||
свойствами: |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
|
1. |
( a, b ) |
( b, a ) . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
2. |
( a, b ) |
( a, b ) . |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
3. |
( a |
b , c) ( a, c ) |
|
( b, c ) . |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
( a, a ) |
0 , если a |
— ненулевой вектор, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Если |
заданы координаты |
векторов |
a ax , ay , az , |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b bx , by ,bz , |
|
то их скалярное произведение равно сумме |
||||||||||
произведений |
|
их |
соответствующих |
координат, т. е. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(a,b) axbx ay by az bz . |
|
|
|
|
|
|
||||||
|
Пример |
2.1. |
Фермер |
производит 5 |
видов |
продукции |
||||||
П1, |
П2, |
П3, |
П4, |
П5 |
в количествах 40, 60, |
10, |
80, |
20 единиц. |
||||
При этом нормы расхода сырья составляют соответственно 10; 2; 5, 8, 6 единиц. Определить расход сырья на всю продукцию и его изменение при изменениях выпуска
продукции П1, П2, П3, П4, П5 |
соответственно +10, -15, +10, -10, |
|||
+5 единиц. |
|
|
|
|
Решение. Обозначим |
вектор |
выпуска |
продукции |
|
|
, а вектор расхода сырья |
|
|
|
b bx ,by ,bz |
y 10,2,5,8,6 . Тогда |
|||
суммарный |
расход сырья |
S есть скалярное |
произведение |
|
|
|
|
|
|
векторов x и y , т. е.
|
10 |
60 2 10 5 80 8 20 6 |
850 |
(ед.). |
S x, y 40 |
Применяя свойство скалярного произведения, изменение суммарного расхода сырья можем записать:
S = ( x + x , y ) – ( x , y ) = ( x , y ) = 10 · 10 –
– 15 · 2 + 10 · 5 – 10 · 8 + 5 · 6 = 70. 24
Рассмотрим метод решения систем линейных неравенств.
Поскольку система состоит из отдельных неравенств, рассмотрим, что собой представляет решение линейного неравенства.
Решим линейное неравенство с двумя переменными x1 и x2: a1x1 a2 x2 b 0 . Здесь переменные x1 и x2 можно представить как координаты точки на плоскости. Тогда совокупность точек, удовлетворяющих данному неравенству, представляет собой область решений данного неравенства (полуплоскость).
Приведя неравенство к виду x2 kx1 l или x2 kx1 l ,
можно определить, какая именно полуплоскость является областью решений неравенства.
Если x2 kx1 l , то искомая полуплоскость лежит выше прямой x2 kx1 l , а если x2 kx1 l , то ниже ее.
Система неравенств дает пересечение конечного числа полуплоскостей, которое образует многоугольную область,
называемую областью решений системы неравенств. Эта область может быть как ограниченной, так и неограниченной, и даже пустой.
Пример 2.2. Найти область решений системы неравенств
x1 2 0,
x2 2x1 0,
x1 x2 2 0,
6x1 12x2 36 0.
Решение. Преобразуем неравенства в уравнения: x1 – 2 = 0, x2 – 2x1 = 0, x1 + x2 – 2 = 0, -6x1 – 12x2 + 36 = 0,
получив |
уравнения прямых, |
которые построим на |
графике |
|
(рис. 3). |
|
|
|
|
Приведем данные неравенства к виду x1 2 , |
x2 2x1 , |
|||
x2 x1 |
2 , |
x2 ( 1/ 2)x1 |
3 . Полуплоскости, |
которые |
|
|
|
25 |
|
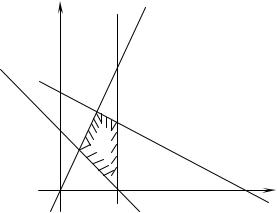
являются решением неравенств, отметим штриховкой. Тогда из графика видно, что областью решений системы неравенств является выпуклый четырехугольник ABCD.
x2
В
С
А
 D
D
0 |
x1 |
Рис. 3
26
3. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
Пусть X |
и Y — некоторые числовые множества. Если |
|
каждому значению |
x из множества X ( x X ) ставится |
|
в соответствие |
по |
определенному правилу f значение y |
из множества Y ( y Y ), то говорят, что задана функциональная
зависимость или однозначная функция y от |
x , а именно |
y f x . Значение x называется независимой |
переменной |
(аргументом), y — зависимой переменной, множество X — областью определения функции, множество Y — областью значения функции.
Функцию можно задать тремя способами: табличным,
аналитическим и графическим.
Табличный способ. Этот способ широко используется при экспериментальных измерениях различных величин в науке и технике. В таблицах одну из переменных принимают за независимую переменную или аргумент, тогда другие величины будут функциями от этого аргумента. Табличный способ задания функциональной зависимости широко используется в различных базах данных.
С помощью методов аппроксимации по данным таблицы можно приближенно установить аналитический способ задания функции.
Аналитический способ. Этот способ состоит в формульном задании связи между аргументом и функцией y f x .
Графический способ. При графическом способе задания функции связь между аргументом и функцией задается посредством графика. Графиком называется множество точек координатной плоскости, абсциссами которых являются значения аргумента, а ординатами — соответствующие значения функции.
27

Основные элементарные функции: степенная функция x ( – любое действительное число), показательная функция
y a x (a 0, a 1) , |
|
логарифмическая |
функция |
|
y loga x 0 a 1 , |
|
тригонометрические |
функции |
|
y sin x, y cosx, |
y tgx, y ctgx |
и обратные |
тригоно- |
|
метрические функции |
y arcsin x, |
y arccosx, |
y arctgx, |
|
y arcctgx. |
|
|
|
|
Функции, полученные с помощью конечного числа алгебраических (сложение, вычитание, умножение, деление, возведение в степень с целым показателем, извлечение корня) и трансцендентных (возведение в степень с иррациональным показателем, логарифмирование, вычисление значений тригонометрических и обратных тригонометрических функций) операций, также являются элементарными.
Алгебраическими называются элементарные функции, полученные с помощью конечного числа алгебраических операций. Алгебраические функции подразделяются на рациональные и иррациональные функции. К рациональным функциям относятся целая и дробная рациональные функции. Функция вида
P x a0 xn a1xn 1 a2 xn 2 an 1x an ,
где n — натуральное число или ноль, a0 , a1 , a2 , , an — любые
действительные числа (коэффициенты), называется целой рациональной функцией, или алгебраическим многочленом степени n.
Многочлен первой степени называется линейной функцией.
Отношение двух целых рациональных функций
R x a0 xn a1xn 1 an 1x an b0 xm b1xm 1 bm 1x bm
называется дробно-рациональной функцией. 28
Алгебраическая функция, содержащая аргумент под знаком радикала, называется иррациональной функцией,
например, функция f x 
 6x 1 x7 / 9 является иррацио-
6x 1 x7 / 9 является иррацио-
нальной.
Алгебраические функции, не являющиеся рациональными
или иррациональными, называются трансцендентными |
||
функциями, например, |
функции |
f x sin 8x ln 2x и |
x 45x arctgx являются трансцендентными. |
||
Сложной функцией |
(функция от |
функции) называется |
такая зависимость у от х, что у является функцией от переменной u (промежуточный аргумент), а u , в свою очередь, зависит от переменной x . Функция вида y 
 ln x представляет собой пример сложной функции, где в качестве промежуточного аргумента выступает u ln x . Существуют сложные функции, содержащие несколько промежуточных
ln x представляет собой пример сложной функции, где в качестве промежуточного аргумента выступает u ln x . Существуют сложные функции, содержащие несколько промежуточных
|
|
|
|
аргументов. Например, |
в функции y sin log4 x |
функция |
|
y sin u зависит от |
первого промежуточного |
аргумента |
|
u 
 v , а v является вторым промежуточным аргументом, т. е.
v , а v является вторым промежуточным аргументом, т. е.
v log4 x . |
y f x |
|
|
Функция |
называется |
возрастающей |
(убывающей) в некоторой области, если для любых значений
аргумента функции x1 |
и |
x2 , удовлетворяющих условию |
|||
x2 |
x1 |
( x2 < x1 ) будет |
выполняться условие |
f x2 f x1 |
|
( f |
x2 f x1 ). |
|
|
|
|
|
Если же неравенству |
x2 x1 соответствует |
f x2 f x1 |
||
( f x2 f x1 ), то функция |
y f x называется неубывающей |
||||
(невозрастающей).
Функция, удовлетворяющая одному из вышеназванных определений, называется монотонной.
29
