
Методы оптимизации технологических процессов. Кузовкин А.В., Кузовкин В.П
.pdf
если f``(xk) > 0, то в точке xk достигается минимум функции f(x); если f``(xk) < 0, то в точке xk достигается максимум функции f(x).
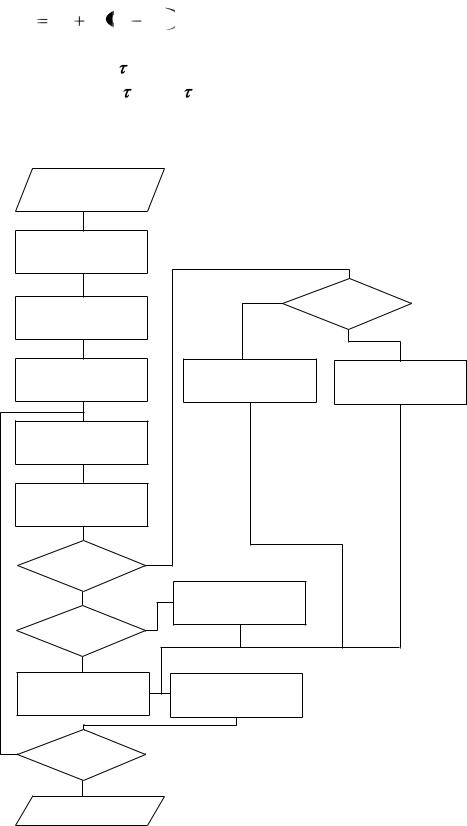
Алгоритм нахождения экстремума функции по методу Ньютона представлен на рис.6.6.
Ввод |
|
|
Требуемая точность Е |
|
|
исходных |
|
|
|
|
|
|
|
Начальное значение Х |
|
||
данных |
|
|
0 |
||
|
|
|
|
Вид функции f(x) |
|
|
|
|
|
|
|
Xi = Xo |
Да |
|
|
|
|
Xi=X i+1
F'(Xi)
Если |
Нет |
|
|
|X i+1-Xi| |
> E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F"(Xi+1) |
|
|
|
|
|
|
F''(Xi) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Да |
|
|
||
|
|
|
|
|
Если |
X i+1 - min |
|||||
|
|
|
|
|
F"(X i+1)>0 |
|
|
|
|||
X i+1 =Xi-(F'(Xi)/F"(Xi) |
|
|
|
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi+1 - max |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод |
|
|
|
|
|
|
|
|
|
|
результатов |
|
|
|
|
|
||
Рис. 6.6. Алгоритм определения экстремума методом Ньютона ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Задание на лабораторную работу студент выбирает из табл. 6.3 в соответствии со своим порядковым номером в списке группы.
2.Опираясь на теоретические сведения студент составляет программу на языке программирования Paskall (или любом другом) для решения задачи поиска экстремума функции методом Ньютона. Программа и ее результаты после отладки и проверки должны быть приложены к отчету.
3.Составляется программа построения кривой функции f(x) с масштабом, достаточным для проверки результатов расчетов по п.2 (можно использовать средства построения графиков функций других приложений - Excel-97 или
MathcadPLUS-6.0).
СОДЕРЖАНИЕ ОТЧЕТА 1. Название и цель работы, краткие теоретические сведения о методе
Ньютона.

2.Заданная функция, ее первая и вторая производные.
3.Блок-система алгоритма.
4."Листинг" программы и результаты ее выполнения.
5.Результат выполнения программы построения кривой заданной функции и сравнение полученных данных со значениями, полученными с помощью любого стандартного программного обеспечения.
6.Выводы по работе.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 6.3 |
||
|
Варианты задания для лабораторной работы № 2 |
|
|
|
|
|
|
|
||||||||||||||||||||
№ |
Функция |
№ |
|
Функция |
||||||||||||||||||||||||
варианта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
варианта |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x2 |
|
|
|
Sinx |
15 |
|
e x |
|
Cosx |
||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
x 2 |
|
|
|
Cosx |
16 |
|
ex |
Cosx |
||||||||||||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
x 2 |
|
4Sinx |
17 |
|
e x |
Sin2x |
|||||||||||||||||||||
4 |
3x |
|
|
4tgx |
18 |
|
e x |
|
|
Sinx |
||||||||||||||||||
5 |
|
|
x |
Cosx |
19 |
|
ex |
Sinx |
||||||||||||||||||||
6 |
4x2 |
|
|
Cosx |
20 |
|
ex |
4Cos2x |
||||||||||||||||||||
7 |
|
|
x 2 |
|
|
Sinx |
21 |
|
e x |
Sinx |
||||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
0,85x0,5 |
|
|
0,3tgx |
22 |
|
|
|
|
x |
ex |
|||||||||||||||||
9 |
|
|
x(x |
|
|
1)2 |
|
23 |
|
x2 |
ex |
|
|
Sinx |
||||||||||||||
10 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
24 |
|
|
tgx |
|
ex |
||||||||
|
|
|
|
|
x 2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
11 |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
25 |
|
tg( |
x) |
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
||||||||
|
|
|
|
(x |
|
1)2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
12 |
|
|
x 2 (x |
1) |
26 |
|
|
|
|
|
tgx |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2x 2 |
|
|
|
|
||
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27 |
|
|
|
Sin2 x |
||||||||
|
|
|
|
|
|
x |
1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x 2 |
1 |
|
|
x |
|
|
Cosx |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ |
|
|
|
|
|
|
|
|
|
|
|
||||
1. Поясните порядок поиска точки экстремума функции методом Ньюто-
на.
2.Ни каких соображений выбирается значение начальной точки для аппроксимации корня?
3.По какому выражению ищется каждое последующее значение аппроксимируемого корня?
6.3. Лабораторные работы № 3 и 4. Поиск оптимума методом Фибоначчи и "золотого сечения"
Цель работы: Теоретическое изучение и получение практических навыков отыскания оптимума функции методом Фибоначчи.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Часто существуют задачи, которые не дают возможности определить экс-
тремум функции классическими методами. Это может быть пример, когда решить уравнение и найти его корни традиционным способом не удается. В этом случае с помощью численных методов экстремум функции f(x) ищется непосредственно в некотором интервале a < x0 < b, в котором как предполагается лежит экстремум.
Пусть точки а и в определяют интервал, в котором лежит истинная точка минимума и внутри этого интервала функция унимодальная, т.е. имеет только один экстремум (рис. 6.7). В интервале [а, b] известны значения функции в трех точках x1, x2, x3, таких что a < x1 < x2 < x3 < b, f(x2) < f(x1), f(x2) < f(x3).
|
|
|
Y |
|
|
|
a |
X1 |
X 4 |
X m |
X 2 |
X 3 |
b X |
|
Рис. 6.7. Поиск экстремума функции методом Фибоначчи
Тогда точка xm лежит внутри интервала (x1, x3), меньшем чем (а, b). Внутри отрезка (x1, x3) мы можем вычислить функцию в точке x4, но сде-
лать это только один раз. При этом точка x4 помещается внутри отрезка (x1, x3) симметрично точке x2, т.е. длины (x1, x2) и (x4, x3) должны быть одинаковы. После этого следует переходить к рассмотрению отрезка (x1, x2) или (x4, х3), которые меньше начального интервала (x1, x3) а точка экстремума лежит заведомо внутри этих интервалов.
Координата точки x2 при известном начальном интервале (x1; x3) определяется по выражению:
|
|
F |
|
|
|
|
1 n |
|
|
x |
|
n 1 |
x |
|
x |
|
|
; |
(6.12) |
2 |
|
3 |
1 |
|
|||||
|
Fn |
|
|
Fn |
|
||||
|
|
|
|
|
|
|
|||
где n - количество вычислений, которые необходимо выполнить;
 - минимально возможное расстояние между двумя точками, возможно
- минимально возможное расстояние между двумя точками, возможно
=0;
Fn, Fn-1 - числа Фибоначчи, которые определяются как: F0 = 1, F1 = 1, Fn = Fn-1
+ Fn-2.

Последующее определение координаты точки x4 в числах Фибоначчи не нуждается и осуществляется по выражению:
x4 x1 x2 x3 |
(6.13) |
Обозначим f(x2) = Y2 и f(x4) = Y4 и рассмотрим 4 возможных варианта взаимного расположения точек x2, x4 и значений функций Y2, Y4 (рис.6.8).
|
|
|
|
Y4 |
2 |
|
|
|
|
|
|
|
|
Y |
Y |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
а) |
|
|
|
|
|
|
|
|
б) |
|
2 |
4 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
X1 X4 X 2 X 3 |
|
X1 X 2 X 4 X 3 |
|||||||||||||||||||||
|
|
|
|
X4 |
< |
X 2 |
|
|
|
|
X 2 |
< |
|
X4 |
||||||||||
|
|
|
|
Y4 |
< |
Y2 |
|
|
|
|
Y4 |
< |
|
Y2 |
|
|
|
|||||||
в) |
|
Y4 |
Y2 |
|
г) |
|
|
Y2 Y4 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
X1 X4 X 2 X 3 |
|
|
|
|
X1 X 2 X 4 X 3 |
||||||||||||||||||
|
|
|
|
X4 |
< |
X 2 |
|
|
|
|
|
|
X2 |
< |
X4 |
|||||||||
|
|
|
|
Y |
< |
Y4 |
|
|
|
|
|
|
Y |
< |
Y |
4 |
|
|||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||
Рис. 6.8. Возможные варианты выбора значения координат точек и значений функций
Проанализировав рис. 6.8 можно сделать вывод о том как происходит выбор интервалов для последующих итераций. Для ситуации (рис. 6.8 а) выбираем новый интервал (x1, x2), содержащий точку x4. Для (рис. 6.8 б) выбираем интервал (x2, x3), содержащий точку x4. Для рис. 6.8 в выбираем новый интервал (x4,x3), содержащий точку x2, а для рис. 6.8 г выбираем интервал (x1, x4) содержащий точку x2.
Процесс выбора оптимального, в случае поиска минимума, значения функции методом Фибоначчи может быть реализован в соответствии с алгоритмом, изображенном на рис. 6.9.
Частным случаем метода Фибоначчи является метод “золотого сечения”, особенностью которого является то, что не нужно знать количество вычислений функции “n”. При этом принимают отношения интервалов постоянным:
|
L j 1 |
|
L j |
|
L j 1 |
... |
, |
(6.14) |
|
L j |
|
L j 1 |
|
L j 2 |
|||
|
|
|
|
|
|
|||
где Lj - длина отрезка, полученного при j-ом делении; |
|
|||||||
- постоянная, характеризующая “золотое сечение”, |
= 1,618033989. |
|||||||
При таком делении исходного отрезка (x0, x3) (рис. 6.10) на три участка
две последующие точки x1 и x2 |
вычисляются по выражению: |
|
x1 |
x0 t1 x3 x0 , |
(6.15) |
x2 x0 t 2 x3 |
x0 , |
(6.16) |
где t1, t2 - коэффициенты “золотого сечения”, соответственно равные: |
|
|
t1 = 2 - |
|
(6.17) |
t2 = 1 - t1 = 1 - 2 + |
= -1 + |
(6.18) |
Алгоритм поиска минимума функции методом "золотого сечения" представлен на рис. 6.11.
Ввод |
|
|
|
исходных |
|
|
|
данных |
|
|
|
Определение |
|
|
|
чисел |
|
|
|
Фибоначчи |
|
|
|
|
|
Нет |
|
Определение |
|
X2 < X4 |
|
|
|
||
Х2 по выраж. (3.1) |
|
Да |
|
|
|
|
|
Вычисление |
|
X3 = X4 |
|
F(X2) |
X1 = X4 |
||
Вычисление |
|
|
|
Х4 по выраж. (3.2) |
|
|
|
Вычисление F(X4) |
|
|
|
|
Да |
|
|
F(X4) > F(X2) |
|
|
|
|
Нет |
X1 = X2 |
|
|
X2 = X4 |
|
|
|
|
|
|
|
Да |
F(X2) = F(X4) |
|
X2 < X4 |
|
|
|
|
Нет |
|
|
X3 = X2 |
X2 = X4 |
K = K + 1 |
|
F(X2) = F(X4) |
|
||
|
|
||
Да |
|
|
|
K < N |
|
|
|
|
Нет |
|
|
Конечное |
|
|
|
значение F(X2) |
|
|
|
Рис. 6.9. Алгоритм поиска оптимума методом Фибоначчи

F(X0) |
|
F(X2) F(X3) |
F(X0) |
|
|
|
F(X3) |
|||||||||||||||
|
|
F(X1) |
|
|
|
|
|
|
|
|
F(X1) |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(X2) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X0 |
X |
X |
2 |
X |
3 |
|
|
X 0 |
X1 |
X |
2 |
X |
|||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
Рис. 6.10. Варианты деления начального отрезка (x0, x на три части: а) при следующих вычислениях переходим к отрезку (x1; x3); б) при последующих вычислениях к отрезку (x0; x2).
на три части: а) при следующих вычислениях переходим к отрезку (x1; x3); б) при последующих вычислениях к отрезку (x0; x2).
|
Ввод |
|
|
|
исходных |
|
|
||
данных |
|
|
||
Вычисление |
|
|
||
t1 |
и |
t2 |
|
|
Определение |
|
|
||
X1 |
X2 |
|
|
|
Вычисление |
|
|
||
F(X1) |
и |
F(X2) |
|
|
|
|
|
Да |
|
F(X1) < F(X2) |
|
|
||
|
Нет |
|
|
|
I=X2-X0 |
X3=X2 |
I=X3-X1 |
X0=X1 |
|
X2=X1 |
X1=X0+t1*I |
X1=X2 |
X2=X0+t2*I |
|
F(X2)=F(X1) |
F(X1)=F(X2) |
|||
Да |
|
|
|
|
I > E |
|
|
|
|
|
Нет |
|
|
|
Xm=X1 или Xm=X2 |
|
|
||
F(X1) |
или |
F(Xm) |
|
|
Вывод |
|
|
|
|
Xm |
и |
F(Xm) |
|
|
Рис. 6.11. Алгоритм решения задачи по методу “золотого сечения”

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Заданием на лабораторную работу является выражение, исследование которого студент проводил при выполнении лабораторной работы № 2. Используя точки экстремума, определенные ранее, необходимо выбрать интервал, на котором будет осуществляться поиск точки минимума функции.
2.Опираясь на теоретические сведения и алгоритм, приведенный на рис.
6.9.разрабатывается программа вычисления точки экстремума функции методом Фибоначчи. Программа после проверки ее работы прикладывается к отчету. По результатам вычислений точек минимума заполняется табл. 6.4.
3.Аналогичная работа проделывается для метода “золотого сечения”, при чем вычисления по этому методу производятся с различной точностью, а результаты расчета распечатываются и сводятся в табл. 6.4.
|
|
|
|
|
|
Таблица 6.4 |
||
|
|
Результаты определения экстремума функции |
|
|
|
|||
Точка |
№ вы- |
Количество |
Минимально воз- |
метод |
метод “зо- |
|
метод |
|
мини- |
числе- |
приближе- |
можное расстояние |
Фибонач- |
лотого се- |
|
Ньюто- |
|
мума |
ния |
ний N |
между точками |
чи |
чения” |
|
на |
|
|
1 |
30 |
0 |
|
|
|
|
|
1 |
2 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
30 |
0,005 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
5 |
30 |
0 |
|
|
|
|
|
2 |
6 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
7 |
30 |
0,005 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
8 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
. . . . |
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
СОДЕРЖАНИЕ ОТЧЕТА
1.Название и цель работы, краткие теоретические сведения по методу "Фибоначчи" и "золотого сечения".
2.Заданная функция и алгоритм. Определение точки минимума методом Фибоначчи и методом “золотого сечения”.
3.Распечатку программ и результатов выполнения, а также заполненную таблицу 6.4.
4.Алгоритм поиска точки максимума функции, распечатку программы реализующую процедуру поиска, результаты и заполненную табл. 6.4.
5.Выводы по работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Для каких случаев целесообразно применение метода Фибоначчи?
2.Поясните порядок деления отрезка с использованием числа Фибонач-
чи.

3.Какие варианты могут возникнуть при выборе четвертой точки в от-
резке?
4.Запишите выражения для определения чисел Фибоначчи и точки при поиске точки максимума функции методом Фибоначчи.
5.В чем сходство и в чем отличие поиска оптимума функции методами Фибоначчи и “золотого сечения”?
6.4. Лабораторная работа № 5. Определение экстремума функции с помощью аппроксимации кривыми
Цель работы: Теоретическое изучение и получение практических навыков применения квадратичной интерполяции при поиске экстремума функции.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ Решение задачи поиска экстремума функции методом квадратичной ин-
терполяции выполняется следующим образом. В качестве начальных условий используется начальное значение X1, шаг аппроксимации h и требуемая точность вычисления E.
Если известны значения функции в трех различных точках X1, Х2, Х3 которые соответственно равны F1, F2, F3, то такую функцию можно аппроксимировать квадратичной функцией Y(X) вида:
Y ( X ) AX BX C , |
(6.19) |
где A, B, C - коэффициенты, которые определяются из выражений:
|
|
A |
( X 3 |
X1 )F1 ( X1 |
X 3 )F2 |
( X |
2 |
X1 )F3 |
(6.20) |
|||||||
|
|
|
|
( X1 |
|
X 2 )( X 2 |
X 3 )( X 3 |
X1 ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
( X 2 |
X 2 )F ( X 2 |
X 2 )F ( X |
2 |
X 2 )F |
|
||||||||
|
B |
|
2 |
3 |
1 |
3 |
1 |
2 |
1 |
2 |
3 |
|
(6.21) |
|||
|
|
|
|
( X1 |
X 2 )( X 2 |
X 3 )( X 3 |
X1 ) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||
C |
X 2 X 3( X 3 |
X 2 )F1 |
X1 X 3( X1 |
X 3 )F2 |
|
X1 X 2 ( X 2 X1 )F3 |
(6.22) |
|||||||||
|
|
|
|
( X1 |
X 2 )( X 2 |
X 3 )( X 3 |
|
X1 ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
Вычислив первую производную функции Y(X) и решив уравнение Y'(X) = 0, мы получим корень Xi, являющийся точкой экстремума как функции Y(X), так и функции F(X). Решением такого уравнения является точка X4.
|
1 |
|
( X 2 |
X 2 )F ( X 2 |
X 2 )F ( X 2 |
X 2 )F |
|
||||
X 4 |
|
[ |
|
2 |
3 1 |
3 |
1 2 |
1 |
2 3 |
] |
(6.23) |
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
( X1 |
X 2 )F3 |
( X 2 |
X 3 )F1 |
( X 3 |
X1 )F2 |
|
|
Выражение (6.23) дает хорошие результаты при первой аппроксимации корня. Однако если точность вычисления задана высокой, а X1, X2, X3 и F1, F2, F3 близко расположены друг к другу, для вычисления координат X4 предлагается использовать следующее выражение:
X 4 |
( X 1 X 2 ) |
( F1 |
F2 )( F2 |
F3 )( F3 |
F1 ) |
. |
(6.24) |
||
2 |
|
2[( X 2 X 3 )F1 |
( X 3 |
X 1 )F2 |
( X 1 |
X 2 )F3 ] |
|
|
|
|
|
|
|||||||
После того как аппроксимация проведена один раз необходимо из существующих четырех точек X1...X4 отбросить одну и повторить вычисление новой

точки X4 еще раз. Эта процедура выполняется до тех пор, пока не будет достигнута точность вычислений.
На рис. 6.12 представлен алгоритм, реализующий поиск минимума функции методом квадратичной интерполяции.
Ввод на- |
Начальное значение Х1 |
|
Шаг h |
||
чальных |
||
Точность Е |
||
данных |
||
|
||
|
|
Вычисление f(x1); x2=x1+h; f(x2)
Если f(x1) f(x2)
Вычисление х3=х1+2h; f(x3)
Вычисление х4; f(x4)
Выбор двух наименьших значе-
ний f(xi) и f(xk)
Вычисление х3=х1-h; f(x3)
Выбор новых точек
Если |
Вычисление |
||
х4 |
и f(x4) |
||
f(x1) f(x2) |
|||
|
|
||
|
|
|
|
Вывод результата
Рис. 6.12. Алгоритм поиска минимума функции методом квадратичной интерполяции

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1.Заданием на лабораторную работу является функция, полученная студентом на второй лабораторной работе.
2.Опираясь на теоретические сведения и алгоритм, представленный на рис. 4.1 необходимо разработать алгоритм поиска максимума функции и программы вычисления точек экстремума функции методом квадратичной интерполяции. Так же необходимо определить коэффициенты аппроксимирующего уравнения А, В и С и записать аппроксимирующую функцию.
3.По результатам вычисления заполняется табл.6.5.
Таблица 6.5 Результаты поиска экстремума функции методом квадратичной интерполяции
Точка |
|
Метод Фибоначчи |
|
Метод квадратичной интерполяции |
||||
экстре- |
Количе- |
Расхожде- |
Хэкст |
F(Хэкст) |
Шаг h |
Точность Е |
Хэкст |
F(Хэкст) |
мума |
ство |
ние между |
|
|
|
|
|
|
|
прибли- |
точками |
|
|
|
|
|
|
|
жений N |
|
|
|
|
|
|
|
1 |
30 |
0 |
|
|
0,5 |
0,001 |
|
|
|
100 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
30 |
0,005 |
|
|
0,05 |
0,0001 |
|
|
|
100 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
…… |
|
|
|
|
|
|
|
|
n |
30 |
0 |
|
|
0,5 |
0,001 |
|
|
|
100 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
30 |
0,005 |
|
|
0,05 |
0,0001 |
|
|
|
100 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
СОДЕРЖАНИЕ ОТЧЕТА
1.Название и цель работы. Краткие теоретические сведения о методе поиска оптимума функции.
2.Функция и алгоритмы поиска точек экстремума. Таблица и аппроксимирующая функция.
3.Распечатка программ и результатов их выполнения, табл.6.5.
4.Выводы по работе.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.В каких случаях используется метод квадратичной интерполяции для поиска максимума или минимума функции.
2.Запишите уравнения для определения коэффициентов аппроксимирующего уравнения.
3.Покажите на примере стандартного программного обеспечения возможности получения аппроксимирующих уравнений.
4.Приведите алгоритм для поиска максимума (минимума) функции с использованием квадратичной интерполяции.
