
Учебное пособие 1499
.pdf
|
a1 |
|
a 0 |
|
|
1 |
|
a1 b2 |
|
a0 b2 |
|
b2 |
|
|
|
|
a 2 ; c b1 |
b0 |
; d |
. |
|||||||
A |
a 2 |
|
a 2 ; b |
|
|||||||||
|
|
|
|||||||||||
|
|
|
|
|
|||||||||
|
1 |
0 |
|
0 |
|
a 2 |
a 2 |
a 2 |
|||||
|
|
|
|
|
|
|
|
|
|||||
Аналогичные процедуры можно выполнить и для передаточных функций любого порядка. В общем случае для передаточной функции n-го порядка можно записать
|
|
|
|
|
b |
n |
|
pn |
b |
n 1 |
pn 1 |
... |
b |
p |
b |
0 |
|
|
|
|
||||||
|
|
|
W(p) |
|
|
|
|
|
|
|
|
|
1 |
|
|
. |
|
(1.18) |
||||||||
|
|
|
|
|
|
pn |
|
|
|
|
pn 1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
a n |
|
a n 1 |
... |
a1 |
p |
a 0 |
|
|
|||||||||||||
Системная матрица A для (1.18) будет представлять собой |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
a n 1 |
|
|
|
a n 2 |
|
... |
|
a1 |
|
a 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a n |
|
|
|
a n |
|
a n |
a n |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
... |
|
0 |
|
0 |
|
|
|
|
|
|
||
|
|
|
|
A |
|
0 |
|
|
|
1 |
|
... |
|
0 |
|
0 |
. |
|
|
|
|
(1.19) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
: |
|
|
|
|
: |
|
... |
|
: |
|
: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
... |
|
1 |
|
0 |
|
|
|
|
|
|
|||
Входной вектор |
Выходной вектор |
|
|
|
|
|
|
Коэффициент сквозной |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
передачи управления |
||||||||
|
|
|
|
bn 1 |
|
|
|
a n 1 |
bn |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
a n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a n |
|
|
bn |
|
|
|
|
a n |
2 |
bn |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
a n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0 |
; |
c |
т |
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
d |
|
|
bn |
. |
(1.20) |
||
b |
|
|
|
|
|
a n |
|
bn |
|
|
|
|
|
|
|
|
||||||||||
0 |
bn |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
a n |
|||||||||||
|
|
|
3 |
|
|
|
a n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
: |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
b0 |
|
|
|
a 0 |
bn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
a n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Следует заметить, что порядок системы определяется по степени полинома знаменателя и степень полинома числителя не должна превышать степень полинома знаменателя. Выражения (1.19, 1.20) позволяют представить любую передаточную функцию в векторно-матричной форме.
При составлении выражений (1.19, 1.20) по передаточным функциям и структурным схемам следует пользоваться следующими правилами /4/:
1)наддиагональные элементы системной матрицы А характеризуют передачу сигналов по прямой цепи связи;
2)диагональные – по цепи основных обратных связей;
3)поддиагональные элементы матрицы – по всем остальным цепям обратных связей;
21

4) элементы векторов b определяют воздействия на переменные состоя-
ния;
5) элементы строки cт указывают долю вклада сигналов состояния в сигнал выхода системы.
1.4.2.Взаимосвязь векторно-матричной формы описания объекта с его передаточной функцией
При исследовании динамических свойств систем автоматизированного электропривода (САЭП), как уже отмечалось, достаточно широко используются передаточные функции объектов, поэтому порой возникает необходимость перехода от векторно-матричной формы к описанию объекта в виде передаточной функции. Прежде всего, любую систему, описанную уравнениями состояния в обычной векторно-матричной форме (1.9), приводят к нормальной форме, в которой нормальные уравнения состояния записываются в виде
|
|
|
YH |
AH |
YH |
bH |
|
U , |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
H |
cT |
Y . |
|
|
|
|
(1.21) |
||
|
|
|
|
|
|
H |
H |
|
|
|
|
|
|
|
В качестве примера рассмотрим систему уравнений состояния |
||||||||||||||
|
|
Y1 |
a11 |
Y1 |
|
b1 U, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y2 |
Y1 |
a 22 Y2 |
a 23 Y3 |
|
a 24 Y4 , |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y3 |
a 21Y1 |
Y2 |
a33 Y3 |
|
a34 Y4 , |
|
(1.22) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y4 |
Y3 |
a 44 Y4 , |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
c1 Y1 c4 |
Y4 , |
|
|
|
|
|
|
|
|||
которая в обычной векторно-матричной форме записывается |
|
|
||||||||||||
|
|
|
|
Y |
A Y |
b U , |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
cT |
Y, |
|
|
|
|
|
(1.23) |
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a11 |
0 |
0 |
0 |
|
|
|
b1 |
|
|
|
|
|
|
A |
1 |
a 22 |
a 22 |
a 24 |
|
; |
b |
0 |
; |
c |
T |
c 0 0 c |
|
, |
|
|
|
|
|
|
|
4 |
|||||||
|
a 21 |
1 |
a33 |
a34 |
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
0 |
1 |
a 44 |
|
|
|
0 |
|
|
|
|
|
|
Y1 Y4 переменные состояния.
Системе уравнений (1.22) соответствует структурная схема, представленная на рис.1.11.
Используя матрицу преобразования в виде матрицы управляемости G b A  b A2
b A2 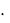 b An 1
b An 1 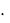 b , можно определить в нормальной форме матрицу AH и векторы bH и cH путем линейных преобразований /4/:
b , можно определить в нормальной форме матрицу AH и векторы bH и cH путем линейных преобразований /4/:
AH GT 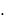 A
A 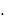 G ; bH GT
G ; bH GT 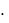 b ; cH G
b ; cH G 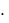 c .
c .
22

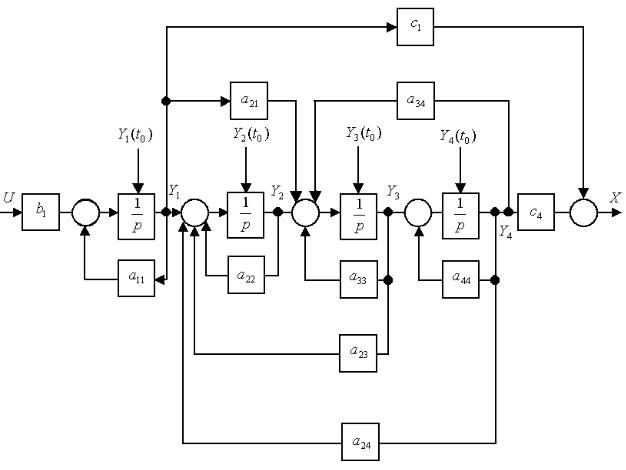 Р ис.1.11. Структурная схема САР, описанной уравнениями (1.22)
Р ис.1.11. Структурная схема САР, описанной уравнениями (1.22)
Для рассматриваемой системы четвертого порядка
|
0 0 0 |
m1 |
|
1 |
|
c1 |
|
|
|
AH |
1 0 0 |
m2 |
; bH |
0 |
; cH |
c2 |
; dH |
d . |
|
0 1 0 |
m3 |
0 |
c3 |
||||||
|
|
|
|
|
|||||
|
0 0 1 |
m4 |
|
0 |
|
c4 |
|
|
Тогда система дифференциальных уравнений в нормальной форме:
YH1 |
m1 YH 4 |
U, |
|
|
|
YH 2 |
m2 YH 4 |
YH1 , |
|
|
|
YH3 |
m3 YH 4 |
YH 2 , |
|
|
|
YH 4 |
m4 YH 4 |
YH3 , |
|
|
|
XH |
c4 YH 4 |
c3 YH3 c2 YH 2 c1 YH1 d U. |
Если согласно приведенной системе дифференциальных уравнений в нормальной форме построить структурную схему, а затем свернуть еѐ, как это
23

выполнено в /4/, то можно выявить, из каких элементов АН, bН, сН, dН формируются коэффициенты передаточной функции вида
|
|
|
|
b |
4 |
p4 |
b |
3 |
p3 |
b |
2 |
p2 |
b p b |
0 |
|
|||
|
|
|
W(p) |
|
|
|
|
|
|
|
1 |
|
|
, |
||||
|
|
|
a |
4 |
p4 |
a |
3 |
p3 |
a |
2 |
p2 |
a |
1 |
p a |
0 |
|||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где коэффициенты числителя равны: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
b4 |
d, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b3 |
d |
m1 |
c1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
c1 |
m4 |
d m3 |
c2 , |
|
|
|
|
|
|
|
|
|
|
|
(1.24) |
||
b1 |
c2 m4 |
c1 m3 |
d m2 |
c3 , |
|
|
|
|
|
|
|
|
|
|
||||
b0 |
c3 m4 |
c2 m3 |
|
c1 m2 |
|
d m1 |
c4 , |
|
|
|
|
|
|
|
||||
и коэффициенты знаменателя: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a4 |
1, a3 |
m4 , a 2 |
|
|
m3 , a1 |
|
m2 , a 0 |
|
m1 . |
|
|
|
(1.25) |
|||||
Выражения (1.24), (1.25) и положены в основу разработанной программы PERED /5/, позволяющей получать передаточные функции по уравнениям состояния.
И подводя итоги по изложенному выше материалу о формах представления математических моделей, следует отметить, что построение моделей, основанных на системах линейных дифференциальных уравнений, записанных в форме передаточных функций, структурных схем, несмотря на большую наглядность способов представления, целесообразно при относительно невысоком порядке математических моделей. Чем выше порядок моделей, тем большие затраты времени проектировщика и ниже точность решения задач анализа и синтеза. В таком случае более приемлемой является матричная форма представления, являющаяся весьма перспективной при анализе и синтезе системы по динамическим показателям. К числу наиболее эффективных способов исследования динамики многомерных систем относятся векторно-матричные, основанные на методе переменных состояния.
В заключении следует отметить, что рассмотренные формы представления математических моделей положены в основу содержательного формализованного описания функциональных компонентов электроприводов, как объектов проектирования, в рамках инструментальных программных систем, реализующих функции моделирования либо автономно, либо в качестве соответствующих подсистем САПР.
2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ МЕХАНИЧЕСКИХ СИСТЕМ ЭЛЕКТРОПРИВОДОВ
Одним из основных универсальных уравнений, позволяющих получить математическую модель, определяющую динамические характеристики механических систем, является уравнение Лагранжа.
24
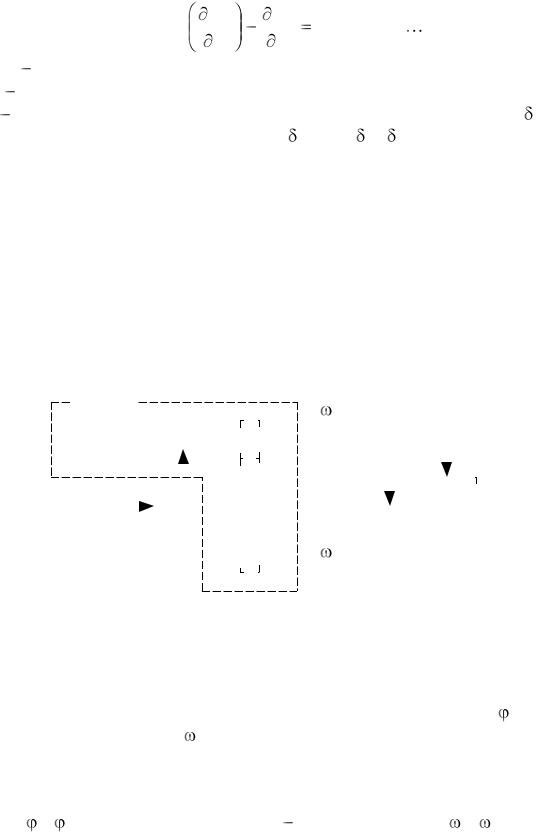
d |
|
Wk |
|
Wk |
Qi |
, (i=1,2,3 n), |
(2.1) |
dt |
|
qi |
|
qi |
|||
|
|
|
|
|
обобщенные координаты и обобщенные скорости; кинетическая энергия системы;
обобщенная сила, определяемая суммой элементарных работ Аi всех внешних сил на возможном перемещении gi, Qi = Аi/ gi.
Напомним, что к обобщенным координатам относятся физические величины, линейные или угловые перемещения, которые однозначно определяют состояние механической системы. Число обобщенных координат соответствует числу степеней свободы механической системы.
2.1.Математическая модель механической части электропривода
вабсолютных единицах
В качестве примера рассмотрим двухмассовую механическую часть электропривода (рис.2.1), для которой составим математическую модель.
J1
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MC |
|||||||||||||
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mf2 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ip |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ИМ |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
M1 |
|
Mf1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.1. Кинематическая схема с упругим звеном первого рода
На рис.2.1 отдельные массы с моментами инерции J1, J2 соединены упругими кинематическими связями С12. Для вращающейся (ротационной) системы в качестве обобщенных координат выбираем угловые перемещения i, а в качестве обобщенных скоростей i число степеней свободы равно числу обобщенных координат L=2.
Все параметры расчетной схемы приведены к валу двигателя рис.2.2.
В расчетной схеме обобщенные координаты представляют угловые перемещения 1, 2, а обобщенные скорости угловые скорости 1, 2, соответственно первой и второй масс с моментами инерции J1 и J2.
25

12
|
|
|
|
|
J1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
J2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
C12 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M12сум |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mf1 |
|
|
|
|
|
|
|
|
|
Mf2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M12сум |
|
|
|
|
|
|
|
|
|
|
|
|
|
MС |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.2.2. Расчетная схема двухмассовой последовательной упругой меха-
нической части электропривода: |
|
|
|
М1 внешний момент, создаваемый электродвигателем; М12 момент, |
|||
возникающий в упругих передачах; Мс |
момент сопротивления; Мf1, Мf2 |
мо- |
|
менты от сил внешнего вязкого трения на первой и второй массах |
|
||
Кинетическая энергия механической системы |
|
|
|
Wk=J1 12/2+J2 22/2. |
|
(2.2) |
|
Для определения обобщенной силы Q1, вычислим элементарную работу |
|||
всех приложенных к первой массе J1 моментов на возможном перемещении |
1: |
||
А1=(М Мf1 М12 сум) |
1. |
|
|
Тогда обобщенная сила, приложенная к первой массе, составит |
|
||
Q1= A1/ |
1=M1 М12 сум |
Мf1. |
(2.3) |
Аналогично для второй массы обобщенная сила |
|
|
|
Q1=М12 сум Мс Мf1. |
|
(2.4) |
|
Моменты от сил внешнего вязкого трения на первой и второй массах в |
|||
первом приближении могут быть приняты пропорционально скоростям соответствующих масс
Мf1=а1 1; Мf2=а2 2,
где а1,а2 коэффициенты внешнего вязкого трения.
Момент Мjk, возникающий в упругих элементах (передачах), определяется упругим сопротивлением:
26

t |
|
M jk C jk j k C jk ( j k )dt, |
(2.5) |
0 |
|
для нашего случая момент упругой деформации равен
M12 C12 1  2 .
2 .
Демпфирование колебаний осуществляется в материале упругой связи за счет сил внутреннего трения, пропорциональных разности скоростей первой и второй масс ω1 и ω2. В общем виде можно записать, что момент вязкого трения Mjk вт равен
|
M jk вт |
jk |
1 |
2 , |
(2.6) |
где βjk коэффициент внутреннего вязкого трения. |
|
|
|||
Для нашего случая получаем уравнение |
|
|
|
||
M12 вт |
12 1 |
2 |
вт |
1 |
2 . |
С учетом сделанных замечаний получим систему дифференциальных уравнений (2.7), подставив в уравнение Лагранжа (2.1) кинетическую энергию (2.2) и составляющие вектора обобщенных сил (2.3) и (2.4):
J1 |
d 1 |
/ dt |
M1 |
M12 |
Mf 1 M12,вт |
M1 |
C12 |
1 2 |
|||
a1 |
1 |
12 |
1 |
|
2 |
; |
|
|
|
(2.7) |
|
J2 |
d |
2 / dt |
M12 |
M12,вт Mf 2 Mс |
C12 |
|
|||||
1 |
2 |
||||||||||
|
12 |
|
1 |
2 |
а 2 |
|
2 |
Мс . |
|
|
|
Применив преобразование Лапласа к системе (2.7), мы сможем записать в операторной форме при нулевых начальных условиях систему уравнений (2.8).
1 p |
|
[(M1 |
p |
C12 / p |
1 |
p |
2 |
p |
12 1 |
p |
2 p |
||
a1 |
1 |
p )]/(J1p), |
|
|
|
|
|
|
|
|
|||
2 p |
|
[(C12 / p |
1 |
p |
2 |
p |
12 |
1 p |
2 |
p |
|
||
a2 |
2 p |
Mc |
p )]/(J2 p), |
|
|
|
|
|
(2.8) |
||||
M12 |
|
C12 / p |
1 p |
2 p , |
|
|
|
|
|
||||
M12 вт |
|
12 |
1 |
p |
2 p |
, |
|
|
|
|
|
|
|
M12 ,сум |
M12 |
M12 вт . |
|
|
|
|
|
|
|
||||
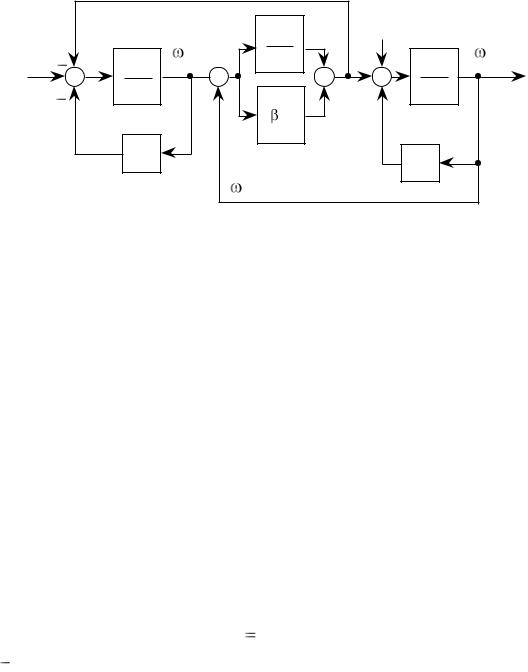
Данная система уравнений позволяет построить структурную схему двухмассовой механической части электропривода с упругим звеном первого рода, которая приведена на рис.2.3.
27
M |
|
|
C12 |
M12 |
MC(P) |
|
|
12сум |
|
|
|
|
– |
|
|
|
|
1(P) |
P |
+ |
2(P) |
||
M1(P) |
1 |
1 |
|||||
|
|
|
|||||
Mf1(P) |
J1*P |
|
|
+ |
J2P |
|
|
|
– |
|
– |
|
|||
|
|
12 |
|
|
|||
|
|
|
|
MC(P) |
|
||
|
|
|
|
M12 вт |
|
||
|
a1 |
|
|
a2 |
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
|
|
|
2(P) |
|
|
|
|
Рис.2.3. Структурная схема с упругим звеном первого рода |
|||||||
При исследовании систем электропривода целесообразно использовать метод направленного нормирования структурных моделей, разработанный Ю.А. Борцовым /6/.
2.2. Методика направленного нормирования структурных схем
Направленное нормирование исходной структурной схемы обеспечивает переход к остальным единицам непосредственно по структурной схеме в абсолютных единицах, при котором заранее планируется сохранить безразмерные коэффициенты передачи определенных звеньев равными абсолютным значениям коэффициентов передачи этих звеньев, с одновременным приведением максимально возможного количества из оставшихся коэффициентов (по выбору) к единице. Переход к системе относительных единиц связан с заменой всех переменных исходной структурной схемы произведениями их относительных значений на соответствующие базовые значения, что для звена Yi=KiXi означает
|
Yi Yiб |
Ki Xi Yiб , |
(2.9) |
|
|
|
|
где Yi |
, Xi выходная и входная переменные в относительных единицах. |
|
|
|
|
|
|
Выбор базовых величин Yiб , Xiб обычно начинают с выходной перемен-
ной автоматической системы, за базовое значение которой принимают либо номинальное значение, либо значение в наиболее характерном установившемся режиме. Дальнейший выбор базовых значений для каждого звена осуществляется непосредственно по структурной схеме с учетом особенностей его нормирования, тo есть сформулированных исследователем требований к значению коэффициента передачи звена в безразмерной структурной схеме. Так, если для i-го звена в безразмерной структурной схеме необходимо иметь некоторый
28

нормированный коэффициент передачи Ki и, следовательно: Yi Ki Xi , то,
подставляя это равенство в (2.9), получим основное соотношение, определяющее направленный выбор базовых значений математической структурной модели
|
|
|
Xiб |
|
|
(2.10) |
Действительно, Yi Yiб |
|
Ki / Ki Yiб . |
||||
Ki Xi Xiб , тогда получим, что |
|
|||||
|
|
|
|
|
|
|
|
|
|
Ki Xi Yiб |
Ki Xi Xiб , |
|
|
|
|
|
|
|
|
|
следовательно, Xiб |
Yiб Ki / Ki |
, где Ki |
Yi |
/ Xi . |
|
|
|
|
|
|
|
|
|
Таким образом, базовое значение входной величины звена равно базовому значению выходной переменной, умноженному на отношение нормирован-
ного коэффициента передачи Ki к коэффициенту передачи звена в абсолютных
единицах Кi. Это выражение (2.10) носит общий характер и отвечает всем случаям нормирования структурных схем. В частном случае, если необходимо сохранить нормированный коэффициент по значению, равным исходному коэф-
фициенту передачи структурной схемы, то есть Ki Ki , необходимо выбирать Xiб Yiб . Если же нормирование звена необходимо выполнить с приведением
коэффициента передачи звена к единице, то есть Ki |
1, то выбирают |
|
|
Xiб Yiб / Ki . |
(2.11) |
Нормирование сумматоров целесообразно осуществлять таким образом, чтобы базовые значения всех подходящих сигналов, включая сигналы обратных связей, были равны друг другу:
X1б X1б X1о.с.б. X2о.с.б. Xб , (2.12)
такой подход обеспечивает минимально возможное число коэффициентов в безразмерной структурной схеме.
Для всех звеньев структурной схемы, у которых базовые значения выходной и входной переменных окажутся уже ранее выбранными и, следовательно, заданными принудительно, переход к относительным единицам производится путем определения значения зависимого коэффициента передачи по
формуле |
(2.13) |
Ki Ki Xiб / Yiб . |
|
|
|
Последовательное применение приведенных выше формул к любой многоконтурной системе, включающей в себя замкнутые контуры и параллельные соединения, каждый из которых состоит из двух и более параллельных ветвей, позволяет сформулировать два общих правила расчета всех коэффициентов структурной схемы.
1. Коэффициент передачи любой направленной последовательности звеньев (прямого пути) в безразмерной структурной схеме K пр должен быть равен соответствующему коэффициенту структурной схемы в абсолютных еди-
29
ницах Kпр , умноженному на отношение базовой величины его входной переменной данного пути Xвх.б. к базовой величине его выходной Xвых .б. .
|
Kпр Xвх.б. / Yвых .б. |
Kпр |
2. Коэффициенты передачи всех контуров после перехода к безразмерной структурной схеме сохраняют свое прежнее значение: K K .
Число зависимо нормируемых коэффициентов Nзн структурной схемы, то есть коэффициентов, значения которых нельзя выбирать произвольно и кото-
рые находятся по формуле (2.13), определяются выражением |
|
Nзн=А В+С, |
(2.14) |
где А число параллельных ветвей во всех параллельных соединениях нормируемой схемы; В число независимых параллельных соединений этой нормируемой схемы; С число замкнутых контуров в ней.
Зависимые нормируемые коэффициенты передачи для звеньев замкнутых контуров Kзк согласно второму правилу оказываются равными реальному коэффициенту передачи контура К, деленному на произведение коэффициентов
передачи остальных звеньев контура |
(2.15) |
Kзк K /(K1к K2к ) . |
|
|
|
Это выражение (2.15) целесообразно использовать при проверке правильности определения нормированных коэффициентов в контуре. Поскольку полное число коэффициентов N в схеме известно, то число свободно нормируемых коэффициентов можно определить по формуле:
Nсв=N Nзн.
Применим рассмотренную методику к нормированию структурной схемы двухмассовой механической части с упругим звеном первого порядка, представленной на рис.2.3. Для указанной схемы (рис.2.3) число независимых параллельных соединений В=1, число параллельных ветвей А=2, число замкнутых контуров С=4. Следовательно, в соответствии с формулой (2.13) число зависимых коэффициентов равно:
Nзн=А В+С=2 1+4=5 при общем числе звеньев, равном 6. Таким образом, лишь один коэффициент может быть выбран произвольно.
Выберем базовые значения моментов:
М1.б.=Мс.б.=М12.б.=Мf1.б.=Мб.=Xб..
И угловой скорости:
1.б= 2.б.= б.=Yб..
Тогда в соответствии с формулой (2.13) отношение 1/(J1p) можно записать в виде нормированного коэффициента передачи:
|
|
Mб |
|
1 Mб |
1 |
|
|||
K1 |
К |
|
|
|
|
|
|
|
, |
Wб |
|
J1 Wб |
|
TM1 |
|||||
|
|
|
|
|
|||||
30
