
Учебное пособие 1499
.pdf
Из математических моделей элементов формируются математические модели систем, в которые, наряду с компонентными уравнениями, обязательно входят уравнения, отражающие способ связи элементов между собой в составе системы, называемые топологическими. Их особенностью является то, что каждое из них связывает однотипные фазовые переменные, относящиеся к разным элементам системы. Примером могут служить уравнения законов Кирхгофа. С ростом числа элементов растет порядок системы уравнений, соответственно растут затраты машинного времени на ее решение. Возможности моделей макроуровня оказываются исчерпанными и возникает необходимость перехода к модели третьего уровня.
На метауровне для моделирования аналоговой системы широко применяют аппарат анализа системы автоматического управления, а для моделирования цифровой системы математическую логику, теорию массового обслуживания. На метауровне с помощью дальнейшего абстрагирования от характера физических процессов удается получить приемлемое по сложности описание информационных процессов, протекающих в объектах. Поэтому модели этого уровня называют еще информационными.
На информационном уровне в качестве объектов рассматриваются, например, сложные устройства и комплексы вычислительной техники, системы управления, электрические системы. Дискретность представления пространства и времени обусловливается дискретностью фазовых переменных, которыми являются величины, характеризующие состояние элементов. Роль элементов и внутренних параметров выполняют системы и выходные параметры предыдущего иерархического уровня. Иными словами, можно сказать, что математические модели этого уровня включают в себя в качестве элементов модели объектов макроуровня, внешние параметры которых становятся внутренними. На информационном уровне функционирование системы представляет последовательность событий, происходящих в дискретные моменты времени, каждое из которых заключается в изменении состояния какого-либо элемента системы: "занято" и "свободно", то есть фазовые переменные на этом уровне рассматриваются двоичными.
Математические модели на метауровне – это системы обыкновенных дифференциальных уравнений, системы логических уравнений, имитационные модели систем массового обслуживания.. Кроме того, на основе алгебры логики создаются математические модели многих устройств при решении задач их структурного синтеза. Сам методологический прием получения математической модели с применением раздела математической логики – алгебры логики или булевой алгебры – называется логическим моделированием. В алгебре логики изучаются отношения между дискретными двузначными величинами, которые могут принимать одно из двух возможных значений. Эти возможные значения обозначают цифрами 1 и 0 или соответственно словами "истина" и
11

"ложь". Подобные величины и операции над ними называют булевыми переменными и булевыми (логическими) операциями.
Отношения между булевыми переменными выражаются булевыми функциями, которые могут принимать значения 1 и 0. К числу основных булевых функций относят конъюнкцию (последовательное соединение, умножение) – символ /\, дизъюнкцию (параллельное соединение, сложение) – символ \/ и отрицание – символ " " над одним из аргументов (в этом случае функция Y принимает всегда противоположное значение аргументу, то есть Y=1 при x=0 и
Y=0 при x=1).
1.2. Требования, предъявляемые к математическим моделям
Основными требованиями, предъявляемыми к математическим моделям, являются требования точности (адекватности), универсальности (массовости) и экономичности.
Адекватность. Модель считается адекватной, если отражает заданные свойства объекта с приемлемой точностью. Точность математической модели определяется степенью совпадения предсказанных или рассчитанных с ее по-
мощью значений параметров объекта с реальными значениями. Пусть |
j – отно- |
сительная погрешность модели по j-му выходному параметру |
|
j = ( YMj – Yj ) / Yj , |
(1.4) |
где YМj – j-й выходной параметр, рассчитанный с помощью модели; Yj – тот же выходной параметр, имеющий место в моделируемом объекте.
Требование универсальности математической модели предполагает возможность ее применения для описания объектов достаточно широкого класса и для анализа всех или многих режимов их функционирования.
Экономичность математической модели может оцениваться прежде всего затратами машинного времени Tмаш, которое для обеспечения независимости от типа ЭВМ выражают числом элементарных операций, выполняемых при однократном решении уравнений модели. Показанием экономичности математической модели может служить также число внутренних параметров, используемых в ней. Чем больше таких параметров, тем больше затраты машинной памяти, тем больше усилий требуется для получения сведений о числовых значениях параметров и их разбросе. Требование высокой точности, большой степени универсальности, с одной стороны, и высокой экономичности с другой, противоречивы.. Поэтому необходим удачный компромисс.
И подводя итоги изложенному, дополним некоторые определения и дадим классификацию математических моделей объектов.
1.3. Классификация математических моделей
12

Математическая модель технической системы (объекта), полученная непосредственным объединением моделей элементов в общую систему уравнений, называется полной математической моделью.
Математическую модель, более простую по сравнению с полной, с точки зрения затрат машинного времени и памяти при ее использовании, называют еще макромоделью. Эта модель есть аппроксимация полной модели. Как правило, она уже не отражает внутреннюю структуру объекта, поскольку в модели не фигурируют внутренние фазовые переменные. Макромодель представляет собой совокупность соотношений, связывающих только входные и выходные фазовые переменные (возможно, также и их производные).
По характеру переменных, фигурирующих в модели, различают модели фазовые и факторные. Фазовыми моделями называются такие модели, в которых фигурируют фазовые переменные. Факторная модель – это математическая модель вида
F1 ( V, X ) = 0 , |
(1.5) |
где V вектор внешних параметров, X вектор выходных параметров.
В большинстве случаев факторные модели удается получить в явной
форме |
|
X = F2 ( V ). |
(1.6) |
В зависимости от мощности множества значений переменных различают непрерывные математические модели в случае непрерывной совокупности, то есть при континуальном множестве значений дискретные математические модели имеют место при конечном или счетном множестве значений переменных.
Функциональные модели по способу получения делят на теоретические и формальные (или экспериментальные).
Теоретическая модель строится в процессе изучения физических закономерностей, проявляющихся в объекте, они являются продуктом теории объектов данного класса, поэтому и параметры такой модели имеют вполне определенный физический смысл.
Формальные модели получают на основе экспериментов с объектом, в ходе которых изучаются зависимости выходных переменных объекта от входных без рассмотрения внутренних механизмов функционирования объекта (метод "черного ящика").
Различают также: динамические модели, которые учитывают инерционность процессов в объекте, и статические модели, не учитывающие эти факторы. В зависимости от линейности или нелинейности уравнений различают соответственно линейные и нелинейные математические модели. Модели, в которых искомые переменные явно выражены через известные величины, называют аналитическими моделями. Аналитические модели имеют вид явных зависимостей одних параметров объекта от других и от параметров окружающей среды.
13
В отличие от них в алгоритмических моделях вычисление значений искомых величин связано с необходимостью решения систем уравнений.
Алгоритмические модели в системе уравнений учитывают форму задания связей между параметрами окружающей среды, выходными и внутренними параметрами объекта. Среди алгоритмических моделей важный класс составляют имитационные модели, предназначенные для имитации физических или информационных процессов в объекте при задании различных зависимостей входных воздействий от времени, то есть переменные в моделях рассматриваются как функции времени. Собственно имитацию независимых процессов определяют как имитационное моделирование. Результат имитационного моделирования – зависимости фазовых переменных в избранных элементах системы от времени.
Используются достаточно широко специальные модели, ориентированные на определенные задачи обработки и отображения информации. Например, модели геометрии объектов, используемые в подсистемах отображения графической информации, документирования.
1.4. Формы представления математических моделей
Процесс проектирования, как известно, представляет собой многократный поиск оптимальной структуры и параметров разрабатываемого объекта. Поэтому небезразлично, какие формы представления математической модели приняты в условиях автоматизированного проектирования, предполагающем постоянное и эффективное применение ЭВМ.
Построение моделей, основанных на системах линейных дифференциальных уравнений, записанных в форме передаточных функций, позволяют проектировщику выявить все внутренние связи, определить возможные места включения компенсационных устройств. Данный способ представления объектов особенно часто применяют при частотных исследованиях систем регулирования, однако, несмотря на большую наглядность, им удобно пользоваться лишь при относительно невысоком порядке математической модели, так как не требуется значительных затрат времени проектировщика, ЭВМ, но не всегда обеспечивается необходимая точность решения задач анализа и синтеза автоматизированного электропривода.
Использование графов позволяет найти пути прохождения сигналов через элементы объекта, определить сильные и слабые связи и упростить структуры объектов за счет исключения слабых связей, что приводит к уменьшению порядка уравнений, описывающих динамику автоматизированного электропривода, и, таким образом, к сокращению объема проводимых вычислительных работ.
14

Эффективность еще более повышается с применением метода переменных состояния, где используются уравнения первого порядка. Для решения на ЭВМ систему этих уравнений записывают в векторно-матричной форме, что дает возможность представить модель в компактной и унифицированной форме для широкого класса объектов. К ним относятся непрерывные, дискретные и дискретно-непрерывные стационарные и нестационарные системы линейного типа, а также некоторые нелинейные системы. В системах такого рода с помощью методов теории пространства состояний и спектрального разложения матриц удается получить ее дискретную модель в форме, удобной для реализации на ЭВМ. Главное преимущество матричной формы записи заключается в том, что, составляя матрицы по определенным правилам, можно трансформировать в матричную форму не только запись переменных, но и операции над ними.
Математическое обеспечение современных ЭВМ программами, ориентированными на унифицированное матричное представление задач анализа и синтеза многомерных систем, дает возможность для этих целей использовать современную вычислительную технику /1/. В пользу рассматриваемой формы представления свидетельствует и то, что матрицы позволяют получить структурные схемы или графы. Впрочем, можно сделать и обратное преобразование. Рассмотрим в связи с этим несколько подробнее метод переменных состояния. Под переменными состояния понимается минимальный набор физических параметров, которые позволяют полностью описать поведение системы, если известны их начальные и внешние воздействия /3/. Динамика подобных систем описывается системой уравнений первого порядка относительно переменных состояния. При такой форме записи эти переменные аналогичны обобщенным координатам, а пространство их изменения является фазовым. Состояние элемента в любой текущий момент времени характеризуется совокупностью фазовых координат, которые можно объединить в вектор состояния и представить их описание в векторной форме (математической моделью) /4/.
1.4.1. Метод переменных состояния
Обычно при описании элементов непрерывного действия с использованием переменных состояния Y(t) и связанных с ними выходных X(t) и входных U(t) переменных применяют следующие уравнения:
Y(t) |
f (Y(t),U(t),t) , |
(1.7) |
|
|
|
X( t) |
q(Y(t),U(t),t) |
|
где
15
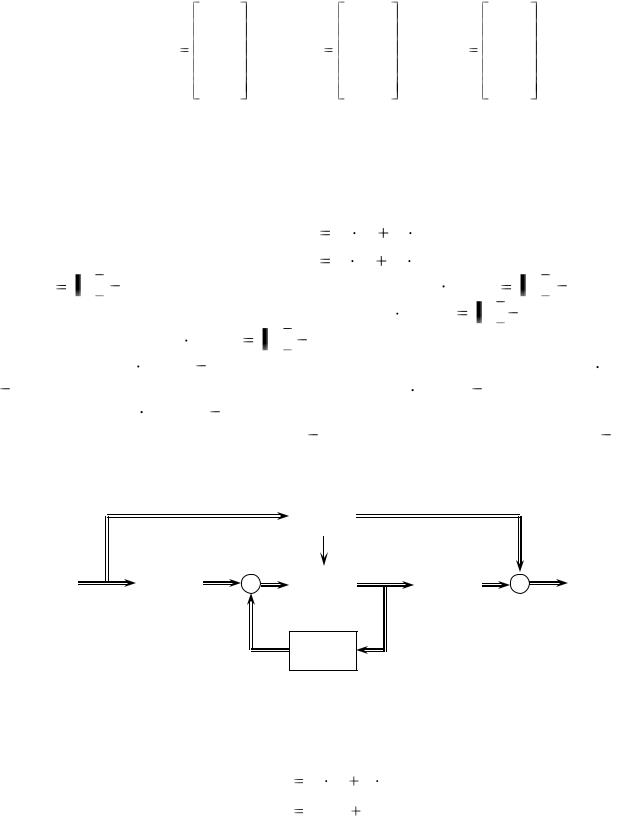
Y1(t) |
|
U1(t) |
X1(t) |
|
|
Y2 |
(t) |
U(t) |
U2 (t) |
X2 (t) |
. |
Y(t) |
; |
; X(t) |
|
||
: |
|
|
: |
: |
|
Yn (t) |
|
Um (t) |
Xr (t) |
|
|
Уравнения (1.7) справедливы на интервале времени ( t0,t ) при заданных начальных условияхY0 (t),U0 (t) . Остановимся на случае, когда уравнения, со-
ставляющие систему (1.7) – линейные и стационарные, поэтому входящие в уравнения коэффициенты не зависят от времени. В векторно-матричной форме
эти уравнения описывают свойства динамического элемента системы: |
|
|
|||||||
|
|
|
Y |
A Y |
B U; |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.8) |
|
|
|
X |
C Y |
D U, |
|
|
|
|
|
|
|
|
|
|
|
|||
где A aij |
системная матрица размерностью ( n n ); |
B |
bij |
матрица |
|||||
управления (входная матрица) размерностью ( n m ); C |
cij |
выходная мат- |
|||||||
рица размерностью ( r n ); D dij |
матрица сквозной передачи управления |
||||||||
размерностью ( r m ); X |
вектор выходных переменных размерностью ( l |
r ); Y |
|||||||
вектор переменных состояния размерностью ( l n ); U |
вектор управления |
||||||||
размерностью ( l m ); n |
количество переменных состояния, |
характеризует |
|||||||
порядок многомерности системы; m |
|
количество входов управления; r |
ко- |
||||||
личество выходов. Структурная схема линейных многомерных систем автоматического регулирования (САР) приведена на рис.1.5.
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y (t) |
Y(0) |
|
|
|
|||
|
|
|
|
|
|
|
|
+ |
||
|
|
|
|
|
|
|
|
Y(t) |
|
|
|
B |
|
|
|
|
1/p |
|
C |
|
|
U(t) |
|
|
|
|
|
|
X(t) |
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||
A
Рис.1.5. Структурная схема линейных многомерных САР
Если элемент имеет один вход и один выход, уравнения состояния записываются в виде:
Y A Y b U;
(1.9)
X cт  Y d
Y d  U,
U,
16
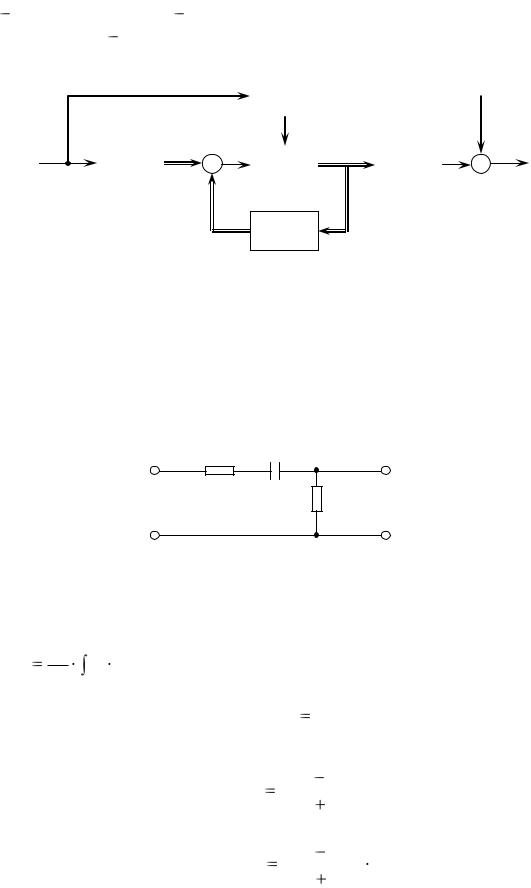
где b входной вектор; cт выходной вектор, транспонированный по отношению к вектору c; d коэффициент сквозной передачи управления. Структурная схема линейных одномерных САР представлена на рис.1.6. Уравнения (1.8) и
|
|
Y (t) |
d |
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
Y(0) |
|
|
|
|
||||
|
|
|
|
|
|
|
+ |
|||
|
b |
|
|
|
1/p |
|
Y(t) |
cт |
||
|
|
|
|
|
|
|
||||
U(t) |
|
|
|
|
|
|
X(t) |
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
|
|||||||
A
Рис.1.6. Структурная схема линейной одномерной САР
(1.9) являются уравнениями состояния элемента или целой системы автоматического регулирования и применяются при математическом моделировании динамических элементов, результатом которого являются соответствующие переходные процессы.
Применение векторно-матричной формы представления элементов автоматизированного электропривода покажем на некоторых примерах.
Пример 1. Для корректирующего устройства (рис.1.7) составим уравне-
R1 |
C |
|
R2 |
U2 |
|
||||
U1 |
|
|
Рис.1.7. Схема корректирующего звена
ния переменных состояния. В качестве переменной состояния можно взять напряжение на конденсаторе C1 .
Напряжение на конденсаторе определяется по формуле
1
UC C1 iC dt ;
dUC |
|
iC |
. |
(1.10) |
|
|
|||
dt |
|
C1 |
|
|
Ток, протекающий через конденсатор, равен
iC |
(U1 |
U C ) |
. |
(1.11) |
|
|
|||
|
(R1 |
R 2 ) |
|
|
Представив его значение в уравнение (1.10), получим выражение
dUC |
|
(U1 |
UC ) |
C1 . |
(1.12) |
dt |
|
(R1 |
R 2 ) |
||
|
|
|
17

Тогда напряжение U2 на выходе определяется уравнением |
|
|||
U 2 |
(U1 |
U C ) R 2 |
. |
(1.13) |
|
|
|||
|
R1 |
R 2 |
|
|
В векторно-матричной форме уравнения (1.12) и (1.13) записываются для элемента, имеющего один вход и выход, системой уравнений (1.9)
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
U1 |
, |
|||
|
|
UC |
|
R1 C1 |
R |
2 C1 |
UC |
|
R1 C1 |
|
R 2 C1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
U2 |
|
|
R 2 |
UC |
|
|
|
R 2 |
|
U1 , |
|
(1.14) |
||||
|
|
|
|
|
|
|
R1 |
R 2 |
|
|
R1 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R 2 |
|
|
||||||||
где |
A |
|
|
1 |
|
|
; |
|
b |
|
|
|
1 |
|
|
|
; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
R1 |
C1 R 2 |
C1 |
|
R1 C1 |
R 2 C1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
c |
T |
|
R 2 |
|
; |
|
|
|
d |
|
|
R 2 |
. |
|
|
|
|
||||
|
|
|
R1 |
|
R 2 |
|
|
|
R1 |
R 2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Системе уравнений (1.14) соответствует структурная схема корректирующего устройства, изображенная на рис.1.7, свернув которую и подставив
значения A, b, cт , d , получим хорошо известную передаточную функцию /4/
W(p) |
U2 (p) |
|
T2 (p) |
, |
U1 (p) |
1 T1 (p) |
|||
где T1 C1 (R1 R 2 ) ; T2 C1 R 2 . |
|
|
|
|
Как видно из структурных схем (рис.1.5, 1.6, 1.8), коэффициент d и матрица D сквозной передачи управления появляются при наличии в системе параллельно включенных звеньев.
18

|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
+ |
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
b |
|
UC |
1/p |
UC |
cт |
|
|
|
U1 |
|
|
|
|
U2 |
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
||||||
A
Рис.1.8. Структурная схема корректирующего звена
Из примера следует, что существует полное совпадение между описанием объекта как с помощью уравнений переменных состояния, так и передаточных функций.
Как уже указывалось выше, для удобства анализа систем автоматического регулирования на вычислительной технике следует представить эту систему в векторно-матричной форме. Но часто бывает, когда объект уже описан передаточной функцией. В таком случае нет необходимости описывать его заново через переменные состояния, можно просто преобразовать передаточную функцию в уравнения состояния. Пусть дана передаточная функция первого порядка вида
W(p) |
b1 |
p |
b0 |
. |
(1.15) |
|
|
|
|||
|
a1 |
p |
a 0 |
|
|
Структурная схема, соответствующая ей, представлена на рис.1.9.
|
|
|
|
|
b1 |
|
|
|
U |
|
|
Y |
|
|
+ |
||
|
|
|
|
|
||||
|
|
|
Y |
|
||||
|
1/a1 |
1/p |
b0 |
|||||
|
|
|
||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
X |
|
Y |
|
|
|
|
|||
|
|
|
|
|
|
|
||
a0
Рис.1.9. Общая структурная схема для звена первого порядка
Согласно приведенной структурной схеме (рис.1.9) запишем уравнения переменных состояния:
|
Y a 0 |
|
U |
|
Y |
a1 |
|
a1 |
, |
19
X |
b0 a 0 b1 |
|
U b1 |
a1 |
|
a1 |
|
|
|
и определим значения коэффициентов согласно уравнениям (1.9)
A |
a 0 |
; b |
1 |
; c |
b0 b1 a 0 |
; d |
b1 |
. |
|
|
|
|
|||||
|
a1 |
a1 |
a1 |
a1 |
||||
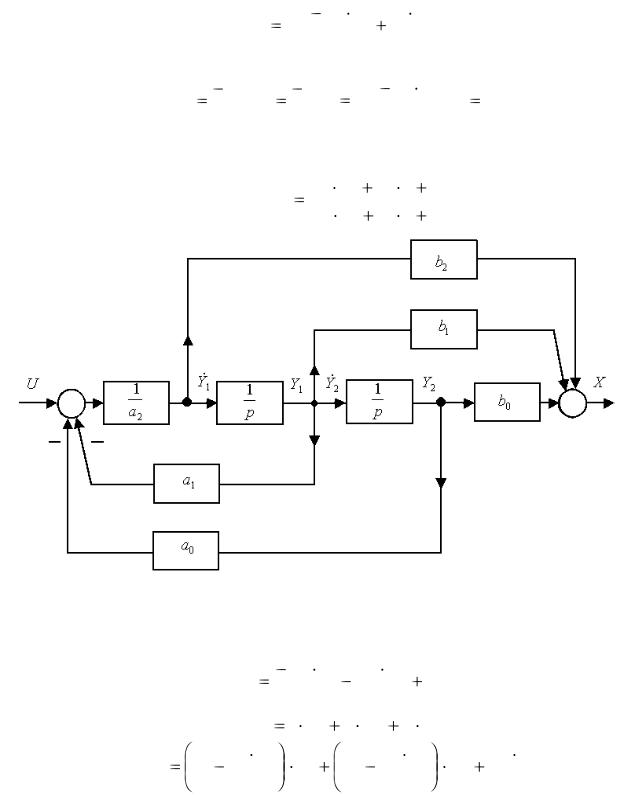
Для передаточной функции второго порядка, структурная схема которой изображена на рис.1.10, можно проделать те же процедуры
|
b |
2 |
p2 |
b |
p |
b |
0 |
|
|
W(p) |
|
|
1 |
|
|
. |
(1.16) |
||
|
|
p2 |
|
|
|
|
|||
|
a 2 |
a1 |
p |
a 0 |
|
||||
Рис.1.10. Общая структурная схема для звена второго порядка
Согласно структурной схеме (рис.1.10) запишем уравнения состояния
|
|
|
|
Y1 a1 |
|
Y2 |
a 0 |
|
|
U |
|
|
|
|
|
|
|
Y1 |
|
|
a 2 |
|
a 2 |
a 2 |
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
Y2 1 Y1 |
0 Y2 |
0 U, |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X b1 |
a1 |
b2 |
|
Y1 |
b0 |
a0 b2 |
|
|
Y2 |
b2 |
U |
. |
(1.17) |
|||
a |
2 |
|
|
a 2 |
|
|
a 2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда коэффициенты компактной формы записи (1.9) будут равны
20
