Учебное пособие 1498

Проведем касательную к кривой y = f(x) в этой точке. Уравнение касательной имеет вид:

Из неравенства y ~y 0 следует, что кривая у = f(x) лежит ниже касательной, а, значит, она выпукла.

Аналогично доказывается, что если f (x) > 0 в интервале (a, b), то кривая y = f(x) вогнута в интервале (a, b).

Пример. Определить направление выпуклости кривой y(x) ln x с помощью второй производной.

Решение. Вычислим вторую производную:

Следовательно, логарифмическая функция по основанию е везде на области определения выпуклая.

Определение 7.6. Точка, отделяющая выпуклую часть кривой от вогнутой части, называется точкой перегиба.

Очевидно, что в точке перегиба кривая пересекает касательную, на рис. 19 это точка L.

Теорема 7.6. Пусть вторая производная f (a) = 0 или f (a) не существует. Если при переходе через точку х = а меняет знак f (x), то точка кривой с абсциссой х = а является точкой перегиба.

Доказательство.

Пусть f (x) < 0 при х < a и f (x) > 0 при x > a. Тогда при x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба.

61

Пусть f (x) > 0 при x < a и f (x) < 0 при x < a. Тогда при x < a кривая обращена выпуклостью вниз, а при x > a – выпуклостью вверх. Тогда x = a – точка перегиба.

Замечание. Отметим, что ситуация применения первой производной для нахождения точек экстремума полностью аналогична ситуации со второй производной для нахождения точек перегиба (единственное отличие, что по определению точки экстремума лежат на числовой оси Оx, а точки перегиба на графике функции). Поэтому в обоих случаях сначала применяют необходимые условия и находят нули соответствующих производных, потом, расставив знаки производных, проверяют достаточные условие для полученных точек.

Пример.

1. Исследовать кубическую параболу y(x) x3 /3 2x2 3x 1 с помощью первой и второй производных.

2. Определить количество корней уравнения x3 /3 2x2 3x 1= 0. Решение.

1. Исследуем функцию по первой производной:

у' = (х3/3–2х2+3х+1)' = х2–4х+3 = 0.

По теореме Виета х1 = 1, х2 = 3. Расставим знаки производной (в нашем случае для параболы, ветви которой идут вверх), график производной этой функции указан на рис. 20.

Следовательно, исследуемая кубическая парабола убывает при х (1,3) и возрастает при х (–∞,1) (3,+ ∞), тогда

Рис. 20. График производной функции y(x) x3 /3 2x2 3x 1

Исследуем функцию по второй производной:

у'' = (х2–4х+3)'=2х–4=0,

62

Построим схематический график кубической параболы, что указано на рис. 21.

Рис. 21. График функции кубической параболы y(x) x3 /3 2x2 3x 1

2. Определим количество корней уравнения.

Так как т. А2 лежит выше оси Оx (см. рис. 21), то уравнение x3 /3 2x2 3x 1 0 (его левая часть будет F(x) = 3f(х)) имеет единственное решение.

Можно еще вычислить значения левой части уравнения F(x) =

х3–6х2+9х+3 в двух целочисленных точках F(0) = 3, F(–1) = –1–6–9+3 = –13. Так как они разных знаков, то по теореме о промежуточных значениях непрерывной функции у кубического уравнения будет ко-

рень х1 (–1, 0).

Если нам надо будет повысить точность (например, до 0.1), то вычислим значение функции F(x) при х = – 0.4 (обычно берут середину отрезка, но из поведения функции на интересующем нас промежутке (см. рис. 20) следует, что корень лежит ближе к правому кон-

цу): F(–0,4) = –0.064–6·0.16–3.6+3 < 0, поэтому выберем интервал (– 0.4;0), на концах которого значения функции будут опять разных знаков и, следовательно, корень находится в этом интервале, возьмем на этот раз середину х = – 0,2. Наконец, F(–0,2) = –0.008–0.24– 0.18+3=2.572 > 0 и, взяв середину интервала (–0.4; –0.2) длиной 0.2,

найдем х = – 0.3; в результате мы и получим ответ с заданной точностью 0.1.

63

7.4. Асимптоты

При исследовании функций часто бывает, что при стремлении аргумента функции x x0 , где x0 или x0 , сама кривая неограниченно приближается к некоторой прямой.

Определение 7.7. Прямая для заданной кривой называется асимптотой, если кратчайшее расстояние от переменной точки кривой до этой прямой стремится к нулю при x x0 , где x0 конечное или бесконечное число.

Следует отметить, что не любая кривая имеет асимптоту. Асимптоты можно классифицировать. Асимптоты могут быть

вертикальные (в точках разрыва функции) и наклонные. Частным случаем наклонных асимптот являются асимптоты горизонтальные. Исследование функций на асимптотическое поведение имеет большое значение и при наличии асимптот позволяет более точно определить характер поведения функции, что упрощает построение графика.

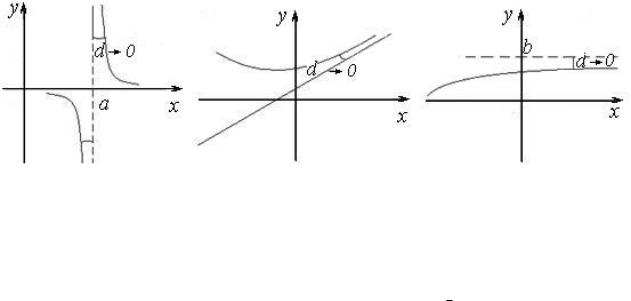
На рис. 22 указаны вертикальная, наклонная и горизонтальные асимптоты, соответственно.

Рис. 22. Различные виды асимптот [3]

Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как пока-

x

зано на рис. 23 для графика функции y x e 3 sin x. Ее наклонная асимптота у = х.

Но для подавляющего большинства функций при подходе их графика к асимптоте вторая производная знака не меняет, и кривая подходит к своей асимптоте с одной стороны. Рассмотрим подробнее методы нахождения асимптот кривых.

64

x

Рис. 23. График функции y x e 3 sin x с асимптотой

7.4.1. Вертикальные асимптоты

Из определения асимптоты следует, что если lim f (x) или

тота кривой y = f(x).

Например, для функции f (x) 2 прямая х = 5 является такой

x 5

асимптотой. Напомним, что по определению в точке х = 5 на оси Оx у данной функции будет бесконечный разрыв второго рода.

7.4.2. Наклонные асимптоты

Предположим, что кривая y = f(x) имеет наклонную асимптоту y kx b, что указано на рис. 24, где М – точка пересечения кривой и перпендикуляра к асимптоте, N – точка пересечения этого перпендикуляра с прямой.

Рис. 24. Иллюстрация наклонной асимптоты [3]

65

Замечание. Как уже было сказано, асимптоты бывают не у всех функций, как правило, это функции бесконечно растущие (убывающие) при x , но функции с асимптотами более предсказуемы.

7.5. Общая схема исследования функций

Процесс исследования функции состоит из нескольких этапов. Для наиболее полного представления о поведении функции и построения ее графика необходимо:

1.Найти область определения и область значения функции;

2.Установить четность, нечетность, периодичность функции; найти точки её пересечения с осями;

3.Определить асимптоты: вертикальные (точки разрыва функции), наклонные (в том числе горизонтальные);

4.Определить точки экстремума функции, промежутки возрастания и убывания функции;

5.Определить точки перегиба функции, промежутки выпуклости и вогнутости функции;

6.Составить таблицу по всем особым точкам функции, к которым относят все точки, в которых обращаются в ноль или не определены производные (см. п. 4 и п. 5);

7.Построить график по таблице (cначала нанести на плоскость xOy точки пересечения функции с осями, ее асимптоты и все

критические точки производных).

Пример. Исследовать функцию и построить ее график

1

y(x 2)ex .

1.Область определения: вся числовая ось за исключением точки x 0, или x , 0 0, .

2.Полезно определить точки, где график пересекает оси координат, а также учесть периодичность, четность или нечетность функции.

Внашем примере функция не является периодической, так как не содержит тригонометрических функций.

торую обозначим A(–2;0).

69

Пересечение графика с осью Oy происходит при x 0. В нашем случае это невозможно, так как x 0 не входит в область определения.

3. Изучим поведение функции на границе области определения, то есть выясним, к чему стремится y, если x приближается к границам области определения.

Рассмотрим граничную точку x 0. Определим односторонние пределы:

есть вертикальная асимптота. В нашем случае вертикальной асимптотой является прямая x 0, то есть ось Oy.

Коэффициенты k и b определены и конечны, а значит, y графика функции при x есть наклонная асимптота y x 3.

4. Исследуем функцию по первой производной:

Как известно, точки экстремума функции находятся среди тех точек области определения, в которых производная первого порядка равна нулю или не существует:

нулем являются точки x 1 и x 2;особой точкой y x является x 0.

70