Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 1491

.pdf

Скачиваний:

Добавлен:

30.04.2022

Размер:

1.24 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

117

(p)< f (q) или f / (q)>0. Если ни одно из условий не выполнено, удваиваем расстояние от p до q до тех пор пока p,q .

3.По формуле (3.15) находим *1.

4.Проверим, можно ли точку * считать точкой минимума

с точностью , то есть f / (*k+1) ,

k=0,1, ... Если условие прекращения поиска выполнено, то задача решена и *= *k+1. В противном случае продолжаем вычисления.

5. Если f / (*k+1)>0 , то выбираем вместо интервала

(p,q) интервал (p, *k+1), в противном случае – (*k+1,q), то есть тот интервал, который содержит точку минимума и переходим к пункту 3 данного алгоритма.

3.11. Задания и вопросы для самостоятельной подготовки

1В чем основная идея любого метода поиска?

2Какие условия прекращения поиска Вы знаете?

3Проведите сравнительный анализ градиентных методов и дайте рекомендации по их применению.

3Для решения каких задач используются mетоды однопараметрической оптимизации?

4Оцените эффективность метода Давидона Флетчера Пауэлла.

4.Лабораторный практикум

4.1.Лабораторная работа 1.

Оптимизация размещения модулей на коммутационном поле методом парных перестановок

4.1.1.Общие указания по выполнению лабораторной работы

118

Целью лабораторной работы является углубление и закрепление знаний по вопросам оптимизации размещения модулей на коммутационном поле (прямоугольной или какой-либо другой формы) методом парных перестановок и получение практических навыков использования ЭВМ IBM PC для решения таких задач. В процессе выполнения лабораторной работы студент должен уметь практически применять полученные знания и приобретенные навыки для:

составления исходных данных и решения на ЭВМ задач оптимального размещения модулей;

решения вопросов оптимизации размещения модулей с помощью алгоритма парных перестановок;

исследования и оценки эффективности алгоритма оптимального размещения модулей.

На выполнение лабораторной работы отводится четыре часа. Перед лабораторным занятием студент должен самостоятельно выполнить домашнее задание в соответствии с данными методическими указаниями.

Студент, явившийся на занятия, должен иметь методические указания по данной лабораторной работе, полученные в библиотеке. В начале занятия преподаватель проверяет выполнение студентом домашнего задания и наличие заготовки отчета по данной лабораторной работе в его рабочей тетради.

К выполненной работе прилагаются необходимые эскизы, схемы алгоритмов, распечатки машинных решений и другие материалы согласно указаниям по оформлению отчета. При проведении лабораторных занятий в машинном зале студенты должны предварительно

изучить инструкцию по технике безопасности по эксплуатации ЭВМ.

119

4.1.2.Домашнее задание и методические указания по его выполнению

При выполнении домашнего задания студент должен ознакомиться с алгоритмом оптимизации размещения модулей на коммутационном поле путем парных перестановок. Для этого необходимо воспользоваться учебником [I, с. 188-212]. В связи с тем, что в учебнике вопрос оптимизации размещения модулей на коммутационном поле методом парных перестановок рассматривается недостаточно подробно необходимо проработать также следующий материал.

Под оптимальным размещением обычно понимается такое местоположение модулей, при котором наилучшим образом удовлетворяются некоторые требования. В качестве модулей могут быть выбраны как отдельные радиоэлементы ( микросхемы, транзисторы, диоды, резисторы и т. д. ), так и типовые элементы замены ( ТЭЗы), блоки, панели и т. д. При этом предполагается , что модули определенным образом ( согласно электрической схемы ) соединяются между собой.

В общем случае задача оптимального размещения носит многоцелевой характер и при еѐ решении оптимизация должна проводиться по совокупности критериев качества. Учет многих критериев резко усложняет решение задачи, поэтому в каждом конкретном случае обычно выделяют наиболее важный критерий, а остальные не учитывают или используют в качестве ограничений задачи. Таким наиболее важным критерием оптимизации при размещении модулей чаще всего выбирают минимизацию суммарной длины соединений между размещаемыми модулями.

Выбор этого критерия обусловлен тем, что он обеспечивает такие положительные эффекты, как повышение надежности соединений, сни-жение паразитных емкостей и взаимосвязей,

120

снижение трудоемкости изготовления и количества используемого провода при проводном монтаже.

4.2.Лабораторная работа 2.

Минимизация числа пересечений проводников при автоматизированном размещении элементов РЭС на коммутационном поле

4.2.1. Общие указания по выполнению лабораторной работы

составления исходных данных и решения на ЭВМ задач оптимального размещения модулей;

решения вопросов оптимизации размещения модулей с помощью алгоритма парных перестановок;

исследования и оценки эффективности алгоритма оптимального размещения модулей.

Студент, явившийся на занятия, должен иметь методические указания по данной лабораторной работе, полученные в библиотеке. 121

В начале занятия преподаватель проверяет выполнение студентом домашнего задания и наличие заготовки отчета по данной лабораторной работе в его рабочей тетради.

предварительно изучить инструкцию по технике безопасности по эксплуатации ЭВМ.

4.2.2.Домашнее задание и методические указания по его выполнению

4.2.2.1. Оптимизация размещения с помощью алгоритма парных перестановок

Под оптимальным размещением обычно понимается такое ме-стоположение модулей, при котором наилучшим образом удовлетворяются некоторые требования. В качестве модулей могут быть выбраны как отдельные радиоэлементы (

микросхемы, транзисторы, диоды, резисторы и т. д. ), так и типовые элементы замены ( ТЭЗы), блоки, панели и т. д. При

122

этом предполагается , что модули определенным образом ( согласно электрической схеме ) соединяются между собой.

В общем случае задача оптимального размещения носит многоцелевой характер, и при еѐ решении оптимизация должна проводиться по совокупности критериев качества. Учет многих критериев резко усложняет решение задачи, поэтому в каждом конкретном случае обычно выделяют наиболее важный критерий, а остальные не учитывают или используют в качестве ограничений задачи. Одним из важных критериев оптимизации при размещении модулей часто выбирают минимизацию числа пересечений проводников, так как она обеспечивает такие положительные эффекты, как уменьшение числа проволочных перемы-3

чек, упрощение формы печатных проводников, что в конечном итоге ведет к снижению трудоемкости изготовления изделия, повышению надежности соединений и упрощению трассировки печатных плат.

Решение задач оптимального размещения модулей ( одинаковых или примерно одинаковых по размерам ) может быть осуществлено с помощью алгоритма парных перестановок модулей [ 1 ]. Суть этого алгоритма состоит в следующем.

Сначала по заданной исходной схеме составляется матрица связей , в которой каждый элемент показывает количество связей между i-м и j-м модулями. После этого по специально выведенной формуле производится вычисление значений Sij - величин, показывающих изменение числа пересечений проводников при перестановке местами i-го и j-го модулей. Если Sij меньше или равно нулю, то перестановка считается нецелесообразной. Если жеSij - больше нуля, то перестановка считается целесообразной, i-й и j-й модули переставляются местами и вычисление значений Sрк для нового размещения модулей в позициях производится вновь и так до

123

тех пор, пока не наступит оптимизация, т. е. все значения Sрк будут отрицательными или равными нулю. Для достижения оптимизации часто бывает достаточно 2-4 перестановок, снижение числа пересечений проводников после оптимизации по сравнению с исходным происходит обычно в 1,5 - 10 раз.

Рассмотрим эту задачу математически и выведем формулу для вычисления значений величины Sij.

Пусть имеется какое-либо коммутационное поле с N установочными позициями для N модулей. Каждая позиция, а значит каждый

установленный в эту позицию модуль характеризуется двумя координатами xi и yi (рис.4.1).

Каждая пара модулей согласно электрической схеме имеет между собой mij соединений. Задача состоит в том, чтобы выбрать такое размещение модулей, которое было бы оптимальным в отношении принятого критерия оптимизации. В данной задаче в качестве критерия оптимизации примем число пересечений проводников.

Y
y3	А3	А4	Аi+2	АN
y2	А2	А5	Аi+1	АN-1
y1	А1	А6	Аi	АN-2
0	x1	x2	x3	x X

124

Задачу будем решать с помощью алгоритма парных перестановок . Для иллюстрации решения этой задачи представим схему в виде графа (рис. 4.2), в котором вершинами являются элементы (модули) схемы, а ребрами – соединения между элементами. Размещение позиций , в которые устанавливаются вершины графа, задается их координатами x и y, а соединения между элементами задаются матрицей связей (табл. 4.1).

	Матрица смежности.					Таблица 4.1
		1	2	3	4
1		0	0	1	1
2		0	0	1	1
3		1	1	0	1
4		1	1	1	0

Минимизацию числа пересечений графа можно провести методом парных перестановок его вершин. Этот метод можно проиллюстрировать следующим образом: пусть граф, представленный на рис. 4.2, имеет пересечение ребер.

4	3	1	3
	Рис.4. 2		Рис. 4.3

Рис.4.1.

125

Осуществим парную перестановку первой и четвертой вершин графа, в результате чего получим граф без пересечений

(рис. 4.3).

Общее количество пересечений для графа с n вершинами можно определить по формуле

	1	n	n n n
S			p[(i, j);(k, l)]mij mkl, (4.1)

	8 i 1		j 1 k 1 l 1

где n – число вершин графа;

1,если между ребом (i, j) и ребром (k,l) есть пересечение p[(i, j), (k,l)]

0, в противном случае;

mij, mkl - элементы матрицы смежности. В другой форме можно записать

n 1	n n 1	n
S p[(i, j);(k,l)]mij mkl . (4.2)
i 1	j i 1 k 1	l k 1

При парной перестановке вершин A и B могут исчезнуть только пересечения ребер, инцидентных этим вершинам, а число пересечений ребер, инцидентных неподвижным вершинам, не изменяется.

Пусть в некотором графе ребра, инцидентные вершине A, имеют следующее число пересечений с остальными ребрами графа:

n	n 1	n
SA		p[(A, j);(k,l)]mA jmkl, где j B.
j 1 k 1 l k 1
Аналогично, для вершины B
n	n 1	n
SB		p[(B, j);(k,l)]mB j mkl, где j A .

j 1 k 1 l k 1

126

После перестановки местами вершин A и B число пересечений изменится и станет равным

	n n 1		n
S'A			p[(A, j); (k, l)]mB jmkl, где j B .
	j 1 k 1 l k 1
S'	n n 1		n	p[(	B	, j);(k, l)]m	m	где j A .
B					B	A j	kl,
	j 1 k 1	l k 1

Тогда изменение числа пересечений в результате перестановки вершин A и B выразится формулой

S	AB	(S	A	S ) (S '		S ' )
	AB		A	B	A	B

n n 1 n

{p[(A, j);(k, l)] p[(B, j);(k, l)]} (mAj mBj) mkl ,

j 1 k 1 l k 1

где j A, j B.

Если SAB > 0, то перестановка вершин A и B целесообразна,

так как ведет к уменьшению числа пересечений. Определить наличие пересечений p[(i,j);(k,l)] между

ребрами (i,j) и (k,l) можно следующим образом в соответствии с рис.

4, 5.

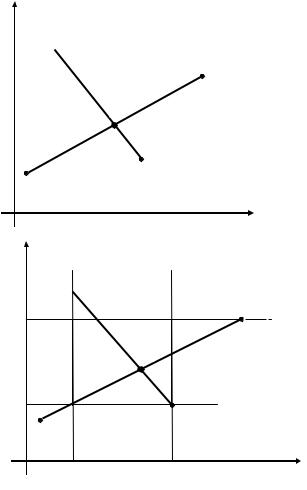
Ребра А1А2 и В1В2 являются отрезками прямых линий. Прямая линия описывается уравнением [2]:

y = kx + b.

Прямая, на которой лежит отрезок А1А2, описывается уравнением

				y = a1x+b1,
где	a	yA1 yA2	,	b y		a x		.
							A1
	1			1	A1	1

xA1 xA2

Аналогично для В1В2:

y = a2x+b2,

127

где

yB1 yB2

xB1 xB 2

2 B1

Точка Z пересечения этих прямых имеет координаты :

;

a1b2

a2b1

a1 a2

Необходимо далее определить, принадлежит ли точка

Z(x*,y*) обоим отрезкам А1А2, В1В2

в соответствии с рис. 5.3.

Если точка Z принадлежит заштрихованной области,

значит она принадлежит обоим отрезкам (рис. 5):

Z [A1,A2],

Z [B1,B2].

Следовательно, она является точкой пересечения

отрезков (A1,A2), (В1,В2), т.е.

Z = (A1,A2) (B1,B2),

хmin

– большее значение из двух минимальных

значений координаты х отрезков А1А2 и В1В2;

ymin

– большее значение из двух минимальных

значений координаты y отрезков А1А2 и В1В2;

хmax – меньшее значение из двух максимальных значений координат х отрезков А1А2 и В1В2;

ymax – меньшее значение из двух максимальных значений координат y отрезков А1А2 и В1В2.

Выполнение этого условия равноценно тому, что расстояние от обоих концов каждого отрезка до точки пересечения прямых меньше длины отрезка. Этот способ определения принадлежности точки пересечения отрезкам А1А2 и В1В2 был реализован в программе.

128

0	x
y	Рис. 4..4.

Рис. 4.5

Кроме такого общего случая расположения прямых на плоскости относительно координатных осей, возможны частные случаи

1. xA1 = xA2, xB1 xB2; (рис. 4.6) Тогда x* = xA1; y* = a2x*+b2,

			129
где a		yB1	yB2	, b		y	a	x	.
где a	2			, b	2	y	a	x	.
	2	xB1	xB 2		2	B1		2 B1
		xB1	xB 2

y		A
	B	A
	B

Рис. 4.6

2. xB1 = xB2, xA1 xA2;

Тогда x* = xB1; y* = a1x*+b1,

где a

yA1 yA2

, b

a x

xA1 xA2

3. yA1 = yA2, yB1 yB2.

Тогда y* = yA1; x*

y * b2

;

где a

yB1 yB2

, b

xB1 xB 2

4. yВ1 = yВ2, yA1 yA2.

Тогда y* = yB1; x*

y * b1

;

где a

yA1 yA2

, b

a x

xA1 xA2

5.xA1 = xA2,

130

, тогда x* = xA1, y* = yB1.

yB1 = yB2

6.xB1 = xB2,

, тогда x* = xB1, y* = yA1.

yA1 = yA2

7.xA1 = xA2,

xB1 = xB2 , тогда пересечение отсутствует.

xA1 xB1

8.yA1 = yA2,

yB1 = yB2 , тогда пересечение отсутствует.

yA1 yB1

9.к1 = к2,

,тогда пересечение отсутствует (рис. 4.7).

b1 b2.

10.xA1 = xA2, тогда оба отрезка находятся на xB1 = xB2, одной вертикальной прямой

xA1 = xB1

(рис. 8)

11.yA1 = yA2, тогда оба отрезка находятся на yB1 = yB2, одной горизонтальной прямой

yA1 = yB1

12. к1 = к2, , тогда оба отрезка находятся на одной наклонной

b1 = b2 прямой (рис. 9)

	131
y	A	y
	A	B
		B

b B

Рис4. 7

y B B A

b A

Рис. 4.9

Рис. 4.8 x

Для случаев 10, 11, 12, когда оба отрезка находятся на одной прямой, они могут иметь общие точки или не иметь их. Если отрезки имеют более одной общей точки, то будем считать отрезки условно пересекающимися. В таком случае при минимизации числа пересечений будет минимизироваться также число условно пересекающихся отрезков, что соответствует требованию: при разработке печатных плат

132

желательно иметь минимальное количество случаев наложения проводников друг на друга.

Для определения прохождения одного отрезка по другому с наличием более одной общей точки, кроме указанных в пунктах 10, 11, 12 условий, необходимо выполнение следующего условия: расстояние между самой дальней точкой одного отрезка и самой дальней точкой

Исследования проводились на различных схемах соединений с различным расположением установочных позиций для элементов с использованием 500 - 5000 исходных начальных размещений для каждой схемы.

Из многих рассмотренных примеров приведем следующий. Исходные данные:

количество элементов = 10; количество исходных начальных размещений: 500;

схема соединений представлена матрицей смежности (табл.

4.2);

Длины отрезков вычисляются по формуле d = |xi - xj| + |yi - yj|.

Все эти условия и ограничения были реализованы программно для оптимизации размещения элементов на коммутационном поле с минимизацией числа пересечений.

В качестве примера решения задачи минимизации числа пересечений при оптимизации размещения модулей на коммутационном поле с помощью ПЭВМ рассмотрим следующий.

Исходные данные: количество модулей = 10

схема соединений представлена матрицей смежности (табл.

координаты начального размещения модулей представлены в табл. 4.3.

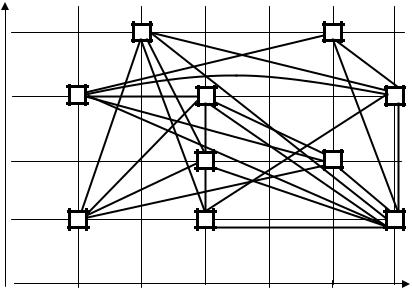
133

На рис. 4.10 показана схема соединений модулей, расположенных в исходных (до оптимизации) позициях с

числом пересечений 129.
			Таблица 4.2								Таблица 4.3				Таблица
	4.4
	1	2	3	4	5	6	7	8	9	1		x y		N	x y
										0
1	0	4	0	0	1	1	0	0	0	0		5	4	1	5	4

2	4	0	1	4	1	1	0	0	0	0		1	3	2	6	3

3	0	1	0	1	1	0	1	0	0	0		5	2	3	5	2

4	0	4	1	0	1	0	3	0	1	0		3	3	4	6	1

5	1	1	1	1	0	1	0	1	1	1		6	1	5	3	3

6	1	1	0	0	1	0	0	1	0	3		6	3	6	2	4

7	0	0	1	3	0	0	0	4	1	0		1	1	7	3	1

8	0	0	0	0	1	1	4	0	1	1		2	4	8	1	1

9	0	0	0	1	1	0	1	1	0	1		3	2	9	3	2

1	0	0	0	0	1	3	0	1	1	0		3	1	1	1	3

В результате решения этой задачи с помощью программы, реализующей алгоритм парных перестановок, получили новое (оптимальное) размещение модулей, указанное в табл. 4.4, с числом пересечений, равным 10 (локальный минимум; глобальный минимум, как будет показано в следующем разделе, равен 6). До оптимизации число пересечений было равно 129, то есть число пересечений уменьшилось после оптимизации почти в 13 раз. Схема соединений модулей, расположенных в позициях, после оптимизации показана на рис. 4.11 . На рис. 10 и 11 цифра у линии показывает число соединений между модулями. Цифра 1 не проставляется.

134

4.2.2. Исследование зависимости эффективности алгоритма парных перестановок от исходных начальных размещений и способы повышения его эффективности

Одним из методов оптимизации размещения элементов с минимизацией числа пересечений является алгоритм парных перестановок [1]. Согласно этому алгоритму сначала все элементы схемы произвольным образом размещаются по заданному количеству установочных позиций, а затем производятся перестановки тех пар элементов, находящихся в разных позициях, которые дают уменьшение числа пересечений трасс.

Y
4		8
3	2	4

	4
2	3
2

0	1	2		3	4	5		X

Рис. 10. Схема соединений модулей

135

В результате таких перестановок достигается локальный минимум. Близость его к глобальному минимуму, т.е. степень оптимизации, существенно зависит от исходного начального (обычно произвольного) размещения элементов в позициях. В связи с этим целесообразно исследовать зависимость степени оптимизации от начальных размещений.

Для этого необходимо разработать программу, реализующую алгоритм парных перестановок с использованием большого количества начальных размещений. Для облегчения обработки статистических данных в программе следует предусмотреть вывод результатов оптимизации в порядке уменьшения степени оптимизации с указанием количества появлений каждого оптимума. Отдельно вывести наилучший оптимум с указанием размещения элементов по позициям. Для оценки

Y
4		2
		2
		4
3	4
3
2	3
	3
1	7	4
	7	4

0	1	2	3	4	5	X
			Рис. 4.11

		136
Результаты эксперимента и их обработка					Таблица 5
Но	Значен	Количе	Вероятн	Удалени		Сумм
мер	ие	ство	ость Pi	е		арная
мин	миниму	появле	Появлен	миниму		вероятность
иму	ма	ний	ия	ма от		Pi
ма	числа	миниму	миниму	глобаль
	пересеч	ма	ма	ного ,
	ений			%
1	6	14	0,028	0		0,028
2	7	22	0,044	16,6		0,072
3	8	89	0,178	33,3		0,250
4	9	12	0,024	50,0		0,274
5	10	43	0,086	66,6		0,360
6	11	31	0,062	83,3		0,422
7	12	22	0,044	100,0		0,466
8	13	40	0,080	116,6		0,546
9	14	65	0,130	133,3		0,676
10	15	39	0,078	150,0		0,754
11	16	18	0,036	166,6		0,790
12	17	29	0,058	183,3		0,848
13	18	11	0,022	200,0		0,870
14	19	25	0,050	216,6		0,920
15	20	7	0,014	233,3		0,934
16	21	12	0,024	250,0		0,958
17	22	3	0,006	266,6		0,964
18	23	2	0,004	283,3		0,968
19	24	5	0,010	300,0		0,978
20	25	4	0,008	316,6		0,986
21	26	3	0,006	333,3		0,992
22	27	2	0,004	350,0		0,996
23	29	1	0,002	366,6		0,998

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
30.04.20221.24 Mб16Учебное пособие 1487.pdf
#
30.04.20221.24 Mб5Учебное пособие 1488.pdf
#
30.04.20221.24 Mб7Учебное пособие 1489.pdf
#
30.04.2022302.13 Кб2Учебное пособие 149.pdf
#
30.04.20221.24 Mб41Учебное пособие 1490.pdf
#
30.04.20221.24 Mб9Учебное пособие 1491.pdf
#
30.04.20221.24 Mб5Учебное пособие 1492.pdf
#
30.04.20221.24 Mб3Учебное пособие 1493.pdf
#
30.04.20221.25 Mб2Учебное пособие 1494.pdf
#
30.04.20221.25 Mб6Учебное пособие 1495.pdf
#
30.04.20221.25 Mб17Учебное пособие 1496.pdf